-
Chương 1: Số hữu tỉ
-
Chương 2: Số thực
-
Chương 3: Góc và đường thẳng song song
-
Chương 4: Tam giác bằng nhau
-
Chương 5: Thu thập và biểu diễn dữ liệu
-
Chương 6: Tỉ lệ thức và đại lượng tỉ lệ
-
Chương 7: Biểu thức đại số và đa thức một biến
-
Chương 8: Làm quen với biến cố và xác suất
-
Chương 9: Quan hệ giữa các yếu tố trong một tam giác
- Bài 31: Quan hệ giữa góc và cạnh đối diện trong một tam giác
- Bài 32: Quan hệ đường vuông góc và đường xiên
- Bài 33: Quan hệ giữa ba cạnh trong một tam giác
- Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
- Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác
-
Chương 10: Một số hình khối trong thực tiễn
Trắc nghiệm Bài 12: Tổng các góc trong một tam giác Toán 7 Kết nối tri thức
Đề bài
-
A.
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
-
B.
\(\widehat {CAD} + \widehat {BAD} + \widehat {BAC} = 180^\circ \)
-
C.
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
-
D.
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
-
A.
\({32^0}\)
-
B.
\({35^0}\)
-
C.
\(24^\circ \)
-
D.
\({90^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({100^0}\)
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
-
A.
\(\widehat B = {65^0},\widehat C = {15^0}\)
-
B.
\(\widehat B = {75^0},\widehat C = {25^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
-
A.
60\(^\circ \)
-
B.
90\(^\circ \)
-
C.
120\(^\circ \)
-
D.
30\(^\circ \)
Khẳng định nào sau đây là sai?
-
A.
Tam giác tù là tam giác có 1 góc tù
-
B.
Tam giác nhọn là tam giác có 3 góc đều là góc nhọn
-
C.
Góc lớn nhất trong 1 tam giác là góc tù
-
D.
2 góc nhọn trong tam giác vuông phụ nhau.
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó
-
A.
\(\widehat B + \widehat C = 90^\circ \)
-
B.
\(\widehat B + \widehat C = 180^\circ \)
-
C.
\(\widehat B + \widehat C = 100^\circ \)
-
D.
\(\widehat B + \widehat C = 60^\circ \)
Cho tam giác $ABC$ có \(\widehat A = {96^0},\widehat C = {50^0}\). Số đo góc $B$ là:
-
A.
\({34^0}\)
-
B.
\({35^0}\)
-
C.
\({60^0}\)
-
D.
\({90^0}\)
Cho hình vẽ sau. Tính số đo \(x.\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({49^0}\)
-
D.
\({98^0}\)
Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc .
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({49^0}\)
-
D.
\({60^0}\)
Cho hình sau. Tính số đo $x.$
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({140^0}\)
Cho tam giác \(ABC\) biết rằng số đo các góc $\widehat A;\widehat B;\widehat C$ tỉ lệ với $2;\,\,3;\,\,4$. Tính \(\widehat B.\)
-
A.
\(\widehat B = {60^0}\)
-
B.
\(\widehat B = {90^0}\)
-
C.
\(\widehat B = {40^0}\)
-
D.
\(\widehat B = {80^0}\)
Tam giác $ABC$ có $\widehat A = {100^0},\widehat B - \widehat C = {40^0}$. Số đo góc $B$ và góc $C$ lần lượt là:
-
A.
\(\widehat B = {60^0},\widehat C = {20^0}\)
-
B.
\(\widehat B = {20^0},\widehat C = {60^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
Cho tam giác $ABC$ có $\widehat A = {50^0},\widehat B = {70^0}.$ Tia phân giác của góc C cắt cạnh AB tại M. Tính \(\widehat {AMC}\) và \(\widehat {BMC}.\)
-
A.
\(\widehat {AMC} = 120^\circ ;\,\widehat {BMC} = 60^\circ .\)
-
B.
\(\widehat {AMC} = 80^\circ ;\,\widehat {BMC} = 100^\circ .\)
-
C.
\(\widehat {AMC} = 110^\circ ;\,\widehat {BMC} = 70^\circ .\)
-
D.
\(\widehat {AMC} = 100^\circ ;\,\widehat {BMC} = 80^\circ .\)
Cho tam giác ABC có \(\widehat B = {80^0},3\widehat A = 2\widehat C.\)Tính \(\widehat A\) và \(\widehat C?\)
-
A.
\(\widehat A = 60^\circ ;\,\widehat C = 40^\circ .\)
-
B.
\(\widehat A = 30^\circ ;\,\widehat C = 50^\circ .\)
-
C.
\(\widehat A = 40^\circ ;\,\widehat C = 60^\circ .\)
-
D.
\(\widehat A = 40^\circ ;\,\widehat C = 30^\circ .\)
Cho hình vẽ sau. Tính số đo góc $x?$
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC ở E.
Chọn câu sai.
-
A.
\(\widehat {BEC} > {90^0}\)
-
B.
\(\widehat {BEC} < {90^0}\)
-
C.
\(\widehat {BEC} > \widehat {EBA}\)
-
D.
\(\widehat {BEC} > \widehat {ECB}\)
\(\widehat C - \widehat B = {26^0}\). Tính \(\widehat {AEB}\) và $\widehat {BEC}$.
-
A.
\(\widehat {AEB} = 70^\circ ;\,\widehat {BEC} = 110^\circ .\)
-
B.
\(\widehat {AEB} = 106^\circ ;\,\widehat {BEC} = 74^\circ .\)
-
C.
\(\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .\)
-
D.
\(\widehat {AEB} = 60^\circ ;\,\widehat {BEC} = 120^\circ .\)
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo $\widehat {ADC}$ biết rằng: \(\widehat B - \widehat C = {20^0}.\)
-
A.
\({80^o}\)
-
B.
\( {110^o}\)
-
C.
\({100^o}\)
-
D.
\({105^o}\)
Lời giải và đáp án
-
A.
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
-
B.
\(\widehat {CAD} + \widehat {BAD} + \widehat {BAC} = 180^\circ \)
-
C.
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
-
D.
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Đáp án : B
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ
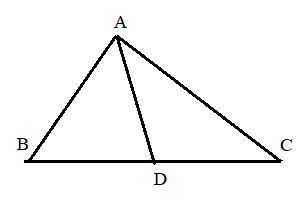
Áp dụng định lí tổng số đo 3 góc trong 3 tam giác ABD, ACD và ABC, ta được:
\(\widehat {BAD} + \widehat {ABD} + \widehat {ADB} = 180^\circ \)
\(\widehat {CAD} + \widehat {ADC} + \widehat {ACB} = 180^\circ \)
\(\widehat {BAC} + \widehat {ACD} + \widehat {ABD} = 180^\circ \)
Vậy A,C,D đúng
Cho tam giác ABC có \(\widehat A = 86^\circ ;\widehat B = 62^\circ \). Số đo góc C là:
-
A.
\({32^0}\)
-
B.
\({35^0}\)
-
C.
\(24^\circ \)
-
D.
\({90^0}\)
Đáp án : A
Tổng số đo 3 góc trong 1 tam giác bằng 180 độ
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = 180^\circ \\ \Rightarrow 86^\circ + 62^\circ + \widehat C = 180^\circ \\ \Rightarrow \widehat C = 180^\circ - 86^\circ - 62^\circ = 32^\circ \end{array}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({100^0}\)
Đáp án : B
Áp dụng tính chất tổng ba góc của một tam giác: Trong \(\Delta ABC:\,\widehat A + \widehat B + \widehat C = {180^0}.\)
Áp dụng tính chất tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = {180^0}\)
Suy ra \(\widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {80^0} = {100^0}\).
Hay \(x + x = {100^0}\) hay \( 2x = {100^0} \) suy ra \( x = {50^0}\)
Cho tam giác ABC có \(\widehat A = {50^0},\widehat B = {70^0}\). Tia phân giác của góc C cắt cạnh AB tại M. Số đo góc BMC là:
-
A.
\({50^0}\)
-
B.
\(80^\circ \)
-
C.
\({100^0}\)
-
D.
\({90^0}\)
Đáp án : B
Áp dụng tính chất tổng ba góc của một tam giác, tính chất tia phân giác của một góc.
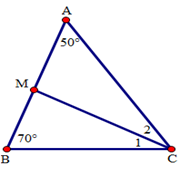
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat C = {180^0} - \left( {\widehat A + \widehat B} \right) = {180^0} - \left( {{{50}^0} + {{70}^0}} \right) = {60^0}\).
Do CM là tia phân giác của góc ACB nên \(\widehat {{C_1}} = \widehat {{C_2}} = \frac{{\widehat C}}{2} = \frac{{{{60}^0}}}{2} = {30^0}\).
Áp dụng định lí tổng ba góc trong tam giác BMC có:
\(\widehat B + \widehat {BMC} + {\widehat C_1} = {180^0} \Rightarrow \widehat {BMC} = {180^0} - \left( {\widehat B + \widehat {{C_1}}} \right) = {180^0} - \left( {{{70}^0} + {{30}^0}} \right) = {80^0}\)
Tam giác ABC có \(\widehat A = {80^0},\widehat B - \widehat C = {50^0}\). Số đo góc B và góc C lần lượt là:
-
A.
\(\widehat B = {65^0},\widehat C = {15^0}\)
-
B.
\(\widehat B = {75^0},\widehat C = {25^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
Đáp án : B
+ Áp dụng tính chất tổng ba góc của một tam giác, tính tổng 2 góc B và C
+ Bài toán trở về tìm 2 số biết tổng và hiệu của chúng
Áp dụng định lí tổng ba góc trong tam giác ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat B + \widehat C = 180^\circ - 80^\circ = 100^\circ \)
Ta có:
\(\begin{array}{l}\widehat C = (100^\circ - 50^\circ ):2 = 25^\circ ;\\\widehat B = \widehat C + 50^\circ = 25^\circ + 50^\circ = 75^\circ \end{array}\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Đáp án : C
Áp dụng tính chất tổng ba góc của một tam giác
Áp dụng tính chất tổng ba góc trong tam giác ACF có :\(\widehat A + \widehat {ACF} + \widehat {AFC} = {180^0} \Leftrightarrow {60^0} + \widehat {ACF} + {90^0} = {180^0}\)
\( \Rightarrow \widehat {ACF} = {180^0} - {60^0} - {90^0} = {30^0}.\)
Áp dụng tính chất tổng ba góc trong \(\Delta IEC\) ta có: \(\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = {180^0} \Leftrightarrow {30^0} + x + {90^0} = {180^0}\)
\( \Rightarrow x = {180^0} - {30^0} - {90^0} = {60^0}.\)
Cho hai đoạn thẳng AB và CD cắt nhau ở E. Các tia phân giác của các góc ACE và DBE cắt nhau ở K. Tính số đo góc BKC?
-
A.
90\(^\circ \)
-
B.
\(\widehat {BDC} - \widehat {BAC}\)
-
C.
\(\frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
-
D.
\(\widehat {BDC} + \widehat {BAC}\)
Đáp án : C
Áp dụng tính chất tổng ba góc của một tam giác
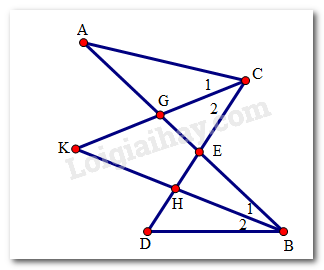
Gọi G là giao điểm của CK và AE, H là giao điểm của BK và DE.
Xét tam giác KGB và tam giác AGC và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{B_1}} = \widehat {AGK}\\\widehat A + \widehat {{C_1}} = \widehat {AGK}\end{array} \right. \Rightarrow \widehat K + \widehat {{B_1}} = \widehat A + \widehat {{C_1}}\) (1)
Xét tam giác KHC và tam giác DHB và theo tính chất góc ngoài của tam giác ta có:\(\left\{ \begin{array}{l}\widehat K + \widehat {{C_2}} = \widehat {EHB}\\\widehat D + \widehat {{B_2}} = \widehat {EHB}\end{array} \right. \Rightarrow \widehat K + \widehat {{C_2}} = \widehat D + \widehat {{B_2}}\) (2)
Do \(\widehat {{B_1}} = \widehat {{B_2}}\) (BK là tia phân giác của góc DBA);
\(\widehat {{C_1}} = \widehat {{C_2}}\) ( CK là tia phân giác của góc ACD).
Nên cộng (1) với (2) ta được \(2\widehat K = \widehat A + \widehat D\), do đó \(\widehat K = \frac{{\widehat A + \widehat D}}{2}\) hay \(\widehat {BKC} = \frac{{\widehat {BAC} + \widehat {BDC}}}{2}\)
Tam giác ABC có \(\widehat B + \widehat C = \widehat A\) và \(\widehat C = 2\widehat B\). Tia phân giác của góc C cắt AB ở D. Tính \(\widehat {ADC}\)
-
A.
60\(^\circ \)
-
B.
90\(^\circ \)
-
C.
120\(^\circ \)
-
D.
30\(^\circ \)
Đáp án : A
Sử dụng tính chất tổng các góc của một tam giác, tính chất tia phân giác của một góc
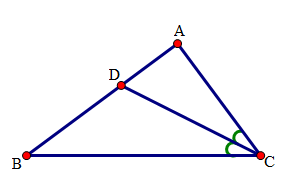
Xét tam giác ABC có \(\widehat A + \widehat B + \widehat C = {180^0}\) mà \(\widehat B + \widehat C = \widehat A\), do đó \(2\widehat A = {180^0} \Rightarrow \widehat A = {90^0}\).
Trong tam giác ABC do \(\widehat A = {90^0}\) nên \(\widehat B + \widehat C = {90^ \circ }\). Mà \(\widehat C = 2\widehat B\) do đó \(3\widehat B = {90^0} \Rightarrow \widehat B = {30^0}\)nên \(\widehat C = {60^0}\)
Do CD là tia phân giác của góc ACD nên \(\widehat {ACD} = \widehat {DCB} = \widehat C:2 = {60^ \circ }:2 = {30^ \circ }\)
Xét tam giác ADC có: \(\widehat A + \widehat {ADC} + \widehat {ACD} = {180^0} \Rightarrow \widehat {ADC} = {180^0} - \left( {\widehat A + \widehat {ACD}} \right) = {180^0} - \left( {{{30}^0} + {{90}^ \circ }} \right) = {60^ \circ }\)
Khẳng định nào sau đây là sai?
-
A.
Tam giác tù là tam giác có 1 góc tù
-
B.
Tam giác nhọn là tam giác có 3 góc đều là góc nhọn
-
C.
Góc lớn nhất trong 1 tam giác là góc tù
-
D.
2 góc nhọn trong tam giác vuông phụ nhau.
Đáp án : C
Lý thuyết về 3 loại tam giác: Tam giác tù, tam giác vuông, tam giác nhọn
Các khẳng định A,B,D đúng.
Khẳng định C sai vì: Góc lớn nhất trong tam giác nhọn là một góc nhọn, góc lớn nhất trong tam giác vuông là góc vuông. Do đó không thể khẳng định góc lớn nhất trong tam giác là góc tù.
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({130^0}\)
Đáp án : D
Góc ngoài tam giác bằng tổng 2 góc trong không kề với nó.
Ta có góc cần tính là góc ngoài tại đỉnh C của tam giác ABC nên:
\(x = \widehat A + \widehat B = 90^\circ + 40^\circ = 130^\circ \)
Cho tam giác \(ABC\) vuông tại \(A\). Khi đó
-
A.
\(\widehat B + \widehat C = 90^\circ \)
-
B.
\(\widehat B + \widehat C = 180^\circ \)
-
C.
\(\widehat B + \widehat C = 100^\circ \)
-
D.
\(\widehat B + \widehat C = 60^\circ \)
Đáp án : A
Áp dụng tính chất tam giác vuông: Trong tam giác vuông, hai góc nhọn phụ nhau.
Vì tam giác \(ABC\) vuông tại \(A\) nên \(\widehat B + \widehat C = 90^\circ \).
Cho tam giác $ABC$ có \(\widehat A = {96^0},\widehat C = {50^0}\). Số đo góc $B$ là:
-
A.
\({34^0}\)
-
B.
\({35^0}\)
-
C.
\({60^0}\)
-
D.
\({90^0}\)
Đáp án : A
Áp dụng tính chất tổng ba góc của một tam giác: \(Trong\,\,\Delta ABC:\,\,\,\,\widehat A + \widehat B + \widehat C = {180^0}.\)
Xét tam giác $ABC$ có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B = {180^0} - \left( {\widehat A + \widehat C} \right) = {180^0} - \left( {{{96}^0} + {{50}^0}} \right) = {34^0}$.
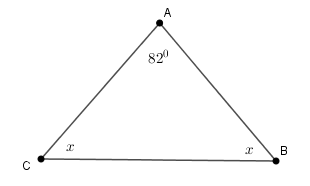
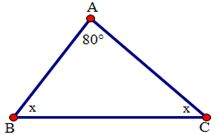
Cho hình vẽ sau. Tính số đo \(x.\)
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({49^0}\)
-
D.
\({98^0}\)
Đáp án : C
Áp dụng tính chất tổng ba góc của một tam giác: \(Trong\,\,\Delta ABC:\,\,\,\,\widehat A + \widehat B + \widehat C = {180^0}.\)
Xét tam giác $ABC$ có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B + \widehat C = {180^0} - \widehat A = {180^0} - {82^0} = {98^0}$.
Hay \(x + x = {98^0} \Rightarrow 2x = {98^0} \Rightarrow x = {49^0}\)
Cho tam giác có ba góc bằng nhau. Tính số đo mỗi góc .
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({49^0}\)
-
D.
\({60^0}\)
Đáp án : D
Áp dụng tính chất tổng ba góc của một tam giác: \(Trong\,\,\Delta ABC:\,\,\,\,\widehat A + \widehat B + \widehat C = {180^0}.\)
Giả sử tam giác \(ABC\) có ba góc bằng nhau \(\widehat A = \widehat B = \widehat C\)
Lại có \(\widehat A + \widehat B + \widehat C = {180^0}\)\( \Rightarrow \widehat A + \widehat A + \widehat A = 180^\circ \Rightarrow 3\widehat A = 180^\circ \)\( \Rightarrow \widehat A = 180^\circ :3\)\( \Rightarrow \widehat A = 60^\circ .\)
Vậy \(\widehat A = \widehat B = \widehat C = 60^\circ .\)
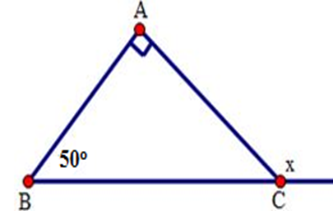
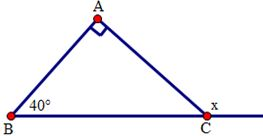
Cho hình sau. Tính số đo $x.$
-
A.
\({90^0}\)
-
B.
\({100^0}\)
-
C.
\({120^0}\)
-
D.
\({140^0}\)
Đáp án : D
Áp dụng tính chất góc ngoài của tam giác: Góc ngoài của tam giác bẳng tổng hai góc trong không kề với nó.
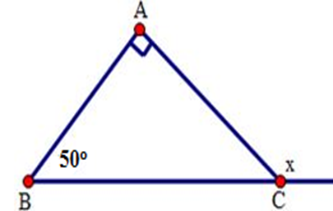
Ta có $x$ là số đo góc ngoài tại đỉnh $C$ của tam giác $ABC$ nên
\(x = \widehat A + \widehat B = {50^0} + {90^0} = {140^0}\).
Cho tam giác \(ABC\) biết rằng số đo các góc $\widehat A;\widehat B;\widehat C$ tỉ lệ với $2;\,\,3;\,\,4$. Tính \(\widehat B.\)
-
A.
\(\widehat B = {60^0}\)
-
B.
\(\widehat B = {90^0}\)
-
C.
\(\widehat B = {40^0}\)
-
D.
\(\widehat B = {80^0}\)
Đáp án : A
+) Áp dụng tính chất tổng ba góc trong một tam giác.
+) Sử dụng tính chất của dãy tỉ số bằng nhau ta tính ra số đo các góc của tam giác.
\(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{e}{f} = \dfrac{{a + c + e}}{{d + d + f}}.\)
Theo tính chất tổng 3 góc của tam giác ta có: \(\widehat A + \widehat B + \widehat C = {180^0}.\)
Theo đề bài ta có: \(\widehat A:\widehat B:\widehat C = 2:3:4 \Rightarrow \dfrac{{\widehat A}}{2} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{4}.\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\begin{array}{l}\dfrac{{\widehat A}}{2} = \dfrac{{\widehat B}}{3} = \dfrac{{\widehat C}}{4} = \dfrac{{\widehat A + \widehat B + \widehat C}}{{2 + 3 + 4}} \\= \dfrac{{{{180}^0}}}{9} = {20^0}.\\ \Rightarrow \left\{ \begin{array}{l}\widehat A = {20^0}.2 = {40^0}\\\widehat B = {20^0}.3 = {60^0}\\\widehat C = {20^0}.4 = {80^0}\end{array} \right..\end{array}\)
Vậy các góc của tam giác ABC là: \(\widehat A = {40^0};\,\,\widehat B = {60^0};\,\,\widehat C = {80^0}.\)
Tam giác $ABC$ có $\widehat A = {100^0},\widehat B - \widehat C = {40^0}$. Số đo góc $B$ và góc $C$ lần lượt là:
-
A.
\(\widehat B = {60^0},\widehat C = {20^0}\)
-
B.
\(\widehat B = {20^0},\widehat C = {60^0}\)
-
C.
\(\widehat B = {70^0},\widehat C = {20^0}\)
-
D.
\(\widehat B = {80^0},\widehat C = {30^0}\)
Đáp án : A
Áp dụng tính chất tổng ba góc của một tam giác, kết hợp với giả thiết của đề bài để tìm ra số đo góc $B$ và $C.$
Xét tam giác $ABC$ có :$\widehat A + \widehat B + \widehat C = {180^0} \Rightarrow \widehat B + \widehat C = {180^0} - {100^0} = {80^0}$(1)
Theo đề bài ta có:$\widehat B - \widehat C = {40^0}$ (2)
Từ (1) ta có: \(\widehat C = {80^0} - \widehat B.\)
Thế vào (2) ta được: \(\widehat B - \left( {{{80}^0} - \widehat B} \right) = {40^0} \Leftrightarrow 2.\widehat B = {40^0} + {80^0} \Leftrightarrow \widehat B = \dfrac{{{{120}^0}}}{2} = {60^0}.\)
\( \Rightarrow \widehat C = {80^0} - {60^0} = {20^0}.\)
Cho tam giác $ABC$ có $\widehat A = {50^0},\widehat B = {70^0}.$ Tia phân giác của góc C cắt cạnh AB tại M. Tính \(\widehat {AMC}\) và \(\widehat {BMC}.\)
-
A.
\(\widehat {AMC} = 120^\circ ;\,\widehat {BMC} = 60^\circ .\)
-
B.
\(\widehat {AMC} = 80^\circ ;\,\widehat {BMC} = 100^\circ .\)
-
C.
\(\widehat {AMC} = 110^\circ ;\,\widehat {BMC} = 70^\circ .\)
-
D.
\(\widehat {AMC} = 100^\circ ;\,\widehat {BMC} = 80^\circ .\)
Đáp án : D
+ Tính góc \(C\) dựa vào định lý tổng ba góc trong tam giác. Từ đó sử dụng tính chất tia phân giác để tính \(\widehat {BCM}.\)
+ Tính góc \(\widehat {AMC}\) và \(\widehat {BMC}\) dựa vào tính chất góc ngoài của tam giác và hai góc kề bù.
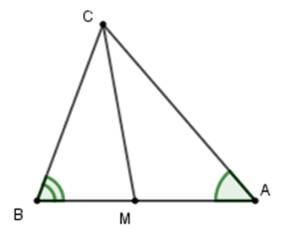
Xét tam giác \(ABC\) có \(\widehat A + \widehat B + \widehat {BCA} = 180^\circ \)(định lý tổng ba góc trong tam giác) mà $\widehat A = {50^0},\widehat B = {70^0}.$ Suy ra \(\widehat {BCA} = 180^\circ - 50^\circ - 70^\circ = 60^\circ .\)
Vì \(CM\) là tia phân giác của góc \(BCA\) nên \(\widehat {BCM} = \widehat {ACM} = \dfrac{{\widehat {BCA}}}{2} = \dfrac{{60^\circ }}{2} = 30^\circ \)
Ta có \(\widehat {AMC}\) là góc ngoài tại đỉnh \(M\) của tam giác \(BCM\) nên ta có
\(\widehat {AMC} = \widehat B + \widehat {BCM} = 70^\circ + 30^\circ = 100^\circ \)
Lại có \(\widehat {AMC} + \widehat {BMC} = 180^\circ \) (hai góc kề bù) suy ra \(\widehat {BMC} = 180^\circ - \widehat {AMC} = 80^\circ .\)
Vậy \(\widehat {AMC} = 100^\circ ;\,\widehat {BMC} = 80^\circ .\)
Cho tam giác ABC có \(\widehat B = {80^0},3\widehat A = 2\widehat C.\)Tính \(\widehat A\) và \(\widehat C?\)
-
A.
\(\widehat A = 60^\circ ;\,\widehat C = 40^\circ .\)
-
B.
\(\widehat A = 30^\circ ;\,\widehat C = 50^\circ .\)
-
C.
\(\widehat A = 40^\circ ;\,\widehat C = 60^\circ .\)
-
D.
\(\widehat A = 40^\circ ;\,\widehat C = 30^\circ .\)
Đáp án : C
+ Sử dụng định lý tổng ba góc trong tam giác.
+ Sử dụng tính chất dãy tỉ số bằng nhau: \(\dfrac{a}{b} = \dfrac{c}{d} = \dfrac{{a + c}}{{b + d}}.\)
Xét tam giác $ABC$ có \(\widehat B = {80^0}.\) Theo định lý về tổng ba góc trong tam giác ta có
\(\widehat A + \widehat B + \widehat C = 180^\circ \Rightarrow \widehat A + \widehat C = 180^\circ - \widehat B\)\( \Rightarrow \widehat A + \widehat C = 100^\circ .\)
Lại có \(3\widehat A = 2\widehat C \Rightarrow \dfrac{{\widehat A}}{2} = \dfrac{{\widehat C}}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được
\(\dfrac{{\widehat A}}{2} = \dfrac{{\widehat C}}{3} = \dfrac{{\widehat A + \widehat C}}{{2 + 3}} = \dfrac{{100^\circ }}{5} = 20^\circ \)
Suy ra \(\widehat A = 40^\circ ;\,\widehat C = 60^\circ .\)
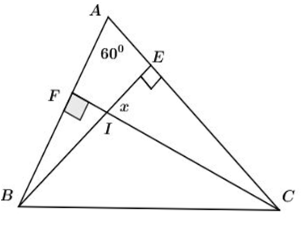
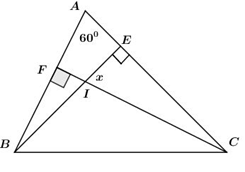
Cho hình vẽ sau. Tính số đo góc $x?$
-
A.
\({40^0}\)
-
B.
\({50^0}\)
-
C.
\({60^0}\)
-
D.
\({70^0}\)
Đáp án : C
Áp dụng tính chất tổng ba góc trong một tam giác.
Xét tam giác $ACF$ có :$\widehat A + \widehat {ACF} + \widehat {AFC} = {180^0} \Leftrightarrow {60^0} + \widehat {ACF} + {90^0} = {180^0}$
\( \Rightarrow \widehat {ACF} = {180^0} - {60^0} - {90^0} = {30^0}.\)
Xét \(\Delta IEC\) ta có: \(\widehat {IEC} + \widehat {ECI} + \widehat {EIC} = {180^0} \Leftrightarrow {30^0} + x + {90^0} = {180^0}\)
\( \Rightarrow x = {180^0} - {30^0} - {90^0} = {60^0}.\)
Cho tam giác ABC vuông ở A. Tia phân giác của góc B cắt AC ở E.
Chọn câu sai.
-
A.
\(\widehat {BEC} > {90^0}\)
-
B.
\(\widehat {BEC} < {90^0}\)
-
C.
\(\widehat {BEC} > \widehat {EBA}\)
-
D.
\(\widehat {BEC} > \widehat {ECB}\)
Đáp án: B
Sử dụng tính chất góc ngoài của tam giác, tính chất tổng ba góc của tam giác.
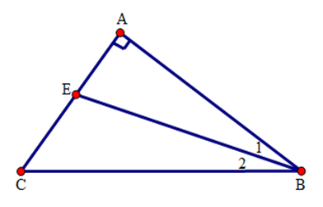
Góc $BEC$ là góc ngoài ở đỉnh $E$ của tam giác $AEC$ nên \(\widehat {BEC} = \widehat A + \widehat {ABE} = {90^ \circ } + \widehat {ABE} > {90^ \circ }\)
Vậy góc $BEC$ là góc tù nên \(\widehat {BEC} > \widehat {EBA}\) và \(\widehat {BEC} > \widehat {ECB}.\)
Vậy A, C, D đúng, B sai.
\(\widehat C - \widehat B = {26^0}\). Tính \(\widehat {AEB}\) và $\widehat {BEC}$.
-
A.
\(\widehat {AEB} = 70^\circ ;\,\widehat {BEC} = 110^\circ .\)
-
B.
\(\widehat {AEB} = 106^\circ ;\,\widehat {BEC} = 74^\circ .\)
-
C.
\(\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .\)
-
D.
\(\widehat {AEB} = 60^\circ ;\,\widehat {BEC} = 120^\circ .\)
Đáp án: C
Sử dụng tính chất góc ngoài của tam giác, tính chất tổng ba góc của tam giác.
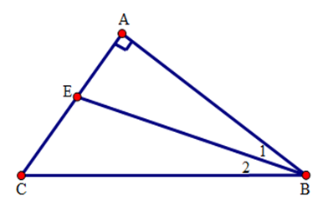
Theo giả thiết \(\widehat C - \widehat B = {26^0}\).
Mặt khác do tam giác $ABC$ vuông tại $A$ nên \(\widehat B + \widehat C = {90^ \circ }\)
Từ đó ta có \(\widehat C = \dfrac{{90^\circ + 26^\circ }}{2} = {58^0} \Rightarrow \widehat B = {32^0}\).
Do $BE$ là tia phân giác của góc $ABC$ nên \(\widehat {{B_1}} = \widehat {{B_2}} = {16^0}\)
Sử dụng tinh chất góc ngoài của tam giác ta tìm được \(\widehat {AEB} = \widehat C + \widehat {{B_2}} = {58^0} + 16^\circ = 74^\circ .\)
Và \(\widehat {BEC} = \widehat A + \widehat {{B_1}} = 106^\circ .\)
Vậy \(\widehat {AEB} = 74^\circ ;\,\widehat {BEC} = 106^\circ .\)
Cho tam giác ABC. Tia phân giác của góc A cắt BC tại D. Tính số đo $\widehat {ADC}$ biết rằng: \(\widehat B - \widehat C = {20^0}.\)
-
A.
\({80^o}\)
-
B.
\( {110^o}\)
-
C.
\({100^o}\)
-
D.
\({105^o}\)
Đáp án : C
- Áp dụng định lí: Góc ngoài tam giác bằng tổng hai góc trong không kề với nó.
- Tính chất: Hai góc kề bù có tống số đo bằng \({180^o}.\)
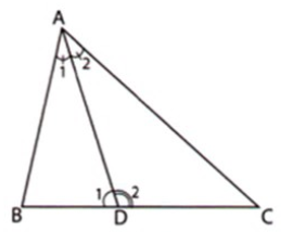
Ta có: \(\widehat {{D_2}}\) là góc ngoài tại đỉnh \(D\) của tam giác \(ABD\) nên \(\widehat {{D_2}} = \widehat {{A_1}} + \widehat B\,\,\,\,\,(1)\)
Ta có: \(\widehat {{D_1}}\) là góc ngoài tại đỉnh \(D\) của tam giác \(ADC\) nên \(\widehat {{D_1}} = \widehat {{A_2}} + \widehat C\,\,\,\,\,\,(2)\)
Từ (1) và (2) ta có:
\(\widehat {{D_2}} - \widehat {{D_1}} = \widehat {{A_1}} - \widehat {{A_2}} + \widehat B - \widehat C = \left( {\widehat {{A_1}} - \widehat {{A_2}}} \right) + \left( {\widehat B - \widehat C} \right)\)
Vì \(AD\) là tia phân giác \(\widehat A\) nên \(\widehat {{A_1}} = \widehat {{A_2}}\) và \(\widehat B - \widehat C = {20^0}\,\,(gt)\) suy ra \(\widehat {{D_2}} - \widehat {{D_1}} = {20^o}\,\,\,\,\,\,(3)\)
Mặt khác \(\widehat {{D_1}}\) và \(\widehat {{D_2}}\) là hai góc kề bù nên \(\widehat {{D_1}} + \widehat {{D_2}} = {180^o}\,\,\,\,\,(4)\)
Từ (3) và (4) suy ra \(\widehat {{D_2}} = \left( {{{20}^o} + {{180}^o}} \right):2 = {100^o};\,\,\widehat {{D_1}} = {180^o} - {100^o} = {80^o}.\)
Vậy \(\widehat {{D_1}} = {80^o};\,\widehat {{D_2}} = {100^o}.\)
Luyện tập và củng cố kiến thức Bài 13: Hai tam giác bằng nhau. Trường hợp bằng nhau thứ nhất của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 14: Trường hợp bằng nhau thứ hai và thứ ba của tam giác Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 15: Các trường hợp bằng nhau của tam giác vuông Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 16: Tam giác cân. Đường trung trực của đoạn thẳng Toán 7 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
- Trắc nghiệm Bài 37: Hình lăng trụ đứng tam giác và hình lăng trụ đứng tứ giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 36: Hình hộp chữ nhật và hình lập phương Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 35: Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác Toán 7 Kết nối tri thức
- Trắc nghiệm Bài 33: Quan hệ giữa ba cạnh trong một tam giác Toán 7 Kết nối tri thức
