Trắc nghiệm Các dạng toán về bội chung và bội chung nhỏ nhất Toán 6 Cánh diều
Đề bài
Chọn câu trả lời sai.
-
A.
${\rm{5}} \in $ ƯC\(\left( {55;110} \right)\)
-
B.
$24 \in BC\left( {3;4} \right)$
-
C.
$10 \notin $ ƯC\(\left( {55;110} \right)\)
-
D.
$12 = BC\left( {3;4} \right)$
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông
thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ
200 đến 300 bông.
-
A.
210
-
B.
220
-
C.
230
-
D.
240
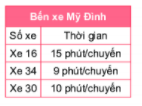
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?
-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
BCNN(10, 15, 30) là:
-
A.
10
-
B.
15
-
C.
30
-
D.
60
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng BCNN(a,b)=300.
-
A.
1
-
B.
2
-
C.
3
-
D.
300
54 và 108 có bội chung nhỏ nhất là
-
A.
54
-
B.
1
-
C.
108
-
D.
216
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác $0$ của nó là $256 .$
-
A.
$16$
-
B.
$18$
-
C.
$24$
-
D.
$32$
Cho tập hợp $X$ là ước của $35$ và lớn hơn $5$. Cho tập $Y$ là bội của $8$ và nhỏ hơn $50$.
Gọi $M$ là giao của $2$ tập hợp $X$ và $Y$, tập hợp $M$ có bao nhiêu phần tử?
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Tìm số tự nhiên \(x\) nhỏ nhất biết \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \,75.\)
-
A.
$1650$
-
B.
$3750$
-
C.
$4950$
-
D.
$3300$
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$
Một số tự nhiên \(a\) khi chia cho \(7\) dư \(4;\) chia cho \(9\) dư \(6.\) Tìm số dư khi chia \(a\) cho \(63.\)
-
A.
$0$
-
B.
$36$
-
C.
$3$
-
D.
$60$
Cho \(a;b\) có \(BCNN\left( {a;b} \right) = 630;\,\)ƯCLN\(\left( {a;b} \right) = 18.\) Có bao nhiêu cặp số \(a;b\) thỏa mãn?
-
A.
$6$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Lời giải và đáp án
Chọn câu trả lời sai.
-
A.
${\rm{5}} \in $ ƯC\(\left( {55;110} \right)\)
-
B.
$24 \in BC\left( {3;4} \right)$
-
C.
$10 \notin $ ƯC\(\left( {55;110} \right)\)
-
D.
$12 = BC\left( {3;4} \right)$
Đáp án : D
Sử dụng kiến thức về ước chung và bội chung
+ Ước chung của hai hay nhiều số là ước của tất cả các số đó.
+ Bội chung của hai hay nhiều số là bội của tất cả các số đó.
+) Ta thấy \(55 \, \vdots \, 5;\,110 \, \vdots \, 5\) nên \(5 \in \) ƯC\(\left( {55;110} \right)\). Do đó A đúng.
+) Vì \(24 \, \vdots \, 3;24 \, \vdots \, 4\) nên \(24 \in BC\left( {3;4} \right)\). Do đó B đúng.
+) Vì \(55\) không chia hết cho \(10\) nên \(10 \notin \) ƯC \(\left( {55;110} \right)\). Do đó C đúng.
+) Vì \(12 \, \vdots \, 3;12 \, \vdots \, 4\) nên \(12 \in BC\left( {3;4} \right)\). Kí hiệu \(12 = BC\left( {3;4} \right)\) là sai. Do đó D sai.
Một trường tổ chức cho học sinh đi tham quan bằng ôtô. Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi. Tính số học sinh đi tam quan biết số lượng học sinh đó trong khoảng từ \(800\) đến \(900\) em.
-
A.
$845$
-
B.
$840$
-
C.
$860$
-
D.
$900$
Đáp án : A
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
+ Sử dụng cách tìm bội chung thông qua bội chung nhỏ nhất.
Gọi số học sinh đi thăm quan là \(x\,\left( {x \in {N^*};\,800 \le x \le 900} \right)\) (học sinh)
Nếu xếp \(35\) hay \(40\) học sinh lên một ô tô thì đều thấy thiếu mất \(5\) ghế ngồi nghĩa là thừa ra 5 học sinh nên ta có
\(\left( {x - 5} \right) \vdots 35;\,\left( {x - 5} \right) \vdots 40\) suy ra \(\left( {x - 5} \right) \in BC\left( {35;40} \right)\).
Ta có \(35 = 5.7;\,40 = {2^3}.5\) nên \(BCNN\left( {35;40} \right) = {2^3}.5.7 = 280.\)
Suy ra \((x-5) \in BC\left( {35;40} \right) = B\left( {280} \right) = \left\{ {280;560;840;1120;...} \right\}\) mà \(800 \le x \le 900\) nên \(x -5= 840\) hay $x=845.$
Vậy số học sinh đi thăm quan là \(845\) học sinh.
Chị Hòa có một số bông sen. Nếu chị bó thành các bó gồm 3 bông, 5 bông hay 7 bông
thì đều vừa hết. Hỏi chị Hòa có bao nhiêu bông sen? Biết rằng chị Hòa có khoảng từ
200 đến 300 bông.
-
A.
210
-
B.
220
-
C.
230
-
D.
240
Đáp án : A
Số bông sen là bội chung của 3, 5, 7 và 200 < x < 300.
- Gọi số bông sen chị Hòa có là: x (bông, \(x \in \mathbb{N}\)).
- Nếu chị bó thành các bỏ bông gồm 3 bông, 5 bông hay 7 bông thì số bông sen chị Hòa có là bội chung của 3, 5 và 7.
- Theo đề bài ta có xe BC(3, 5, 7) và 200 < x < 300
Vì 3, 5, 7 từng đôi một là số nguyên tố cùng nhau.
=> BCNN(3, 5, 7) = 105
=> BC(3, 5, 7) = B(105) = {0; 105, 210, 315;...}
=> x\( \in \) BC(3, 5, 7) ={0, 105, 210, 315,.... }.
Mà \(200 \le x \le 300\) nên x = 210.
Vậy số bông sen chị Hòa có là 210 bông.
Bội chung của hai số a và b luôn là bội của BCNN(a,b).
Lịch xuất bến của một số xe buýt tại bến xe Mỹ Đình (Hà Nội) được ghi ở bảng bên. Giả sử các xe buýt xuất bến cùng lúc vào 10 giờ 35 phút. Hỏi vào sau bao lâu thì cả 3 xe xuất bến cùng một lúc lần nữa (kể từ lần đầu tiên)?

-
A.
90 phút
-
B.
45 phút
-
C.
180 phút
-
D.
30 phút
Đáp án : A
- Tính xem cứ bao nhiêu phút thì các xe xuất bến cùng lúc: BCNN(15, 9, 10)
Thời gian các xe cùng xuất bến cách 10h35p các khoảng thời gian là BC(9, 10, 15)
Ta có: 9 = \({3^2}\), 10 = 2.5, 15 = 3.5.
Thừa số chung và riêng là 2, 3 và 5
Số mũ lớn nhất của 2 là 1
Số mũ lớn nhất của 3 là 2
Số mũ lớn nhất của 5 là 1
=> BCNN(9, 10, 15) = \({2.3^2}.5\) = 90
Vậy cứ 90 phút thì các xe xuất bến cùng một lúc.
Sau 180 phút thì 3 xe cũng xuất bến cùng lúc nhưng không phải là thời gian ngắn nhất.
BCNN(10, 15, 30) là:
-
A.
10
-
B.
15
-
C.
30
-
D.
60
Đáp án : C
Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.
Ta có: 30 là bội của 10 và 15
=> BCNN(10, 15, 30) = 30.
60 cũng là bội chung của 10, 15 và 30 nhưng không phải là bội nhỏ nhất.
Có bao nhiêu số có ba chữ số là bội chung của a và b, biết rằng BCNN(a,b)=300.
-
A.
1
-
B.
2
-
C.
3
-
D.
300
Đáp án : C
- Bội chung của hai số a và b là bội của BCNN(a,b)
- Lấy BCNN(a,b) nhân với các số 1,2,3.
BCNN(a,b) = 300
BC(a,b) là bội của 300.
=> Tất cả các số có 3 chữ số là bội chung của a và b là: 300, 600, 900
Vậy có tất cả 3 số có ba chữ số là bội của a và b.
300 là bội chung nhỏ nhất có ba chữ số của a và b chứ không phải là số các bội.
54 và 108 có bội chung nhỏ nhất là
-
A.
54
-
B.
1
-
C.
108
-
D.
216
Đáp án : C
- Cách tìm BCNN:
+ Phân tích các số ra thừa số nguyên tố.
+ Chọn ra các thừa số nguyên tố chung và riêng.
+ Chọn lũy thừa với số mũ lớn nhất.
+ Lấy tích của các lũy thừa đã chọn.
$54={{2.3}^{3}}$
$108={{2}^{2}}{{.3}^{3}}$
Các thừa số chung của 54 và 108 là 2 và 3.
Số mũ lớn nhất của 2 là 2
Số mũ lớn nhất của 3 là 3.
\(BCNN(54,108)={{2}^{2}}{{.3}^{3}}=108\)
Ta có thể tìm BCNN của 54 và 108 như sau: Trong các số đã cho, nếu số lớn nhất là bội của các số còn lại thì BCNN của các số đã cho chính là số lớn nhất ấy.
Vì $108\vdots 54$ nên \(BCNN(54,108)=108\)
Thực hiện các phép tính sau:\(\dfrac{3}{8} + \dfrac{5}{{24}}\). Với kết quả là phân số tối giản.
-
A.
\(\dfrac{{14}}{{24}}\)
-
B.
\(\dfrac{7}{{12}}\)
-
C.
\(\dfrac{{112}}{{192}}\)
-
D.
\(\dfrac{{12}}{7}\)
Đáp án : B
- Để quy đồng mẫu hai phân số \(\dfrac{a}{b}\) và \(\dfrac{c}{d}\), ta phải tìm mẫu chung của hai phân số đó. Thông thường ta nên chọn mẫu chung là bội chung nhỏ nhất của hai mẫu.
- Để cộng, trừ các phân số khác mẫu ta đi quy đồng mẫu số các phân số rồi thực hiện cộng(trừ) tử số và giữ nguyên mẫu.
Ta có BCNN(8; 24) = 24 nên:
\(\dfrac{3}{8} + \dfrac{5}{{24}} = \dfrac{{3.3}}{{8.3}} + \dfrac{5}{{24}} = \dfrac{9}{{24}} + \dfrac{5}{{24}} = \dfrac{{14}}{{24}} = \dfrac{7}{{12}}\)
\(\dfrac{{14}}{{24}}\) và \(\dfrac{{112}}{{192}}\) đều bằng tổng của các số trên nhưng không là phân số tối giản.
Tìm một số tự nhiên biết tích của ước số lớn nhất với bội số nhỏ nhất khác $0$ của nó là $256 .$
-
A.
$16$
-
B.
$18$
-
C.
$24$
-
D.
$32$
Đáp án : A
Gọi số cần tìm là $a$ $( a \ne 0)$
Ta dùng kiến thức: " Bội nhỏ nhất của một số tự nhiên là chính nó, ước lớn nhất của một số tự nhiên khác $0$ cũng là chính nó" để lập luận và suy ra cách tính $a$.
Gọi số cần tìm là $a$ $( a \ne 0)$
Ước số lớn nhất của $a$ là $a$
Bội số nhỏ nhất khác $0$ của $a$ là $a$
Tích của ước số lớn nhất với bội số nhỏ nhất là:
$a.a = 256 = {16^2}$ nên $a = 16.$
Vậy số cần tìm là \(16.\)
Cho tập hợp $X$ là ước của $35$ và lớn hơn $5$. Cho tập $Y$ là bội của $8$ và nhỏ hơn $50$.
Gọi $M$ là giao của $2$ tập hợp $X$ và $Y$, tập hợp $M$ có bao nhiêu phần tử?
-
A.
$2$
-
B.
$1$
-
C.
$0$
-
D.
$3$
Đáp án : C
- Áp dụng kiến thức ước (bội) của $1$ số, liệt kê tập hợp các ước (bội) số đó.
- So sánh với yêu cầu của đề bài, các ước (bội) lớn hơn (hay nhỏ hơn), để tìm ra tập hợp cuối cùng.
- Dựa vào kiến thức tập hợp để tìm ra tập hợp giao của $2$ tập hợp vừa tìm được.
Ư$(35) = \{ 1,5,7,35\} ;$Ư$(35) > 5 \Rightarrow X = \{ 7,35\} $
$B(8) = \{ 0,8,16,24,32,40,48,56,...\} $
$B(8) < 50 \Rightarrow Y = \{ 0,8,16,24,32,40,48\} $
Vì:
$X = \{ 7,35\} $
$Y = \{ 0,8,16,24,32,40,48\} $
$ \Rightarrow M = X \cap Y = \emptyset $ nên tập M không có phần tử nào.
Tìm số tự nhiên \(x\) nhỏ nhất biết \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \,75.\)
-
A.
$1650$
-
B.
$3750$
-
C.
$4950$
-
D.
$3300$
Đáp án : C
+ Từ đề bài suy ra \(x \in \)BC\(\left( {105;175;385} \right)\) mà \(x\) nhỏ nhất nên \(x = \) BCNN\(\left( {45;75;110} \right)\).
+ Tìm bội chung nhỏ nhất theo các bước
Muốn tìm BCNN của hai hay nhiều số lớn hơn 1, ta thực hiện theo ba bước sau :
Bước 1 : Phân tích mỗi số ra thừa số nguyên tố.
Bước 2 : Chọn ra các thừa số nguyên tố chung và riêng.
Bước 3 : Lập tích các thừa số đã chọn, mỗi thừa số lấy với số mũ lớn nhất của nó. Tích đó là BCNN phải tìm.
Vì \(x \, \vdots \, 45;\,x \, \vdots \, 110\) và \(x \, \vdots \, 75\) nên \(x \, \in BC\left( {45;75;110} \right)\) mà \(x\) nhỏ nhất nên \(x = BCNN\left( {45;75;110} \right)\)
Ta có \(45 = {3^2}.5;\,75 = {3.5^2};\,110 = 2.5.11\)
Nên \(BCNN\left( {45;75;110} \right) = {2.3^2}{.5^2}.11\)\( = 4950.\)
Có bao nhiêu số tự nhiên \(x\) khác \(0\) thỏa mãn $x \in BC(12 ; 15 ; 20) $ và $x$ $ \le $ $100$
-
A.
$4$
-
B.
$3$
-
C.
$2$
-
D.
$1$
Đáp án : D
+ Tìm các bội số nhỏ hơn \(100\) của \(12;15;20.\)
+ Tìm các số chung cho cả ba số \(12;15;20\) trong bội số tìm được.
Ta có \(B\left( {12} \right) = \left\{ {0;12;24;36;48;60;72;84;96;...} \right\}\)
\(B\left( {15} \right) = \left\{ {0;15;30;45;60;75;90;105;...} \right\}\)
\(B\left( {20} \right) = \left\{ {0;20;40;60;80;100;...} \right\}\)
Nên \(BC\left( {12;15;20} \right) = \left\{ {0;60;120;...} \right\}\) mà \(x \le 100\) và \(x \ne 0\) nên \(x = 60.\)
Có một số tự nhiên thỏa mãn đề bài.
Một số tự nhiên \(a\) khi chia cho \(7\) dư \(4;\) chia cho \(9\) dư \(6.\) Tìm số dư khi chia \(a\) cho \(63.\)
-
A.
$0$
-
B.
$36$
-
C.
$3$
-
D.
$60$
Đáp án : D
+ Sử dụng kiến thức về phép chia có dư.
+ Sử dụng kiến thức về bội chung và bội chung nhỏ nhất.
Vì \(a\) chia cho \(7\) dư \(4 \Rightarrow \left( {a + 3} \right) \vdots 7\)
\(a\) chia cho \(9\) dư \(6\) \( \Rightarrow \left( {a + 3} \right) \vdots 9\)
Do đó \(\left( {a + 3} \right) \in BC\left( {7;9} \right)\) mà \(BCNN\left( {7;9} \right) = 63.\)
Do đó \(\left( {a + 3} \right) \vdots 63 \Rightarrow a\) chia cho \(63\) dư \(60.\)
Cho \(a;b\) có \(BCNN\left( {a;b} \right) = 630;\,\)ƯCLN\(\left( {a;b} \right) = 18.\) Có bao nhiêu cặp số \(a;b\) thỏa mãn?
-
A.
$6$
-
B.
$5$
-
C.
$2$
-
D.
$3$
Đáp án : D
+ Vì ƯCLN\(\left( {a;b} \right) = 18\) nên đặt \(a = 18x;\,b = 18y\) với \(x;y \in N;\,\)\(ƯCLN\left( {x;y} \right) = 1;\,y \ne 1.\)
+ Sử dụng ƯCLN\(\left( {a;b} \right).BCNN\left( {a;b} \right) = a.b\) để tìm ra các giá trị \(x;y\) thỏa mãn từ đó suy ra các cặp số \(a;b\) cần tìm.
Vì ƯCLN\(\left( {a;b} \right) = 18\) nên đặt \(a = 18x;\,b = 18y\) với \(x;y \in N;\,\)\(ƯCLN \left( {x;y} \right) = 1;\,y \ne 1.\)
Vì ƯCLN\(\left( {a;b} \right).BCNN\left( {a;b} \right) = a.b\)
Nên \(18.630 = 18x.18y\) \( \Rightarrow x.y = \left( {18.630} \right):\left( {18.18} \right)\) hay \(x.y = 35\) mà \(y \ne 1\)
Do đó ta có:
+) Nếu \(x = 1\) thì \(y = 35\) khi đó \(a = 18.1 = 18;b = 35.18 = 630\)
+) Nếu \(x = 5\) thì \(y = 7\) khi đó \(a = 18.5 = 90;b = 7.18 = 126\)
+) Nếu \(x = 7\) thì \(y = 5\) khi đó \(a = 18.7 = 126;b = 5.18 = 90\)
Vậy có ba cặp số \(a;b\) thỏa mãn.
Tìm hai số tự nhiên $a,b\left( {a < b} \right).$ Biết $a + b = 20,BCNN\left( {a,b} \right) = 15.$
-
A.
$a = 15;b = 25.$
-
B.
$a = 15;b = 5.$
-
C.
$a = 15;b = 20.$
-
D.
$a = 5;b = 15.$
Đáp án : D
Gọi ƯCLN$\left( {a,b} \right) = d$
Tìm $d \in $ ƯC$\left( {15;20} \right)$ sau đó thay $d$ vào công thức $a.b = $ƯCLN$\left( {a,b} \right).BCNN\left( {a,b} \right),$ kết hợp điều kiện $a + b = 20$ để tìm $a$ và $b$.
Gọi ƯCLN$\left( {a,b} \right) = d$ $ \Rightarrow a = d.m,b = d.n;\left( {m,n} \right) = 1$
$ \Rightarrow a + b = d\left( {m + n} \right)$ $ \Rightarrow d \in $ Ư$\left( {a + b} \right)$ hay $d \in $Ư$\left( {20} \right)$
Vì $BCNN\left( {a,b} \right) = 15$ \( \Rightarrow 15 \vdots d\) hay $d \in $Ư$\left( {15} \right)$
$ \Rightarrow d \in $ ƯC$\left( {15;20} \right)$
Mà ƯCLN$\left( {15;20} \right) = 5$ nên $d = 1$ hoặc $d = 5$
+) Nếu $d = 1 \Rightarrow a.b = 1.15 = 15 = 3.5$
Khi đó $a + b = 3 + 5 = 8$ (loại)
Hoặc $a + b = 1 + 15 = 16$ (loại)
+) Nếu $d = 5$ thì $a.b = 5.15 = 75 = 1.75$
Khi đó $a + b = 15 + 5 = 20$ (thỏa mãn)
Hoặc $a + b = 1 + 75 = 76$ (loại)
Vậy hai số cần tìm là $a = 5;b = 15.$
Tìm số tự nhiên n lớn nhất có $3$ chữ số sao cho $n$ chia $8$ dư $7,$ chia $31$ dư $28.$
-
A.
$927$
-
B.
$183$
-
C.
$431$
-
D.
$729$
Đáp án : A
Bước 1: Vì $n$ chia $8$ dư $7,$ chia $31$ dư $28 $ nên:
$\left( {n - 7} \right) \vdots 8$ và $\left( {n - 28} \right) \vdots 31$ $\left( {n > 28} \right)$
Bước 2 : Biến đổi tìm số tự nhiên $m$ sao cho $\left( {n + m} \right) \vdots 8$ và $\left( {n + m} \right) \vdots 31$
Khi đó $\left( {n + m} \right) \vdots BCNN\left( {8;31} \right)$
Bước 3: Tìm các giá trị của $n$
Chọn giá trị của $n$ thỏa mãn $n$ là số lớn nhất có $3$ chữ số
Vì $n$ chia $8$ dư $7$ nên $\left( {n - 7} \right) \vdots 8\,\,\,\,\left( {n > 7} \right)$
$ \Rightarrow n = 8a + 7$ với $a \in \mathbb{N}$$ \Rightarrow \left( {n + 1} \right) \vdots 8$
Vì $n$ chia $31$ dư $28$ nên $\left( {n - 28} \right) \vdots 31\left( {n > 28} \right)$ $ \Rightarrow n = 31b + 28$ $\left( {b \in \mathbb{N}} \right)$
$ \Rightarrow \left( {n + 3} \right) \vdots 31$
Vì $64 \vdots 8$ nên $\left( {n + 1 + 64} \right) \vdots 8$ hay $\left( {n + 65} \right) \vdots 8\left( 1 \right)$
Vì $62 \vdots 31$ $ \Rightarrow \left( {n + 3 + 62} \right) \vdots 31$ hay $\left( {n + 65} \right) \vdots 31$ (2)
Từ (1) và (2) $ \Rightarrow \left( {n + 65} \right) \vdots $$BCNN\left( {8;31} \right)$
$ \Rightarrow \left( {n + 65} \right) \vdots 248$
$ \Rightarrow n = 248k - 65$ $\left( {k \in {\mathbb{N}^ * }} \right)$
Với $k = 1$ $ \Rightarrow n = 248.1 - 65 = 183$
Với $k = 2 \Rightarrow n = 248.2 - 65 = 431$
Với $k = 3 \Rightarrow n = 248.3 - 65 = 679$
Với $k = 4 \Rightarrow n = 248.4 - 65 = 927$
Với $k = 5 \Rightarrow n = 248.5 - 65 = 1175$ (loại)
Vì $n$ là số lớn nhất có $3$ chữ số nên $n = 927.$
Luyện tập và củng cố kiến thức Bài tập cuối chương I Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 13: Bội chung và bội chung nhỏ nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về ước chung và ước chung lớn nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 12: Ước chung và ước chung lớn nhất Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phân tích một số ra thừa số nguyên tố Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 11: Phân tích một số ra thừa số nguyên tố Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về số nguyên tố, hợp số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 10: Số nguyên tố. Hợp số Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về dấu hiệu chia hết cho 3, cho 9 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 9: Dấu hiệu chia hết cho 3, cho 9 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về dấu hiệu chia hết cho 2, cho 5 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 8: Dấu hiệu chia hết cho 2, cho 5 Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về quan hệ chia hết, tính chất chia hết Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Quan hệ chia hết. Tính chất chia hết (tiếp) Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 7: Quan hệ chia hết. Tính chất chia hết Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 6: Thứ tự thực hiện các phép tính Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về phép tính lũy thừa Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 5: Phép tính lũy thừa Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng bài tập về phép nhân, phép chia các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 4: Phép nhân, phép chia các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng bài tập về phép cộng, phép trừ các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 3: Phép cộng, phép trừ các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tập hợp số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 2: Tập hợp các số tự nhiên Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Các dạng toán về tập hợp Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết
Luyện tập và củng cố kiến thức Bài 1: Tập hợp Toán 6 với đầy đủ các dạng bài tập trắc nghiệm có đáp án và lời giải chi tiết










Danh sách bình luận