-
Giải Toán 12 tập 1 - Cánh diều
-
Giải Toán 12 tập 2 - Cánh diều
Giải mục 5 trang 59, 60 SGK Toán 12 tập 2 - Cánh diều
Cho mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0 với (overrightarrow n = (A;B;C)) là vecto pháp tuyến. Cho điểm ({M_0}(2;3;4)). Gọi (H({x_H};{y_H};{z_H})) là hình chiếu vuông góc của điểm ({M_0}) trên mặt phẳng (P) (Hình 16) a) Tính tọa độ của (overrightarrow {H{M_0}} ) theo ({x_H},{y_H},{z_H}) b) Nêu nhận xét về phương của hai vecto (overrightarrow n = (A;B;C)), (overrightarrow {H{M_0}} ). Từ đó, hãy suy ra rằng (left| {overrightarrow n .overrighta
Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều
Toán - Văn - Anh - Hoá - Sinh - Sử - Địa
HĐ10
Trả lời câu hỏi Hoạt động 10 trang 59 SGK Toán 12 Cánh diều
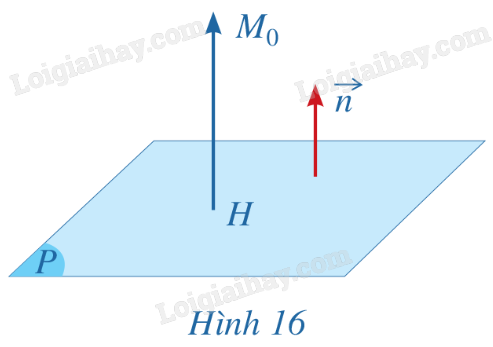
Cho mặt phẳng (P) có phương trình tổng quát là Ax + By + Cz + D = 0 với \(\overrightarrow n = (A;B;C)\) là vecto pháp tuyến. Cho điểm \({M_0}(2;3;4)\). Gọi \(H({x_H};{y_H};{z_H})\) là hình chiếu vuông góc của điểm \({M_0}\) trên mặt phẳng (P).
a) Tính tọa độ của \(\overrightarrow {H{M_0}} \) theo \({x_H}\), \({y_H}\), \({z_H}\).
b) Nêu nhận xét về phương của hai vecto \(\overrightarrow n = (A;B;C)\), \(\overrightarrow {H{M_0}} \). Từ đó, hãy suy ra rằng \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\).
c) Tính các độ dài \(\left| {\overrightarrow n } \right|\), \(\left| {\overrightarrow {H{M_0}} } \right|\) theo A, B, C, D. Từ đó, hãy nêu công thức tính khoảng cách từ điểm \({M_0}(2;3;4)\) đến mặt phẳng (P).
Phương pháp giải:
a) \(A({a_1};{a_2};{a_3})\), \(B({b_1};{b_2};{b_3})\)
\(\Rightarrow \overrightarrow {AB} = ({b_1} - {a_1};{b_2} - {a_2};{b_3} - {a_3})\).
b) Sử dụng các công thức tính tích vô hướng của hai vecto.
c) Sử dụng công thức tính độ dài của vecto. Áp dụng kết quả phần b).
Lời giải chi tiết:
a) \(\overrightarrow {H{M_0}} = (2 - {x_H};3 - {y_H};4 - {z_H})\).
b) Vì H là hình chiếu vuông góc của \({M_0}\) trên mặt phẳng (P) nên 2 vecto \(\overrightarrow n \) và \(\overrightarrow {H{M_0}} \) cùng phương.
Ta có: \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right|.\left| {\cos \left( {\overrightarrow n ;\overrightarrow {H{M_0}} } \right)} \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right|\).
Lại có: \(\overrightarrow n .\overrightarrow {H{M_0}} = A(2 - {x_H}) + B(3 - {y_H}) + C(4 - {z_H}) \)
\(= A.2 + B.3 + C.4 + ( - A{x_H} - B{y_H} - C{z_H})\)
\(= A.2 + B.3 + C.4 + D\).
\( \Rightarrow \left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\).
Vậy \(\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right| = \left| {\overrightarrow n } \right|.\left| {\overrightarrow {H{M_0}} } \right| = \left| {A.2 + B.3 + C.4 + D} \right|\).
c) \(\left| {\overrightarrow n } \right| = \sqrt {{A^2} + {B^2} + {C^2}} \)
\(\left| {\overrightarrow {H{M_0}} } \right| = \frac{{\left| {\overrightarrow n .\overrightarrow {H{M_0}} } \right|}}{{\left| {\overrightarrow n } \right|}} = \frac{{\left| {A.2 + B.3 + C.4 + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Vậy công thức tính khoảng cách từ điểm \({M_0}(2;3;4)\) đến mặt phẳng (P) là \(d({M_0};(P)) = \frac{{\left| {A.2 + B.3 + C.4 + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
LT11
Trả lời câu hỏi Luyện tập 11 trang 60 SGK Toán 12 Cánh diều
Chứng minh rằng khoảng cách từ điểm M(a;b;c) đến các mặt phẳng (Oyz), (Ozx), (Oxy) lần lượt bằng |a|, |b|, |c|.
Phương pháp giải:
Áp dụng công thức tính khoảng cách: \(d\left( {{M_0};(P)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
(Oyz): x = 0; (Ozx): y = 0; (Oxy): z = 0.
\(d\left( {{M_0};(Oyz)} \right) = \frac{{\left| {1.a + 0.b + 0.b + 0} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} }} = \left| a \right|\);
\(d\left( {{M_0};(Ozx)} \right) = \frac{{\left| {0.a + 1.b + 0.b + 0} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} }} = \left| b \right|\);
\(d\left( {{M_0};(Oxy)} \right) = \frac{{\left| {0.a + 0.b + 1.b + 0} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} }} = \left| c \right|\).
LT12
Trả lời câu hỏi Luyện tập 12 trang 60 SGK Toán 12 Cánh diều
Cho mặt phẳng \(({P_1})\): 6x – 8y – 3 = 0 và mặt phẳng \(({P_2})\): 3x – 4y + 2 = 0.
a) Chứng minh rằng \(({P_1})\) // \(({P_2})\).
b) Tính khoảng cách giữa hai mặt phẳng song song \(({P_1})\), \(({P_2})\).
Phương pháp giải:
a) Hai mặt phẳng Ax + By + Cz + D = 0 và A’x + B’y + C’z + D’ = 0 song song nếu:
\(\left\{ \begin{array}{l}A = kA'\\B = kB'\\C = kC'\\D \ne kD'\end{array} \right.\)
b) Lấy một điểm\({M_0} \in ({P_1})\). Ta có \(d\left( {({P_1}),({P_2})} \right) = d\left( {{M_0},({P_2})} \right)\).
Áp dụng công thức tính khoảng cách: \(d\left( {{M_0};(P)} \right) = \frac{{\left| {A{x_0} + B{y_0} + C{z_0} + D} \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).
Lời giải chi tiết:
a) Ta có \(\overrightarrow {{n_1}} = (6; - 8;0)\), \(\overrightarrow {{n_2}} = (3; - 4;0)\) lần lượt là hai vecto pháp tuyến của các mặt phẳng \(({P_1})\), \(({P_2})\).
Do \(\overrightarrow {{n_1}} = 2\overrightarrow {{n_2}} \) và \( - 3 \ne 2\) nên \(({P_1})\) // \(({P_2})\).
b) Chọn điểm \({M_0}\left( {\frac{1}{2};0;0} \right) \in ({P_1})\).
Khoảng cách từ \({M_0}\) đến \(({P_2})\) là:
\(d\left( {{M_0};({P_2})} \right) = \frac{{\left| {3.\frac{1}{2} - 4.0 + 0.0 + 2} \right|}}{{\sqrt {{3^2} + {{( - 4)}^2} + {0^2}} }} = \frac{7}{{10}}\).
Vậy khoảng cách giữa hai mặt phẳng song song \(({P_1})\), \(({P_2})\) bằng \(\frac{7}{{10}}\).
Bình luận
Chia sẻ
- Giải bài tập 1 trang 63 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 2 trang 63 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 3 trang 63 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 4 trang 63 SGK Toán 12 tập 2 - Cánh diều
- Giải bài tập 5 trang 63 SGK Toán 12 tập 2 - Cánh diều
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Cánh diều - Xem ngay
Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí
Các bài khác cùng chuyên mục
