Lý thuyết Nguyên hàm Toán 12 Cánh Diều

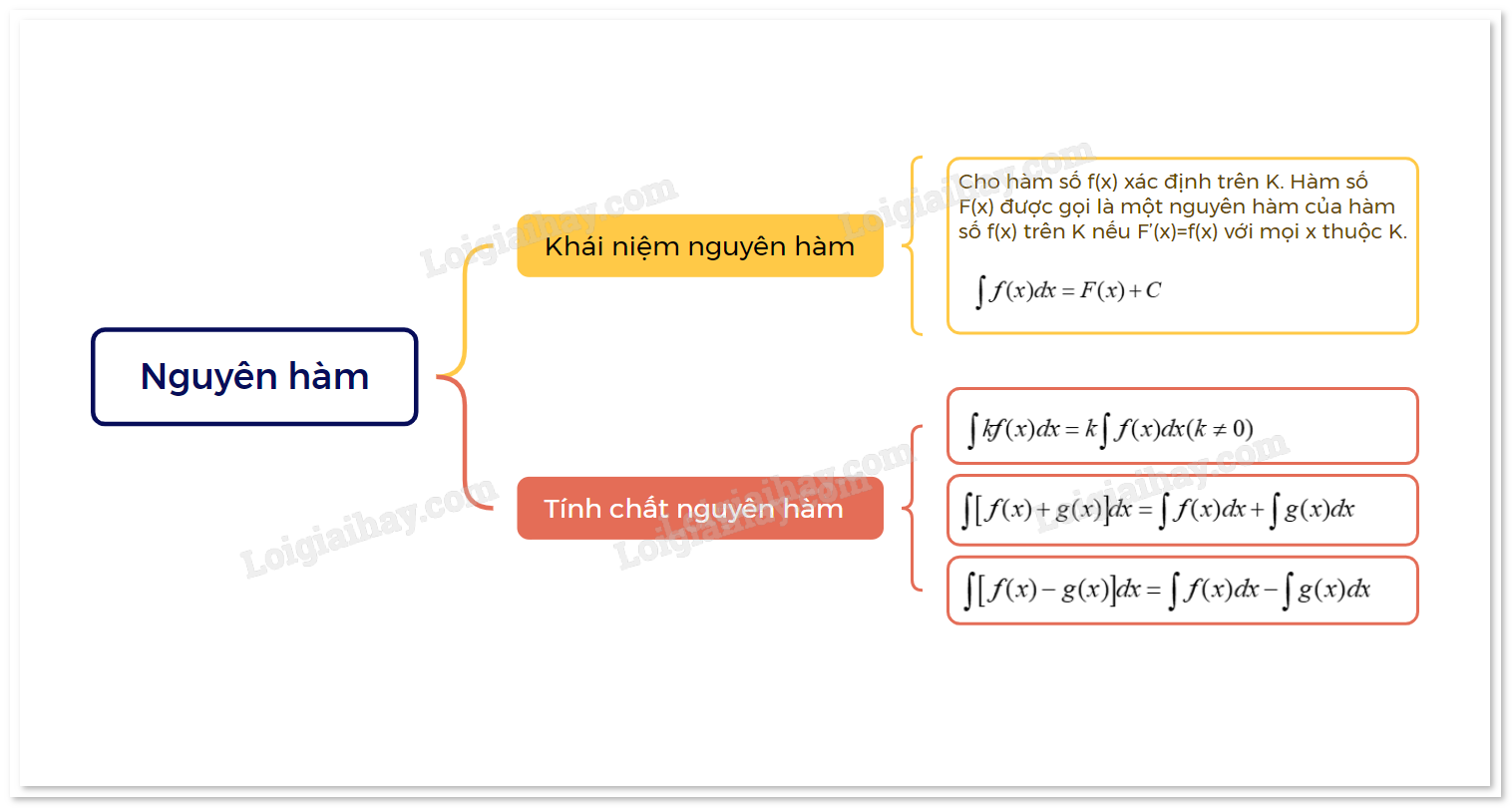
1. Khái niệm nguyên hàm Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K.

1. Khái niệm nguyên hàm

Cho hàm số f(x) xác định trên K. Hàm số F(x) được gọi là một nguyên hàm của hàm số f(x) trên K nếu F’(x)=f(x) với mọi x thuộc K.

Chú ý:

Cho K là một khoảng, đoạn hoặc nửa khoảng của tập số thực R

Giả sử hàm số F(x) là một nguyên hàm của f(x) trên K. Khi đó:

a) Với mỗi hằng số C, hàm số F(x) + C cũng là một nguyên hàm của f(x) trên K

b) Nếu hàm số G(x) là một nguyên hàm của f(x) trên K thì tồn tại một hằng số C sao chp G(x) = F(x) + C với mọi x thuộc K

Họ (hay tập hợp) tất cả các nguyên hàm của hàm số f(x) trên K được kí hiệu là

\(\int {f(x)dx = F(x) + C} \)

2. Tính chất của nguyên hàm

\(\int {kf(x)dx = k\int {f(x)dx(k \ne 0)} } \)
\(\int {\left[ {f(x) + g(x)} \right]} dx = \int {f(x)dx + \int {g(x)dx} } \)
\(\int {\left[ {f(x) - g(x)} \right]} dx = \int {f(x)dx - \int {g(x)dx} } \)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 3,4 SGK Toán 12 tập 2 - Cánh diều
Khái niệm nguyên hàm
Giải mục 2 trang 5,6,7 SGK Toán 12 tập 2 - Cánh diều
Tính chất của nguyên hàm
Giải bài tập 1 trang 7 SGK Toán 12 tập 2 - Cánh diều
Hàm số (F(x) = {x^3} + 5) là nguyên hàm của hàm số: A. (f(x) = 3{x^2}) B. (f(x) = frac{{{x^4}}}{4} + 5x + C) C. (f(x) = frac{{{x^4}}}{4} + 5x) D. (f(x) = 3{x^2} + 5x)
Giải bài tập 2 trang 7 SGK Toán 12 tập 2 - Cánh diều
Tìm nguyên hàm của các hàm số sau: a) \(f(x) = 3{x^2} + x\) b) \(f(x) = 9{x^2} - 2x + 7\) c) \(f(x) = \int {(4x - 3)({x^2}} + 3)dx\)
Giải bài tập 3 trang 7 SGK Toán 12 tập 2 - Cánh diều
Tìm nguyên hàm F(x) của hàm số \(f(x) = 6{x^5} + 2x - 3\), biết F(-1) = -5
Giải bài tập 4 trang 8 SGK Toán 12 tập 2 - Cánh diều
Một vườn ươm cây cảnh bán một cây sau 6 năm trồng và uốn tạo dáng. Tốc độ tăng trưởng trong suốt 6 năm được tính xấp xỉ bởi công thức \(h'(t) = 1,5t + 5\), trong đó h(t) (cm) là chiều cao của cây khi kết thúc t (năm). Cây con khi được trồng cao 12cm a) Tìm công thức chỉ chiều cao của cây sau t năm b) Khi được bán, cây cao bao nhiêu cm?
Giải bài tập 5 trang 8 SGK Toán 12 tập 2 - Cánh diều
Tại một lễ hội dân gian, tốc độ thay đổi lượng khách tham dự được biểu diễn bằng hàm số \(B'(t) = 20{t^3} - 300{t^2} + 1000t\) trong đó t tính bằng giờ (\(0 \le t \le 15\)), B’(t) tính bằng khách/giờ Sau một giờ, 500 người đã có mặt tại lễ hội a) Viết công thức của hàm số B(t) biểu diễn số lượng khách tham dự lễ hội với \(0 \le t \le 15\) b) Sau 3 giờ sẽ có bao nhiêu khách tham dự lễ hội? c) Số lượng khách tham dự lễ hội lớn nhất là bao nhiêu? d) Tại thời điểm nào thì tốc độ thay đổi lượn
Giải bài tập 6 trang 8 SGK Toán 12 tập 2 - Cánh diều
Đối với các dự án xây dựng, chi phí nhân công lao động được tính theo số ngày công. Gọi \(m(t)\) là số lượng công nhân được sử dụng ở ngày thứ t (kể từ khi khởi công dự án). Gọi \(M(t)\) là số ngày công được tính đến hết ngày thứ t (kể từ khi khởi công dự án). Trong kinh tế xây dựng, người ta đã biết rằng \(M'(t) = m(t)\) Một công trình xây dựng dự kiến hoàn thành trong 400 ngày. Số lượng công nhân được sử dụng cho bởi hàm số \(m(t) = 800 - 2t\) trong đó t tính theo ngày (\(0 \le t \le 400\)