Giải toán 10, giải bài tập toán lớp 10 đầy đủ đại số và hình học
Bài 2. Giá trị lượng giác của một cung
Lý thuyết giá trị lượng giác của một cung
1. Định nghĩa
1. Định nghĩa
Trên đường tròn lượng giác cho cung \(\overparen{AM}\) có số đo \(sđ\overparen{AOM}= α\) thì:
+ Tung độ của \(M\) gọi là \(\sin\) của \(α\), kí hiệu \(\sin α\): \(\overline {OQ}= \sinα\)
+ Hoành độ của \(M\) gọi là cosin của \(α\), kí hiệu là \(\cosα\): \(\overline {OP}= \cosα\)
+ Nếu \(cosα \ne 0\), ta gọi là tang của \(α\), kí hiệu \(tanα\) là tỉ số: \({{\sin \alpha } \over {cos\alpha }} = \tan \alpha \)
+ Nếu \(\sinα \ne 0\), ta gọi là cotang của \(α\), kí hiệu là: \({{{\rm{cos}}\alpha } \over {\sin \alpha }} = \cot \alpha \)
Ghi chú: Vì \(sđ\overparen{AM} =sđ\overparen{(OA, OM)}\) nên định nghĩa các giá trị lượng giác của cung lượng giác \(α\) cũng là giá trị lượng giác của góc lượng giác \(α\).
2. Hệ quả
a) \(-1 ≤ sinα ≤ 1, -1 ≤ cosα ≤ 1 ;\)\(∀α \in\mathbb R\)
\(\sin(α + k2π) = \sinα ;∀k \in \mathbb R\)
\(cos(α + k2π) = cosα ,∀k \in\mathbb R\)
b) \(tanα\) xác định với mọi\(α \ne {\pi\over 2} + kπ, k \in\mathbb Z\)
\(cotα\) xác định với mọi \(α \ne kπ, k \in\mathbb Z\)
\(tan(α + kπ) = tanα ,∀k\in\mathbb R\)
\( cot(α + kπ) = cotα ,∀k \in\mathbb R\)
c) Bảng xác định dấu của các giá trị lượng giác
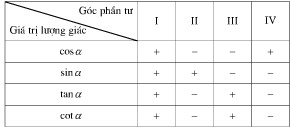
d) Các hệ thức lượng giác cơ bản:
\(si{n^2}\alpha {\rm{ }} + {\rm{ }}co{s^2}\alpha {\rm{ }} = {\rm{ }}1\);
\(tanα.cotα = 1\)
\(1 + {\tan ^2}\alpha = {1 \over {{\rm{co}}{{\rm{s}}^2}\alpha }}\)
\(1 + {\cot ^2}\alpha = {1 \over {{{\sin }^2}\alpha }}\)
3. Giá trị lượng giác của các cung có liên quan đặc biệt
a) Cung đối nhau: \(α\) và \((-α)\)
\(sin(-α) = -sinα \) \( tan(-α) = -tanα\)
\(cos(-α) = cosα\) \(cot(-α) = -cotα\)
b) Cung bù nhau: \(α\) và \(π - α\)
\(sin(π - α) = sinα\) \(tan(π - α) = -tanα\)
\(cos(π - α) = -cosα\) \(cot(π - α) = -cotα\)
c) Cung hơn nhau \(π\): \(α\) và \(π + α\)
\(sin(π + α) = -sinα\) \(tan(π + α) = tanα\)
\(cos(π + α) = -cosα\) \(cot(π + α) = cotα\)
d) Cung phụ nhau: \(α\) và \({\pi \over 2} - \alpha \)
\(sin\left( {{\pi \over 2} - \alpha } \right) = cosα\) \(tan\left( {{\pi \over 2} - \alpha } \right)= cosα\)
\(cos \left( {{\pi \over 2} - \alpha } \right) = sinα \) \(cos=\left( {{\pi \over 2} - \alpha } \right) = tan α\)
Loigiaihay.com
Bình luận
Chia sẻ
- Câu hỏi 1 trang 141 SGK Đại số 10
- Câu hỏi 2 trang 142 SGK Đại số 10
- Câu hỏi 3 trang 143 SGK Đại số 10
- Câu hỏi 4 trang 145 SGK Đại số 10
- Câu hỏi 5 trang 145 SGK Đại số 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
