Lý thuyết Đường thẳng và mặt phẳng song song - SGK Toán 11 Chân trời sáng tạo

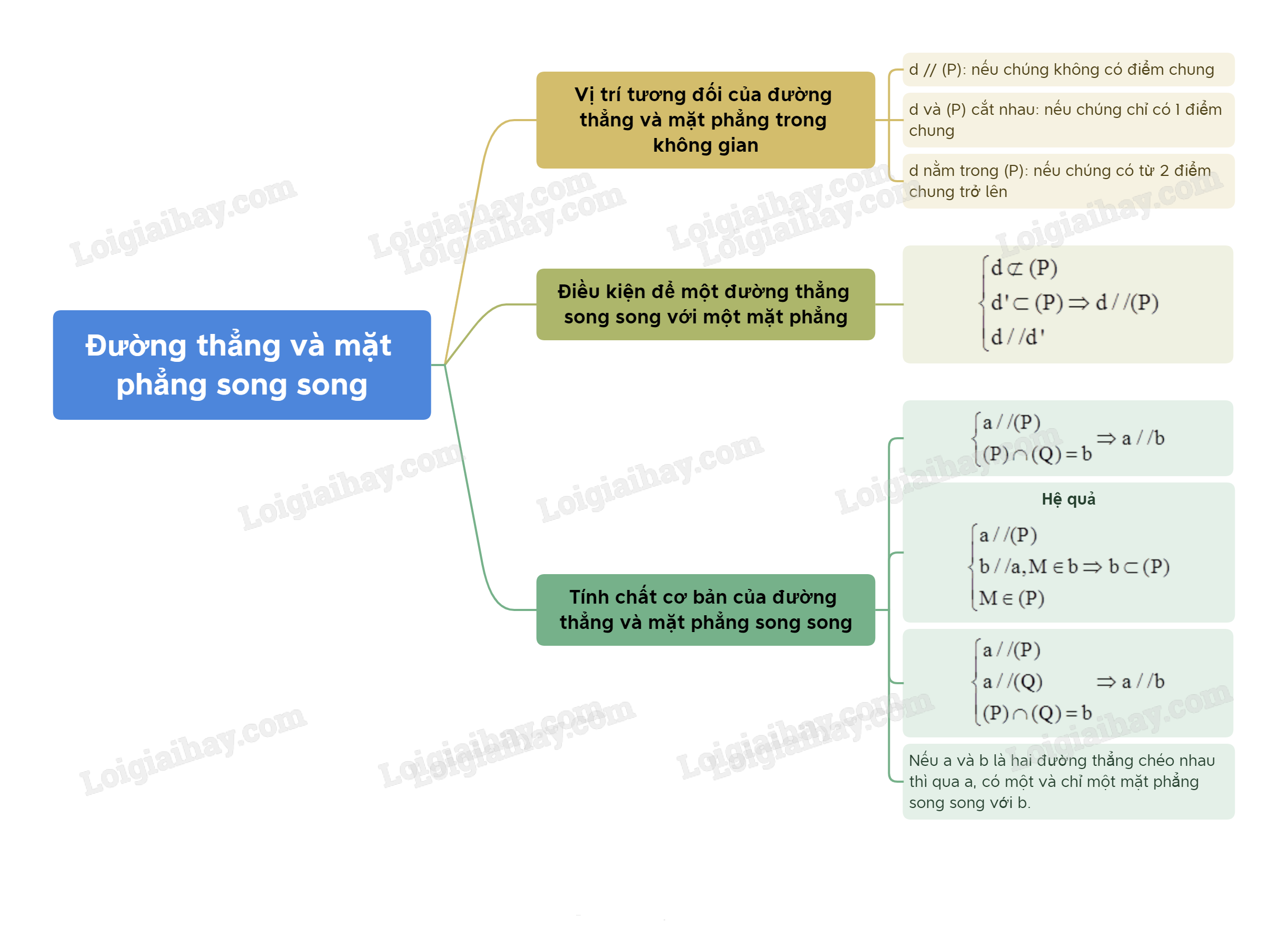
1. Đường thẳng song song với mặt phẳng

Tổng hợp đề thi giữa kì 1 lớp 11 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - Lí - Hóa - Sinh

1. Đường thẳng song song với mặt phẳng

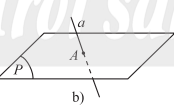
- Nếu a và \(\left( P \right)\) có một điểm chung duy nhất thì ta nói a và \(\left( P \right)\) cắt nhau tại A. Kí hiệu \(a \cap \left( P \right) = A\) hay \(a \cap \left( P \right) = \left\{ A \right\}\).

- Nếu a và \(\left( P \right)\) có từ 2 điểm chung phân biệt trở lên thì ta nói a nằm trong \(\left( P \right)\) hay \(\left( P \right)\) chứa a. Kí hiệu \(a \subset \left( P \right)\) hay \(\left( P \right) \supset a\).

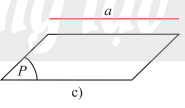
- Nếu a và \(\left( P \right)\) không có điểm chung thì ta nói a song song với \(\left( P \right)\) hay \(\left( P \right)\) song song với a. Kí hiệu là \(a//\left( P \right)\) hay \(\left( P \right)//a\).

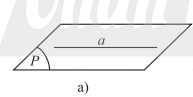
*Đường thẳng a song song với mặt phẳng (P) nếu chúng không có điểm chung.

2. Điều kiện để một đường thẳng song song với một mặt phẳng

Nếu đường thẳng a không nằm trong mặt phẳng (P) và song song với một đường thẳng b nào đó nằm trong (P) thì ta nói \(a//\left( P \right)\).

3. Tính chất cơ bản của đường thẳng và mặt phẳng song song

Cho đường thẳng a song song với mặt phẳng (P). Nếu mặt phẳng (Q) chứa a và cắt (P) theo giao tuyến b thì a // b.

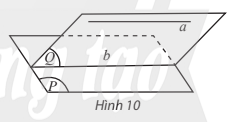
* Hệ quả:

- Cho đường thẳng a song song với mặt phẳng (P). Nếu qua điểm M thuộc (P) ta vẽ đường thẳng b song song với a thì b phải nằm trong (P).

- Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

* Mặt phẳng đi qua một trong hai đường thẳng chéo nhau và song song vơi đường thẳng còn lại

- Nếu a và b là hai đường thẳng chéo nhau thì qua a, có một và chỉ một mặt phẳng song song với b.

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 7 phiếu

Bài tiếp theo

Giải câu hỏi mở đầu trang 107 SGK Toán 11 tập 1 - Chân trời sáng tạo
Đường thẳng a trên mép hiên của tòa nhà có điểm nào chung với mặt (P) của phố đi bộ Nguyễn Huệ không?
Giải mục 1 trang 107, 108 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hai hình bình hành (ABCD) và (ABMN) không đồng phẳng. Tìm số giao điểm của mặt phẳng (left( {ABCD} right)) lần lượt với các đường thẳng (MN,MA) và (AC).
Giải mục 2 trang 108, 109 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho đường thẳng (a) không nằm trong mặt phẳng (left( P right)) và (a) song song với một đường thẳng (b) nằm trong (left( P right)). Đặt (left( Q right) = mpleft( {a,b} right)).
Giải mục 3 trang 109, 110 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho đường thẳng (a) song song với mặt phẳng (left( P right)), mặt phẳng (left( Q right)) chứa (a) và cắt (left( P right)) theo giao tuyến (b) (Hình 10).
Bài 1 trang 111 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hình chóp (S.ABCD), đáy (ABCD) là hình bình hành có (O) là giao điểm hai đường chéo. Cho (M) là trung điểm của (SC).
Bài 2 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hai hình bình hành (ABCD) và (ABEF) không nằm trong cùng một mặt phẳng. Gọi (O) và (O') lần lượt là tâm của (ABCD) và (ABEF).
Bài 3 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hình chóp (S.ABCD) có đáy (ABCD) là hình bình hành và một điểm (M) di động trên cạnh (AD). Một mặt phẳng (left( alpha right)) qua (M), song song với (C{rm{D}}) và (SA), cắt (BC,SC,SD) lần lượt tại (N,P,Q).
Bài 4 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho tứ diện (ABCD) và điểm (M) thuộc cạnh (AB). Gọi (left( alpha right)) là mặt phẳng qua (M), song song với hai đường thẳng (BC) và (AD). Gọi (N,P,Q) lần lượt là giao điểm của mặt phẳng (left( alpha right)) với các cạnh (AC,CD) và (DB).
Bài 5 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang, đáy lớn \(AB\). Gọi \(M\) là trung điểm của \(CD\), \(\left( P \right)\) là mặt phẳng qua \(M\) song song với \(SA\) và \(BC\). Tìm giao tuyến của \(\left( P \right)\) với các mặt của hình chóp \(S.ABCD\).
Bài 6 trang 112 SGK Toán 11 tập 1 - Chân trời sáng tạo
Mô tả vị trí tương đối của các đường thẳng (a,b,c,d,e) với mặt phẳng (left( P right)) là mặt trước của toà nhà (Hình 19).