-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Toán 9 cùng khám phá | Giải toán lớp 9 cùng khám phá
Bài 1. Căn bậc hai của một số thực không âm - Toán 9 Cù..
Lý thuyết Căn bậc hai của một số thực không âm Toán 9 Cùng khám phá
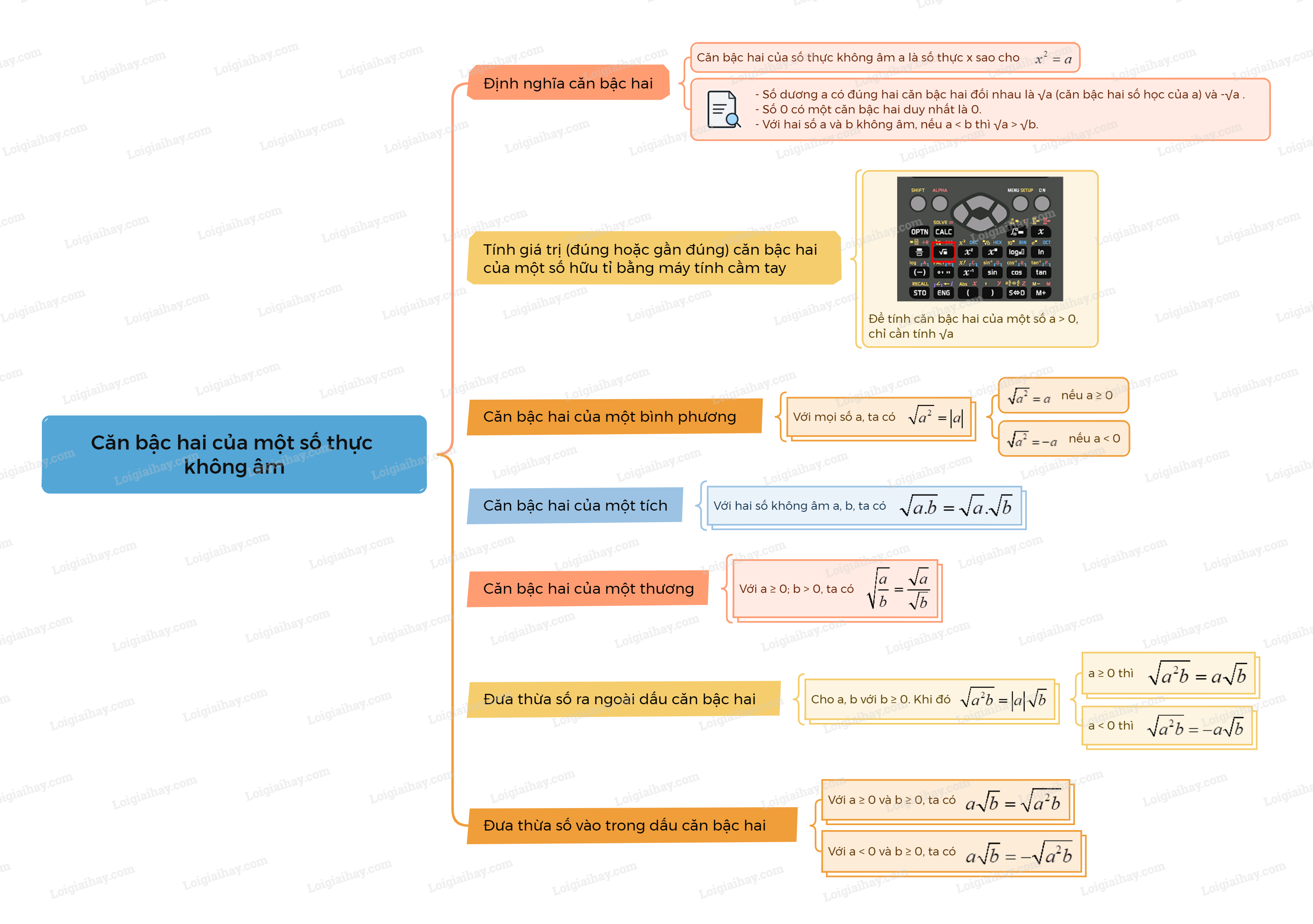
1. Khái niệm về căn bậc hai của số thực không âm Định nghĩa căn bậc hai Căn bậc hai của một số thực a không âm là số x sao cho . Lưu ý:
1. Khái niệm về căn bậc hai của số thực không âm
Định nghĩa căn bậc hai
|
Căn bậc hai của một số thực a không âm là số x sao cho \({x^2} = a\). |
Lưu ý:
- Số dương a có đúng hai căn bậc hai là hai số đối nhau, trong đó số dương là \(\sqrt a \) và số âm là \( - \sqrt a \).
- Số 0 có đúng một căn bậc hai là chính nó, ta viết \(\sqrt 0 = 0\).
- Với hai số a và b không âm, nếu \(a < b\) thì \(\sqrt a < \sqrt b \).
Ví dụ:
+) \(\sqrt {81} = 9\) nên 81 có hai căn bậc hai là 9 và -9.
+) Căn bậc hai số học của 121 là \(\sqrt {121} = 11\).
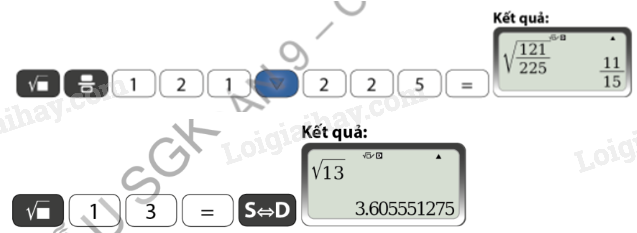
2. Tính giá trị (đúng hoặc gần đúng) căn bậc hai của một số hữu tỉ bằng máy tính cầm tay
|
Để tính các căn bậc hai của một số \(a > 0\), chỉ cần tính \(\sqrt a \). Có thể dễ dàng làm điều này bằng cách sử dụng MTCT.
Sử dụng nút này để bấm căn bậc hai. |
Ví dụ:
3. Căn bậc hai của một bình phương
|
Với mọi số thực a, ta có: \(\sqrt {{a^2}} = \left| a \right|\). Như vậy: \(\sqrt {{a^2}} = a\) nếu \(a \ge 0\); \(\sqrt {{a^2}} = - a\) nếu \(a < 0\). |
Ví dụ: \(\sqrt {{{\left( {1 + \sqrt 2 } \right)}^2}} = \left| {1 + \sqrt 2 } \right| = 1 + \sqrt 2 \); \(\sqrt {{{\left( { - 3} \right)}^2}} = \left| { - 3} \right| = 3\).
4. Căn bậc hai của một tích
|
Nếu a và b là hai số không âm thì \(\sqrt {a.b} = \sqrt a .\sqrt b \). |
Ví dụ:
\(\sqrt {81.49} = \sqrt {81} .\sqrt {49} = 9.7 = 63\);
\(\sqrt {1,3} .\sqrt {10} .\sqrt {13} = \sqrt {1,3.10.13} = \sqrt {13.13} = \sqrt {{{13}^2}} = 13\).
Lưu ý: Tính chất trên có thể mở rộng cho tích của nhiều số không âm. Chẳng hạn với a, b, c là ba số không âm, ta có \(\sqrt {abc} = \sqrt a .\sqrt b .\sqrt c \).
5. Căn bậc hai của một thương
|
Nếu a là số không âm và b là số dương thì \(\sqrt {\frac{a}{b}} = \frac{{\sqrt a }}{{\sqrt b }}\). |
Ví dụ:
\(\sqrt {\frac{4}{{25}}} = \frac{{\sqrt 4 }}{{\sqrt {25} }} = \frac{2}{5}\);
\(\frac{{\sqrt {216} }}{{\sqrt 6 }} = \sqrt {\frac{{216}}{6}} = \sqrt {36} = 6\).
6. Đưa thừa số ra ngoài hoặc vào trong dấu căn bậc hai
Đưa thừa số ra ngoài dấu căn
|
Nếu \(a \ge 0\) và \(b \ge 0\) thì \(\sqrt {{a^2}b} = a\sqrt b \). Nếu \(a < 0\) và \(b \ge 0\) thì \(\sqrt {{a^2}b} = - a\sqrt b \). |
Ví dụ:
\(\sqrt {{7^2}.2} = 7\sqrt 2 \);
\(\sqrt {{{\left( { - 11} \right)}^2}.3} = \left| { - 11} \right|.\sqrt 3 = 11\sqrt 3 \).
Đưa thừa số vào trong dấu căn
|
Nếu \(a \ge 0\) và \(b \ge 0\) thì \(a\sqrt b = \sqrt {{a^2}b} \). Nếu \(a < 0\) và \(b \ge 0\) thì \(a\sqrt b = - \sqrt {{a^2}b} \). |
Ví dụ:
\(2\sqrt {\frac{1}{2}} = \sqrt {{2^2}.\frac{1}{2}} = \sqrt 2 \);
\(4\sqrt {\frac{7}{4}} - \sqrt {28} = \sqrt {{4^2}.\frac{7}{4}} - \sqrt {28} = \sqrt {4.7} - \sqrt {28} = \sqrt {28} - \sqrt {28} = 0\).
Bình luận
Chia sẻ
- Giải mục 1 trang 51, 52 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 2 trang 52 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 3 trang 53 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 4 trang 53, 54 SGK Toán 9 tập 1 - Cùng khám phá
- Giải mục 5 trang 55 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
