Giải mục 3 trang 73, 74 SGK Toán 9 tập 2 - Cùng khám phá

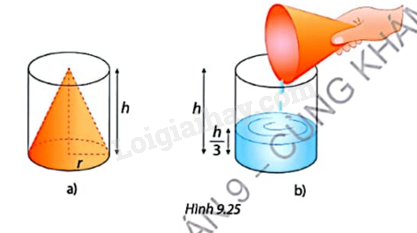
Bạn Thiện có một phễu đong dạng hình nón (Hình 9.25a) và một thùng không chứa dạng hình trụ (Hình 9.25b) với cùng bán kính đáy r và chiều cao h. Thiện dùng phễu đong đày nước rồi đổ vào thùng chứa thì thấy rằng mực nước bằng \(\frac{1}{3}\) chiều cao của thùng. a) Tính thể tích V của phần nước trong thùng chứa theo r và h. b) Hãy dự đoán thể tích của phễu đong.

Lựa chọn câu để xem lời giải nhanh hơn

HĐ3

Trả lời câu hỏi Hoạt động 3 trang 73 SGK Toán 9 Cùng khám phá

Bạn Thiện có một phễu đong dạng hình nón (Hình 9.25a) và một thùng không chứa dạng hình trụ (Hình 9.25b) với cùng bán kính đáy r và chiều cao h.

Thiện dùng phễu đong đày nước rồi đổ vào thùng chứa thì thấy rằng mực nước bằng \(\frac{1}{3}\) chiều cao của thùng.

a) Tính thể tích V của phần nước trong thùng chứa theo r và h.

b) Hãy dự đoán thể tích của phễu đong.

Phương pháp giải:

Dựa theo thể tích hình trụ: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ).

Lời giải chi tiết:

a) Thể tích của phần nước trong thùng là:

\(V = \pi {r^2}\frac{h}{3}\).

b) Thể tích của phễu đong bằng \(\frac{1}{3}\) thể tích hình trụ.

LT3

Trả lời câu hỏi Luyện tập 3 trang 73 SGK Toán 9 Cùng khám phá

Một hình nón có đường sinh bằng 10 cm và chiều cao bằng 8 cm. Tính thể tích của hình nón.

Phương pháp giải:

Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).

Lời giải chi tiết:

Bán kính đáy của hình nón là:

\(\sqrt {{{10}^2} - {8^2}} = 6\) cm

Thể tích hình nón là:

\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.8 = 96\pi \) (cm³).

VD3

Trả lời câu hỏi Vận dụng 3 trang 74 SGK Toán 9 Cùng khám phá

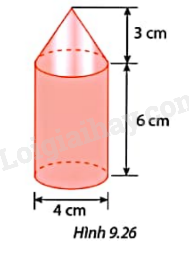
Tính thể tích của mô hình tên lửa trong Hình 9.26.

Phương pháp giải:

Thể tích hình trụ: \(V = \pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình trụ).

Thể tích hình nón: \(V = \frac{1}{3}\pi {r^2}h\) (với r là bán kính đáy và h là chiều cao của hình nón).

Lời giải chi tiết:

Thể tích hình trụ là:

\(V = \pi {r^2}h = \pi {.2^2}.6 = 24\pi \) (cm³).

Thể tích hình nón là:

\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.2^2}.3 = 4\pi \)(cm³).

Thể tích của mô hình tên lửa là:

\(24\pi + 4\pi = 28\pi \)(cm³).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 4 trang 74, 75 SGK Toán 9 tập 2 - Cùng khám phá
Bước 1: Cắt miếng bìa như Hình 9.27a rồi uốn miếng bìa lại và dán hai mép OA, OB sao cho chúng chồng khít lên nhau tạo thành mặt xung quanh của hình nón đỉnh O (không có đáy) như Hình 9.27b. Bước 2: Tính bán kính đáy r của hình nón tạo thành và cắt miếng bìa hình tròn bán kính r. Dùng băng dính dán miếng bìa này với mặt xung quanh của hình nón ở Bước 1 để tạo lập thành một hình nón.
Giải bài tập 9.6 trang 75 SGK Toán 9 tập 2 - Cùng khám phá
Kể tên đỉnh, chiều cao, đường sinh, bán kính đáy và tính diện tích xung quanh, thể tích của hình nón ở Hình 9.29.
Giải bài tập 9.7 trang 75 SGK Toán 9 tập 2 - Cùng khám phá
Tìm các số và đơn vị thích hợp để hoàn thành Bảng 9.2.
Giải bài tập 9.8 trang 76 SGK Toán 9 tập 2 - Cùng khám phá
Tính diện tích bìa cần dùng (theo centimet vuông) để làm một chiếc mũ sinh nhật có dạng hình nón như Hình 9.30 với đường kính đáy 22 cm và chiều cao 18 cm (bỏ qua các mép nối và phần thừa, làm tròn kết quả đến centimet vuông).
Giải bài tập 9.9 trang 76 SGK Toán 9 tập 2 - Cùng khám phá
Thả 10 chiếc đinh có kích thước như Hình 9.31 vào một cốc nước thuỷ tinh. Đinh chìm hẳn xuống và nước trong cốc không bị trần ra ngoài. Hỏi thể tích nước trong cốc tăng thêm bao nhiêu mililit (làm tròn kết quả đến hàng phần mười)?
Giải mục 2 trang 71, 72 SGK Toán 9 tập 2 - Cùng khám phá
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b). a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b. b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Giải mục 1 trang 69, 70, 71 SGK Toán 9 tập 2 - Cùng khám phá
Trong Hình 9.17, những vật thể nào có hình dáng giống nhau?
Lý thuyết Hình nón Toán 9 Cùng khám phá
1. Hình nón Chú ý: Cho hình nón có bán kính đáy r, chiều cao h và đường sinh l.