-
Toán 9 tập 1 - Cùng khám phá
-
Toán 9 tập 2 - Cùng khám phá
Giải mục 2 trang 71, 72 SGK Toán 9 tập 2 - Cùng khám phá
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b). a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b. b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
HĐ2
Trả lời câu hỏi Hoạt động 2 trang 71 SGK Toán 9 Cùng khám phá
Cắt mặt xung quanh của một hình nón có đường sinh dài 6 cm, bán kính đáy 2 cm (Hình 9.22a) dọc theo đường sinh SA của nó rồi trải phẳng ra, ta được hình khai triển của hình nón đó (Hình 9.22b).
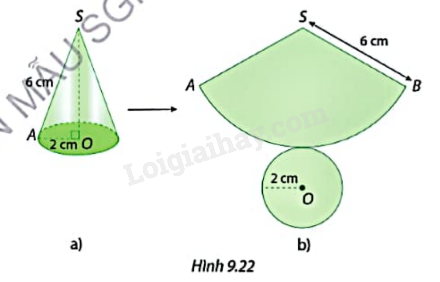
a) Tính chu vi đáy của hình nón, từ đó cho biết độ dài cung ứng với hình quạt tròn ở Hình 9.22b.
b) Tính diện tích của hình quạt tròn khai triển trong Hình 9.22b.
Phương pháp giải:
Chu vi đường tròn: C = \(\pi {r^2}\)(r là bán kính đường tròn).
Lời giải chi tiết:
a) Chu vi đáy hình nón là:
\(\pi {r^2} = 4\pi \)(cm).
Suy ra độ dài cung ứng với hình quạt tròn là: \(r.n\) (n: số đo góc ở tâm chắn cung đó).
b) Diện tích hình quạt tròn khai triển là:
S = \(\frac{{\pi .{r^2}.n}}{{360}}\).
LT2
Trả lời câu hỏi Luyện tập 2 trang 72 SGK Toán 9 Cùng khám phá
Tính chiều cao của một hình nó có đường sinh dài 20 cm và diện tích xung quanh bằng 240\(\pi \)cm2.
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có:\({S_{xq}} = \pi rn\)
suy ra r = \(\frac{{{S_{xq}}}}{{\pi .n}} = \frac{{240\pi }}{{\pi .20}} = 12\)cm.
Từ đó, ta có chiều cao của hình nón là:
\(\sqrt {{{20}^2} - {{12}^2}} = 16\) cm (Theo định lý Pythagore).
VD2
Trả lời câu hỏi Vận dụng 2 trang 72 SGK Toán 9 Cùng khám phá
Nón lá phổ biến ở cả ba miền của nước ta nhưng nón lá Huế từ lâu đã trở thành nguồn cảm hứng cho thi ca. Nón Huế thường có màu trắng xanh, thanh tao, mỏng, nhẹ, mềm mại. Nón lá Huế có khung gồm 16 vòng cách đều nhau (khuôn nón còn được gọi là khung chằm) và được lợp bằng nhiều lớp lá của cây lá nón trồng ở huyện A Lưới và huyện Nam Đông, thuộc tỉnh Thừa Thiên Huế. Tính diện tích bề mặt ngoài (theo centimet vuông) của một chiếc nón lá có đường kính đáy 41 cm và chiều cao 18 cm (làm tròn kết quả đến hàng phần mười).
Phương pháp giải:
Diện tích xung quanh của hình nón: \({S_{xq}} = \pi rn\) (với r là bán kính đáy và n là đường sinh của hình nón).
Lời giải chi tiết:
Ta có đường sinh của chiếc nón lá là:
\(\sqrt {{{\left( {\frac{{41}}{2}} \right)}^2} + {{18}^2}} \approx 27,3\) cm (theo định lí pythagore)
Vậy diện tích bề mặt ngoài của chiếc nón lá là:
\({S_{xq}} = \pi rn = \pi .\frac{{41}}{2}.27,3 \approx 1758,2\)cm2
Bình luận
Chia sẻ
- Giải mục 3 trang 73, 74 SGK Toán 9 tập 2 - Cùng khám phá
- Giải mục 4 trang 74, 75 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 9.6 trang 75 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 9.7 trang 75 SGK Toán 9 tập 2 - Cùng khám phá
- Giải bài tập 9.8 trang 76 SGK Toán 9 tập 2 - Cùng khám phá
>> Xem thêm
Tham Gia Group 2K10 Ôn Thi Vào Lớp 10 Miễn Phí
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
