Bài 2. Phương trình đường thẳng - Toán 12 Cánh diều

Giải mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh diều

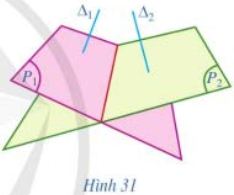
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).

Lựa chọn câu để xem lời giải nhanh hơn

HĐ8

Trả lời câu hỏi Hoạt động 8 trang 74 SGK Toán 12 Cánh diều

Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).

a) Nêu cách xác định góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\).

b) Góc đó có phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\) như trên không?

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai đường thẳng để tính: Góc giữa hai đường thẳng m và n trong không gian là góc giữa hai đường thẳng a và b cùng đi qua một điểm và tương ứng song song với m và n.

Lời giải chi tiết:

a) Vẽ hai đường thẳng \(\Delta _1',\Delta _2'\) cùng đi qua điểm I và lần lượt song song (hoặc trùng) với \({\Delta _1},{\Delta _2}\). Khi đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\).

b) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) và \(\Delta _1'\) song song (hoặc trùng) với \({\Delta _1}\) nên \(\Delta _1' \bot \left( {{P_1}} \right)\).

Tương tự ta có: \(\Delta _2' \bot \left( {{P_2}} \right)\).

Khi đó, góc giữa hai đường thẳng \(\Delta _1',\Delta _2'\) luôn là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\) nên góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) không phụ thuộc vào việc chọn hai đường thẳng \({\Delta _1},{\Delta _2}\).

LT8

Trả lời câu hỏi Luyện tập 8 trang 74 SGK Toán 12 Cánh diều

Trong Ví dụ 10, tính góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’).

Phương pháp giải:

Sử dụng kiến thức về góc giữa hai mặt phẳng để tính góc giữa hai mặt phẳng: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó.

Lời giải chi tiết:

Vì ADD’A’ là hình vuông nên \(AD' \bot A'D\). Vì \(CD \bot \left( {ADD'A'} \right)\) nên \(CD \bot AD'\). Do đó, \(AD' \bot \left( {CDA'B'} \right)\).

Mặt khác, \(C'D' \bot \left( {BCC'B'} \right)\), suy ra góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) là góc giữa hai đường thẳng AD’ và C’D’, đó là góc AD’C’.

Vì \(C'D' \bot \left( {ADD'A'} \right)\) nên \(C'D' \bot AD'\), suy ra . Do đó, góc giữa hai mặt phẳng (BCC’B’) và (CDA’B’) bằng 90 độ.

HĐ9

Trả lời câu hỏi Hoạt động 9 trang 75 SGK Toán 12 Cánh diều

Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Gọi \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right),\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\) lần lượt là hai vectơ pháp tuyến của \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\); \({\Delta _1},{\Delta _2}\) lần lượt là giá của hai vectơ \(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) (Hình 33). So sánh:

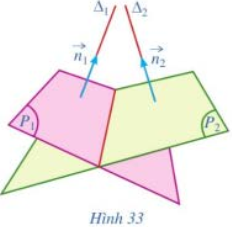
a) \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right)\) và \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\);

b) \(\cos \left( {{\Delta _1},{\Delta _2}} \right)\) và \(\left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).

Phương pháp giải:

Sử dụng kiến thức vectơ pháp tuyến của mặt phẳng để chứng minh: Nếu vectơ \(\overrightarrow n \) khác \(\overrightarrow 0 \) và có giá vuông góc với mặt phẳng (P) thì \(\overrightarrow n \) được gọi là vectơ pháp tuyến của mặt phẳng (P).

Sử dụng kiến thức về vectơ chỉ phương của đường thẳng để chứng minh: Cho đường thẳng \(\Delta \) và vectơ \(\overrightarrow u \) khác \(\overrightarrow 0 \). Vectơ \(\overrightarrow u \) được gọi là vectơ chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).

Lời giải chi tiết:

a) Vì \({\Delta _1} \bot \left( {{P_1}} \right)\) nên đường thẳng \({\Delta _1}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_1}} \) của mặt phẳng \(\left( {{P_1}} \right)\) làm một vectơ chỉ phương.

Vì \({\Delta _2} \bot \left( {{P_2}} \right)\) nên đường thẳng \({\Delta _2}\) nhận một vectơ pháp tuyến \(\overrightarrow {{n_2}} \) của mặt phẳng \(\left( {{P_2}} \right)\) làm một vectơ chỉ phương.

Do đó, góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) là góc giữa hai vectơ pháp tuyến \(\overrightarrow {{n_1}} \) và \(\overrightarrow {{n_2}} \).

Vậy \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \cos \left( {{\Delta _1},{\Delta _2}} \right)\).

b) Ta có:\(\cos \left( {{\Delta _1},{\Delta _2}} \right) = \cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right|\).

LT9

Trả lời câu hỏi Luyện tập 9 trang 75 SGK Toán 12 Cánh diều

Cho mặt phẳng (P) có vectơ pháp tuyến \(\overrightarrow n = \left( {A;B;C} \right)\). Tính côsin của góc giữa mặt phẳng (P) và các mặt phẳng tọa độ.

Phương pháp giải:

Sử dụng kiến thức về côsin góc giữa hai mặt phẳng để tính: Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(\left( {{P_1}} \right)\), \(\left( {{P_2}} \right)\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {{A_1};{B_1};{C_1}} \right)\), \(\overrightarrow {{n_2}} = \left( {{A_2};{B_2};{C_2}} \right)\). Khi đó, ta có: \(\cos \left( {\left( {{P_1}} \right),\left( {{P_2}} \right)} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\).

Lời giải chi tiết:

Mặt phẳng (Oxy) có một vectơ pháp tuyến là \(\overrightarrow k = \left( {0;0;1} \right)\); mặt phẳng (Oxz) có một vectơ pháp tuyến là \(\overrightarrow j = \left( {0;1;0} \right)\); mặt phẳng (Oyz) có một vectơ pháp tuyến là \(\overrightarrow i = \left( {1;0;0} \right)\)

Do đó, \(\cos \left( {\left( {Oxy} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 0.B + 1.C} \right|}}{{\sqrt {{0^2} + {0^2} + {1^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| C \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\cos \left( {\left( {Oxz} \right),\left( P \right)} \right) = \frac{{\left| {0.A + 1.B + 0.C} \right|}}{{\sqrt {{0^2} + {1^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| B \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\);

\(\cos \left( {\left( {Oyz} \right),\left( P \right)} \right) = \frac{{\left| {1.A + 0.B + 0.C} \right|}}{{\sqrt {{1^2} + {0^2} + {0^2}} \sqrt {{A^2} + {B^2} + {C^2}} }} = \frac{{\left| A \right|}}{{\sqrt {{A^2} + {B^2} + {C^2}} }}\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài tập 1 trang 78 SGK Toán 12 tập 2 - Cánh diều
Đường thẳng đi qua điểm A(3; 2; 5) nhận \(\overrightarrow u = \left( { - 2;8; - 7} \right)\) làm vectơ chỉ phương có phương trình tham số là:
Giải bài tập 2 trang 78 SGK Toán 12 tập 2 - Cánh diều
Đường thẳng đi qua điểm \(B\left( { - 1;3;6} \right)\) nhận \(\overrightarrow u = \left( {2; - 3;8} \right)\) làm vectơ chỉ phương có phương trình chính tắc là:
Giải bài tập 3 trang 78 SGK Toán 12 tập 2 - Cánh diều
Mặt phẳng \(\left( P \right):x - 2 = 0\) vuông góc với mặt phẳng nào sau đây? A. \(\left( {{P_1}} \right):x + 2 = 0\). B. \(\left( {{P_2}} \right):x + y - 2 = 0\). C. \(\left( {{P_3}} \right):z - 2 = 0\). D. \(\left( {{P_4}} \right):x + z - 2 = 0\).
Giải bài tập 4 trang 78 SGK Toán 12 tập 2 - Cánh diều
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - t\\y = 3 + 2t\\z = - 1 + 3t\end{array} \right.\)(t là tham số). a) Chỉ ra tọa độ hai điểm thuộc đường thẳng \(\Delta \). b) Điểm nào trong các điểm \(C\left( {6; - 7; - 16} \right),D\left( { - 3;11; - 11} \right)\) thuộc đường thẳng \(\Delta \)?
Giải bài tập 5 trang 78, 79 SGK Toán 12 tập 2 - Cánh diều
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(\Delta \) trong mỗi trường hợp sau: a) \(\Delta \) đi qua điểm \(A\left( { - 1;3;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 2;3;4} \right)\). b) \(\Delta \) đi qua hai điểm \(M\left( {2; - 1;3} \right)\) và \(N\left( {3;0;4} \right)\).
Giải bài tập 6 trang 79 SGK Toán 12 tập 2 - Cánh diều
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau: a) \({\Delta _1}:\frac{{x - 1}}{2} = \frac{{y - 2}}{1} = \frac{{z - 3}}{{ - 1}}\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 11 - 6t\\y = - 6 - 3t\\z = 10 + 3t\end{array} \right.\) (t là tham số); b) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 + 4t\\z = 3 + 5t\end{array} \right.\) (t là tham số) và \({\Delta _2}:\frac{{x + 3}}{1} = \frac{{y + 6}}{2} = \frac{{z - 15}}{{ - 3}}\)
Giải bài tập 7 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ): a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + {t_1}\\y = 4 + \sqrt 3 {t_1}\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_2}\\y = 4 + {t_2}\\z = 5\end{array} \right.\) (\({t_1},{t_2}\) là tham số); b) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 + t\\z = 4 - t\end{array} \right.\) (t là tham số) và \({\Del
Giải bài tập 8 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ): a) \(\Delta :\left\{ \begin{array}{l}x = 1 + \sqrt 3 t\\y = 2\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):\sqrt 3 x + z - 2 = 0\); b) \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):x + y + z - 4 = 0\).
Giải bài tập 9 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right):x + y + 2z - 1 = 0\) và \(\left( {{P_2}} \right):2x - y + z - 2 = 0\).
Giải bài tập 10 trang 80 SGK Toán 12 tập 2 - Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S. ABCD có các đỉnh lần lượt là (Sleft( {0;0;frac{{asqrt 3 }}{2}} right),Aleft( {frac{a}{2};0;0} right),Bleft( { - frac{a}{2};0;0} right),Cleft( { - frac{a}{2};a;0} right),Dleft( {frac{a}{2};a;0} right)) với (a > 0) (Hình 36).
Giải bài tập 11 trang 80 SGK Toán 12 tập 2 - Cánh diều
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí \(A\left( {3,5; - 2;0,4} \right)\) và sẽ hạ cánh ở vị trí \[B\left( {3,5;5,5;0} \right)\] trên đường băng EG (Hình 37).
Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh diều
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) . a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
Giải mục 1 trang 65, 66, 67, 68, 69 SGK Toán 12 tập 2 - Cánh diều
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ (overrightarrow {A'C'} ) và đường thẳng AC có vị trí tương đối như thế nào?
Lý thuyết Phương trình đường thẳng Toán 12 Cánh Diều
1. Phương trình đường thẳng a) Vecto chỉ phương của đường thẳng