Lý thuyết Phương trình đường thẳng Toán 12 Cánh Diều

1. Phương trình đường thẳng a) Vecto chỉ phương của đường thẳng

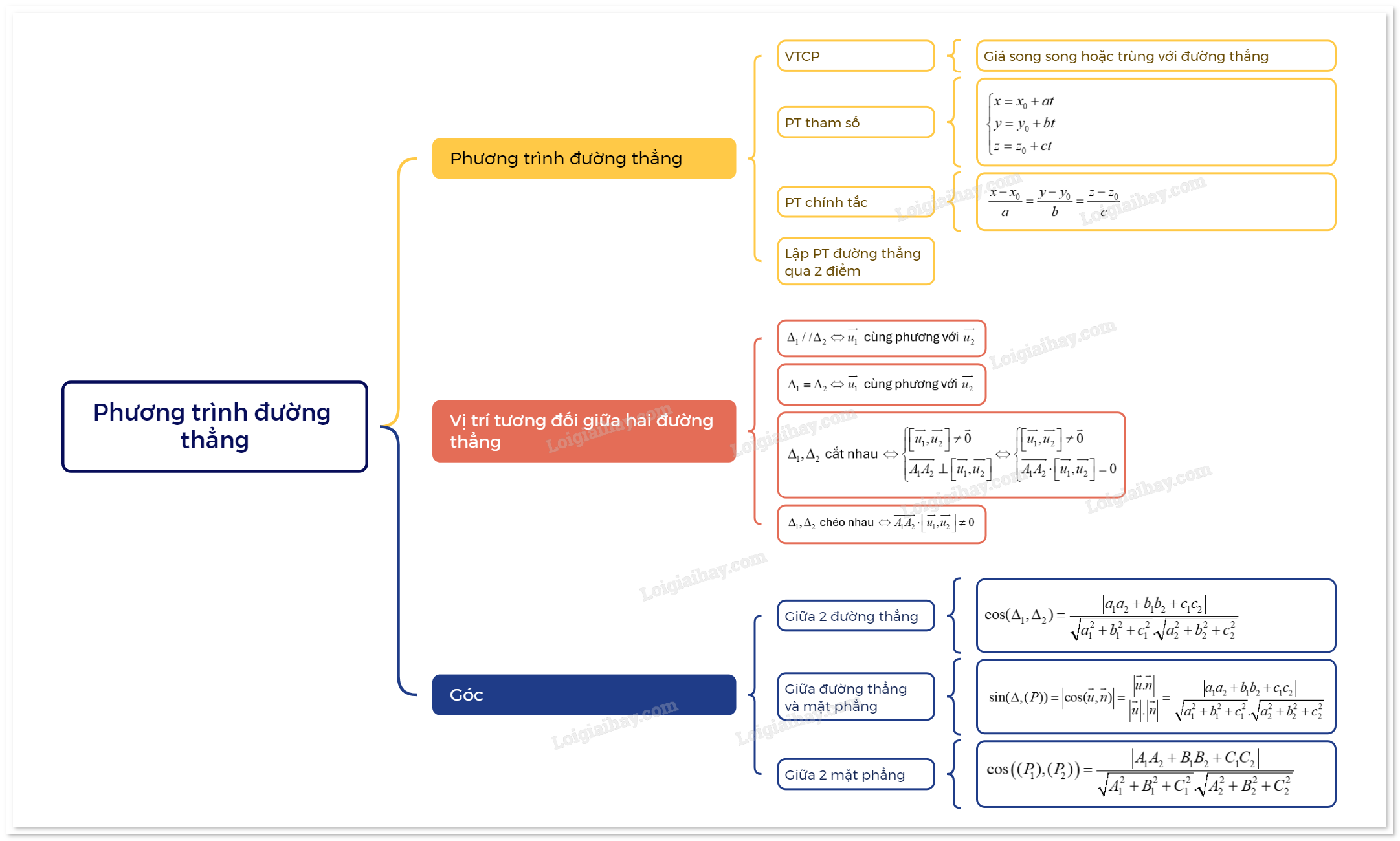
Tổng hợp đề thi học kì 2 lớp 12 tất cả các môn - Cánh diều

Toán - Văn - Anh - Hoá - Sinh - Sử - Địa

1. Phương trình đường thẳng

a) Vecto chỉ phương của đường thẳng

Vecto \(\overrightarrow u \ne \overrightarrow 0 \) được gọi là vecto chỉ phương của đường thẳng \(\Delta \) nếu giá của \(\overrightarrow u \) song song hoặc trùng với \(\Delta \).

b) Phương trình tham số của đường thẳng

Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\). Hệ phương trình:

\(\left\{ \begin{array}{l}x = {x_0} + at\\y = {y_0} + bt\\z = {z_0} + ct\end{array} \right.\)

được gọi là phương trình tham số của đường thẳng \(\Delta \) (t là tham số, \(t \in R\)).

c) Phương trình chính tắc của đường thẳng

Trong không gian Oxyz, cho đường thẳng \(\Delta \) đi qua điểm \(A({x_0};{y_0};{z_0})\) và có vecto chỉ phương \(\overrightarrow u = (a;b;c)\) với a, b, c là các số khác 0.

Hệ phương trình

\(\frac{{x - {x_0}}}{a} = \frac{{y - {y_0}}}{b} = \frac{{z - {z_0}}}{c}\)

được gọi là phương trình chính tắc của đường thẳng \(\Delta \).

d) Lập phương trình đường thẳng đi qua hai điểm

Trong không gian Oxyz, cho hai điểm phân biệt \({A_1}({x_1};{y_1};{z_1})\) và \({A_2}({x_2};{y_2};{z_2})\). Đường thẳng \({A_1}{A_2}\) có vecto chỉ phương \(\overrightarrow {{A_1}{A_2}} = ({x_2} - {x_1};{y_2} - {y_1};{z_2} - {z_1})\).

- Đường thẳng \({A_1}{A_2}\) có phương trình tham số là \(\left\{ \begin{array}{l}x = {x_1} + ({x_2} - {x_1})t\\y = {y_1} + ({y_2} - {y_1})t\\z = {z_1} + ({z_2} - {z_1})t\end{array} \right.\) \((t \in R)\).

- Trong trường hợp \({x_1} \ne {x_2},{y_1} \ne {y_2},{z_1} \ne {z_2}\) thì đường thẳng \({A_1}{A_2}\) có phương trình chính tắc là: \(\frac{{x - {x_1}}}{{{x_2} - {x_1}}} = \frac{{y - {y_1}}}{{{y_2} - {y_1}}} = \frac{{z - {z_1}}}{{{z_2} - {z_1}}}\).

2. Vị trí tương đối giữa hai đường thẳng

Trong không gian Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({A_1}({x_1};{y_1};{z_1})\), \({A_2}({x_2};{y_2};{z_2})\) và tương ứng có vecto chỉ phương \(\overrightarrow {{u_1}} ({x_1};{y_1};{z_1})\), \(\overrightarrow {{u_2}} ({x_2};{y_2};{z_2})\). Khi đó:

+ \({\Delta _1}//{\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \notin {\Delta _2}\).

+ \({\Delta _1} \equiv {\Delta _2} \Leftrightarrow \overrightarrow {{u_1}} \) cùng phương với \(\overrightarrow {{u_2}} \) và \({A_1} \in {\Delta _2}\).

+ \({\Delta _1},{\Delta _2}\) cắt nhau \( \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} \bot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right]\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne \overrightarrow 0 \\\overrightarrow {{A_1}{A_2}} \cdot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] = 0\end{array} \right.\).

+ \({\Delta _1},{\Delta _2}\) chéo nhau \( \Leftrightarrow \overrightarrow {{A_1}{A_2}} \cdot \left[ {\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} } \right] \ne 0\).

3. Góc

a) Góc giữa hai đường thẳng

Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng \({\Delta _1},{\Delta _2}\) có vecto chỉ phương lần lượt là \(\overrightarrow {{u_1}} ({a_1};{b_1};{c_1})\), \(\overrightarrow {{u_2}} ({a_2};{b_2};{c_2})\). Khi đó, ta có:

\(\cos ({\Delta _1},{\Delta _2}) = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\)

b) Góc giữa đường thẳng và mặt phẳng

Trong không gian với hệ tọa độ Oxyz, cho đường thẳng \(\Delta \) có vecto chỉ phương lần lượt là \(\overrightarrow u ({a_1};{b_1};{c_1})\) và mặt phẳng (P) có vecto pháp tuyến \(\overrightarrow n ({a_2};{b_2};{c_2})\). Gọi \((\Delta ,(P))\) là góc giữa đường thẳng \(\Delta \) và mặt phẳng (P). Khi đó, ta có:

\(\sin (\Delta ,(P)) = \left| {\cos (\overrightarrow u ,\overrightarrow n )} \right| = \frac{{\left| {\overrightarrow u .\overrightarrow n } \right|}}{{\left| {\overrightarrow u } \right|.\left| {\overrightarrow n } \right|}} = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2} + {c_1}{c_2}} \right|}}{{\sqrt {a_1^2 + b_1^2 + c_1^2} .\sqrt {a_2^2 + b_2^2 + c_2^2} }}\)

c) Góc giữa hai mặt phẳng

Góc giữa hai mặt phẳng \(({P_1}),({P_2})\) là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó, kí hiệu là \(\left( {({P_1}),({P_2})} \right)\).

Trong không gian với hệ tọa độ Oxyz, cho hai mặt phẳng \(({P_1}),({P_2})\) có vecto pháp tuyến lần lượt là \(\overrightarrow {{n_1}} ({A_1};{B_1};{C_1})\), \(\overrightarrow {{n_2}} ({A_2};{B_2};{C_2})\). Khi đó, ta có:

\(\cos \left( {({P_1}),({P_2})} \right) = \frac{{\left| {{A_1}{A_2} + {B_1}{B_2} + {C_1}{C_2}} \right|}}{{\sqrt {A_1^2 + B_1^2 + C_1^2} .\sqrt {A_2^2 + B_2^2 + C_2^2} }}\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải mục 1 trang 65, 66, 67, 68, 69 SGK Toán 12 tập 2 - Cánh diều
Cho hình hộp ABCD.A’B’C’D’ (Hình 23). Giá của vectơ (overrightarrow {A'C'} ) và đường thẳng AC có vị trí tương đối như thế nào?
Giải mục 2 trang 69, 70, 71 SGK Toán 12 tập 2 - Cánh diều
Cho hai đường thẳng phân biệt \({\Delta _1},{\Delta _2}\) lần lượt đi qua các điểm \({M_1},{M_2}\) và tương ứng có vectơ chỉ phương là \(\overrightarrow {{u_1}} ,\overrightarrow {{u_2}} \) . a) Giả sử \({\Delta _1}\) song song với \({\Delta _2}\) (Hình 25). Các cặp vectơ sau có cùng phương hay không: \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{u_2}} \); \(\overrightarrow {{u_1}} \) và \(\overrightarrow {{M_1}{M_2}} \)?
Giải mục 3 trang 71, 72, 73, 74, 75 SGK Toán 12 tập 2 - Cánh diều
Cho hai mặt phẳng \(\left( {{P_1}} \right)\) và \(\left( {{P_2}} \right)\). Lấy hai đường thẳng \({\Delta _1},{\Delta _2}\) sao cho \({\Delta _1} \bot \left( {{P_1}} \right),\) \({\Delta _2} \bot \left( {{P_2}} \right)\) (Hình 31).
Giải bài tập 1 trang 78 SGK Toán 12 tập 2 - Cánh diều
Đường thẳng đi qua điểm A(3; 2; 5) nhận \(\overrightarrow u = \left( { - 2;8; - 7} \right)\) làm vectơ chỉ phương có phương trình tham số là:
Giải bài tập 2 trang 78 SGK Toán 12 tập 2 - Cánh diều
Đường thẳng đi qua điểm \(B\left( { - 1;3;6} \right)\) nhận \(\overrightarrow u = \left( {2; - 3;8} \right)\) làm vectơ chỉ phương có phương trình chính tắc là:
Giải bài tập 3 trang 78 SGK Toán 12 tập 2 - Cánh diều
Mặt phẳng \(\left( P \right):x - 2 = 0\) vuông góc với mặt phẳng nào sau đây? A. \(\left( {{P_1}} \right):x + 2 = 0\). B. \(\left( {{P_2}} \right):x + y - 2 = 0\). C. \(\left( {{P_3}} \right):z - 2 = 0\). D. \(\left( {{P_4}} \right):x + z - 2 = 0\).
Giải bài tập 4 trang 78 SGK Toán 12 tập 2 - Cánh diều
Cho đường thẳng \(\Delta \) có phương trình tham số \(\left\{ \begin{array}{l}x = 1 - t\\y = 3 + 2t\\z = - 1 + 3t\end{array} \right.\)(t là tham số). a) Chỉ ra tọa độ hai điểm thuộc đường thẳng \(\Delta \). b) Điểm nào trong các điểm \(C\left( {6; - 7; - 16} \right),D\left( { - 3;11; - 11} \right)\) thuộc đường thẳng \(\Delta \)?
Giải bài tập 5 trang 78, 79 SGK Toán 12 tập 2 - Cánh diều
Viết phương trình tham số và phương trình chính tắc của đường thẳng \(\Delta \) trong mỗi trường hợp sau: a) \(\Delta \) đi qua điểm \(A\left( { - 1;3;2} \right)\) và có vectơ chỉ phương \(\overrightarrow u = \left( { - 2;3;4} \right)\). b) \(\Delta \) đi qua hai điểm \(M\left( {2; - 1;3} \right)\) và \(N\left( {3;0;4} \right)\).
Giải bài tập 6 trang 79 SGK Toán 12 tập 2 - Cánh diều
Xác định vị trí tương đối của hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau: a) \({\Delta _1}:\frac{{x - 1}}{2} = \frac{{y - 2}}{1} = \frac{{z - 3}}{{ - 1}}\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 11 - 6t\\y = - 6 - 3t\\z = 10 + 3t\end{array} \right.\) (t là tham số); b) \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + 3t\\y = 2 + 4t\\z = 3 + 5t\end{array} \right.\) (t là tham số) và \({\Delta _2}:\frac{{x + 3}}{1} = \frac{{y + 6}}{2} = \frac{{z - 15}}{{ - 3}}\)
Giải bài tập 7 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa hai đường thẳng \({\Delta _1},{\Delta _2}\) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ): a) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + {t_1}\\y = 4 + \sqrt 3 {t_1}\\z = 0\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = - 1 + \sqrt 3 {t_2}\\y = 4 + {t_2}\\z = 5\end{array} \right.\) (\({t_1},{t_2}\) là tham số); b) \({\Delta _1}:\left\{ \begin{array}{l}x = - 1 + 2t\\y = 3 + t\\z = 4 - t\end{array} \right.\) (t là tham số) và \({\Del
Giải bài tập 8 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa đường thẳng \(\Delta \) và mặt phẳng (P) trong mỗi trường hợp sau (làm tròn kết quả đến hàng đơn vị của độ): a) \(\Delta :\left\{ \begin{array}{l}x = 1 + \sqrt 3 t\\y = 2\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):\sqrt 3 x + z - 2 = 0\); b) \(\Delta :\left\{ \begin{array}{l}x = 1 + t\\y = 2 - t\\z = 3 + t\end{array} \right.\) (t là tham số) và \(\left( P \right):x + y + z - 4 = 0\).
Giải bài tập 9 trang 79 SGK Toán 12 tập 2 - Cánh diều
Tính góc giữa hai mặt phẳng \(\left( {{P_1}} \right):x + y + 2z - 1 = 0\) và \(\left( {{P_2}} \right):2x - y + z - 2 = 0\).
Giải bài tập 10 trang 80 SGK Toán 12 tập 2 - Cánh diều
Trong không gian với hệ tọa độ Oxyz, cho hình chóp S. ABCD có các đỉnh lần lượt là (Sleft( {0;0;frac{{asqrt 3 }}{2}} right),Aleft( {frac{a}{2};0;0} right),Bleft( { - frac{a}{2};0;0} right),Cleft( { - frac{a}{2};a;0} right),Dleft( {frac{a}{2};a;0} right)) với (a > 0) (Hình 36).
Giải bài tập 11 trang 80 SGK Toán 12 tập 2 - Cánh diều
Trong không gian với hệ tọa độ Oxyz (đơn vị trên mỗi trục tọa độ là kilômét), một máy bay đang ở vị trí \(A\left( {3,5; - 2;0,4} \right)\) và sẽ hạ cánh ở vị trí \[B\left( {3,5;5,5;0} \right)\] trên đường băng EG (Hình 37).