 Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo | Giải toán lớp 12 Chân trời sáng tạo
 Bài 2. Phương trình đường thẳng trong không gian - Toán..
Bài 2. Phương trình đường thẳng trong không gian - Toán..
Giải mục 3 trang 53, 54, 55, 65, 57, 58, 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
Cho hai đường thẳng (d) và (d') có vectơ chỉ phương lần lượt là (vec a = left( {2;1;3} right)) và (vec a' = left( {3;2; - 8} right)).
HĐ8
Trả lời câu hỏi Hoạt động 8 trang 53 SGK Toán 12 Chân trời sáng tạo
Cho hai đường thẳng \(d\) và \(d'\) có vectơ chỉ phương lần lượt là \(\vec a = \left( {2;1;3} \right)\) và \(\vec a' = \left( {3;2; - 8} \right)\).
a) Nhắc lại định nghĩa góc giữa hai đường thẳng \(d\) và \(d'\) trong không gian.
b) Vectơ \(\vec b = \left( { - 2;; - 1; - 3} \right)\) có phải là một vectơ chỉ phương của \(d\) không?
c) Giải thích tại sao ta lại có đẳng thức \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Nêu cách tìm côsin của góc giữa hai đường thẳng theo côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa hai đường thẳng trong không gian đã được học ở các lớp dưới.
b) Kiểm tra xem \(\vec b\) có cùng phương với vectơ \(\vec a\) không.
c) Do góc của hai đường thẳng lớn nhất là 90 độ, còn góc giữa hai vectơ lớn nhất là 180 độ.
d) Từ câu c, rút ra kết luận.
Lời giải chi tiết:
a) Góc giữa hai đường thẳng \(d\) và \(d'\) là góc giữa hai đường thẳng \(\Delta \) và \(\Delta '\) cùng đi qua một điểm và tương ứng song song (hoặc trùng) với \(d\) và \(d'\).
b) Ta có \(\vec b = \left( { - 2; - 1; - 3} \right) = - \vec a\) nên \(\vec b\) cũng là một vectơ chỉ phương của đường thẳng \(d\).
c) Do \(\vec a\) và \(\vec a'\) lần lượt là các vectơ chỉ phương của \(d\) và \(d'\), nên ta có \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right|\).
Ta có \(\vec a\) và \(\vec b\) là hai vectơ đối nhau, nên ta có \(\left( {\vec a,\vec a'} \right)\) và \(\left( {\vec b,\vec a'} \right)\) là hai góc bù nhau. Suy ra \(\left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
Như vậy \(\cos \left( {d,d'} \right) = \left| {\cos \left( {\vec a,\vec a'} \right)} \right| = \left| {\cos \left( {\vec b,\vec a'} \right)} \right|\).
d) Từ câu c, ta có côsin của góc giữa hai đường thẳng trong không gian là giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương của hai đường thẳng đó.
TH9
Trả lời câu hỏi Thực hành 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai đường thẳng \(d\) và \(d'\) trong mỗi trường hợp sau:
a) \(d:\frac{{x - 7}}{3} = \frac{y}{5} = \frac{{z - 11}}{4}\) và \(d':\frac{{x - 3}}{2} = \frac{{y + 6}}{5} = \frac{{z - 1}}{{ - 4}}.\)
b) \(d:\frac{{x + 9}}{3} = \frac{{y + 4}}{6} = \frac{{z + 1}}{6}\) và \(d':\left\{ \begin{array}{l}x = 9 - 10t\\y = 7 - 10t\\z = 15 + 5t\end{array} \right.\).
c) \(d:\left\{ \begin{array}{l}x = 23 + 2t\\y = 57 + t\\z = 19 - 5t\end{array} \right.\) và \(d':\left\{ \begin{array}{l}x = 24 + t'\\y = 6 + t'\\z = t'\end{array} \right.\).
Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
a) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;5;4} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {2;5; - 4} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.2 + 5.5 + 4.\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {5^2} + {4^2}} .\sqrt {{2^2} + {5^2} + {{\left( { - 4} \right)}^2}} }} = \frac{{\sqrt {10} }}{{10}}\).
Suy ra \(\left( {d,d'} \right) \approx {71^o}34'\).
b) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {3;6;6} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( { - 10; - 10;5} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {3.\left( { - 10} \right) + 6.\left( { - 10} \right) + 6.5} \right|}}{{\sqrt {{3^2} + {6^2} + {6^2}} .\sqrt {{{\left( { - 10} \right)}^2} + {{\left( { - 10} \right)}^2} + {5^2}} }} = \frac{4}{9}\).
Suy ra \(\left( {d,d'} \right) \approx {63^o}37'\).
c) Đường thẳng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 5} \right)\).
Đường thẳng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {1;1;1} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.1 + 1.1 + \left( { - 5} \right).1} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 5} \right)}^2}} .\sqrt {{1^2} + {1^2} + {1^2}} }} = \frac{{\sqrt {10} }}{{15}}\).
Suy ra \(\left( {d,d'} \right) \approx {77^o}50'\).
VD5
Trả lời câu hỏi Vận dụng 5 trang 55 SGK Toán 12 Chân trời sáng tạo
Trên một phần mềm đã thiết kế sân khấu 3D trong không gian \(Oxyz\). Tính góc giữa hai tia sáng có phương trình lần lượt là: \(d:\frac{x}{2} = \frac{y}{1} = \frac{z}{{ - 1}}\) và \(d':\frac{{x - 1}}{3} = \frac{{y - 1}}{3} = \frac{{z - 1}}{9}\) (Hình 11).

Phương pháp giải:
Chỉ ra các vectơ chỉ phương của các đường thẳng, tính giá trị tuyệt đối của côsin của góc giữa hai vectơ chỉ phương đó, từ đó suy ra góc giữa hai đường thẳng trong không gian.
Lời giải chi tiết:
Tia sáng \(d\) có một vectơ chỉ phương là \(\vec a = \left( {2;1; - 1} \right)\).
Tia sáng \(d'\) có một vectơ chỉ phương là \(\vec a' = \left( {3;3;9} \right)\).
Ta có \(\cos \left( {d,d'} \right) = \frac{{\left| {2.3 + 1.3 + \left( { - 1} \right).9} \right|}}{{\sqrt {{2^2} + {1^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{3^2} + {3^2} + {9^2}} }} = 0\).
Suy ra \(\left( {d,d'} \right) = {90^o}\).
HĐ9
Trả lời câu hỏi Hoạt động 9 trang 55 SGK Toán 12 Chân trời sáng tạo
Cho đường thẳng \(d\) có vectơ chỉ phương là \(\vec a = \left( {{a_1};{a_2};{a_3}} \right)\) và mặt phẳng \(\left( P \right)\) có vectơ pháp tuyến \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\). Biết \(d\) cắt \(\left( P \right)\) tại điểm \(N\) và hình chiếu vuông góc của \(d\) lên \(\left( P \right)\) là đường thẳng \(d'\). Qua \(N\) vẽ đường thẳng \(\Delta \) vuông góc với \(\left( P \right)\) (Hình 12).
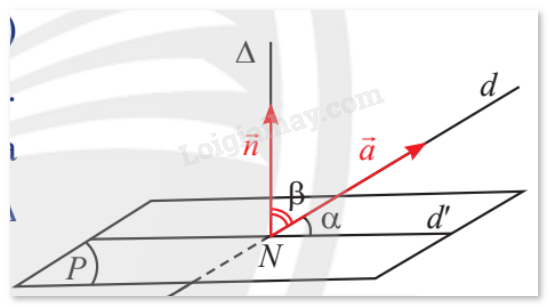
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.
b) Có nhận xét gì về số đo hai góc \(\alpha = \left( {d,d'} \right)\); \(\beta = \left( {\Delta ,d} \right)\)?
c) Giải thích tại sao ta lại có đẳng thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\).
Phương pháp giải:
a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng đã được học ở các lớp dưới.
b) Chỉ ra rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}\).
c) Từ câu b, rút ra kết luận.
Lời giải chi tiết:
a) Nếu đường thẳng \(a\) vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là \({90^o}\).
Nếu đường thẳng \(a\) không vuông góc với mặt phẳng \(\left( P \right)\) thì góc giữa đường thẳng \(a\) và mặt phẳng \(\left( P \right)\) là góc giữa đường thẳng \(a\) và hình chiếu \(a'\) của \(a\) trên \(\left( P \right).\)
b) Nhìn vào hình vẽ, ta thấy rằng hai góc \(\alpha \) và \(\beta \) có tổng số đo là \({90^o}.\)
c) Do \(\alpha + \beta = {90^o}\) nên ta có \(\sin \alpha = \cos \beta .\)
Ta có \(d'\) là hình chiếu vuông góc của \(d\) lên \(\left( P \right)\), nên \(\alpha = \left( {d,d'} \right) = \left( {d,\left( P \right)} \right).\)
Ta có \(\beta = \left( {\Delta ,d} \right)\) nên \(\cos \beta = \cos \left( {\Delta ,d} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|\). (Vì \(\vec a\) và \(\vec n\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(\Delta \)).
Mà \(\sin \alpha = \cos \beta \) nên \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
TH10
Trả lời câu hỏi Thực hành 10 trang 56 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa đường thẳng \(d\) và mặt phẳng \(\left( P \right)\) trong mỗi trường hợp sau:
a) \(d:\left\{ \begin{array}{l}x = 11 + 3t\\y = - 11 + t\\z = - 21 - 2t\end{array} \right.\) và \(\left( P \right):6x + 2y - 4z + 7 = 0.\)
b) \(d:\frac{{x - 3}}{2} = \frac{{y + 4}}{4} = \frac{{z - 5}}{2}\) và \(\left( P \right):2x + 2y - 4z + 1 = 0.\)
c) \(d:\frac{{x + 3}}{4} = \frac{{y + 5}}{4} = \frac{{z + 11}}{2}\) và \(\left( P \right):2y - 4z + 7 = 0.\)
Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của \(d\) và vectơ pháp tuyến \(\vec n\) của \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
a) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {3;1; - 2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {6;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {3.6 + 1.2 + \left( { - 2} \right).\left( { - 4} \right)} \right|}}{{\sqrt {{3^2} + {1^2} + {{\left( { - 2} \right)}^2}} .\sqrt {{6^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 1\).
Suy ra \(\left( {d,\left( P \right)} \right) = {90^o}\).
b) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {2;4;2} \right)\).
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {2;2; - 4} \right)\).
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {2.2 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{2^2} + {4^2} + {2^2}} .\sqrt {{2^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = \frac{1}{6}\).
Suy ra \(\left( {d,\left( P \right)} \right) \approx {9^o}36'\).
c) Một vectơ chỉ phương của đường thẳng \(d\) là \(\vec a = \left( {4;4;2} \right).\)
Một vectơ pháp tuyến của mặt phẳng \(\left( P \right)\) là \(\vec n = \left( {0;2; - 4} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {4.0 + 4.2 + 2.\left( { - 4} \right)} \right|}}{{\sqrt {{4^2} + {4^2} + {2^2}} .\sqrt {{0^2} + {2^2} + {{\left( { - 4} \right)}^2}} }} = 0.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {0^o}.\)
VD6
Trả lời câu hỏi Vận dụng 6 trang 56 SGK Toán 12 Chân trời sáng tạo
Đề bài:
Trên một sân khấu đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa tia sáng có phương trình \(d:\left\{ \begin{array}{l}x = 2\\y = 1 + t\\z = 1 + t\end{array} \right.\) và măt sàn sân khấu có phương trình \(z = 0.\)

Phương pháp giải:
Xác định vectơ chỉ phương \(\vec a\) của tia sáng \(d\) và vectơ pháp tuyến \(\vec n\) của mặt sân khấu \(\left( P \right)\). Sau đó sử dụng công thức \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right|.\)
Lời giải chi tiết:
Một vectơ chỉ phương của tia sáng \(d\) là \(\vec a = \left( {0;1;1} \right)\).
Một vectơ pháp tuyến của mặt sân khấu \(\left( P \right)\) là
\(\vec n = \left( {0;0;1} \right).\)
Ta có \(\sin \left( {d,\left( P \right)} \right) = \left| {\cos \left( {\vec a,\vec n} \right)} \right| = \frac{{\left| {0.0 + 1.0 + 1.1} \right|}}{{\sqrt {{0^2} + {1^2} + {1^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{\sqrt 2 }}{2}.\)
Suy ra \(\left( {d,\left( P \right)} \right) = {45^o}.\)
HĐ10
Trả lời câu hỏi Hoạt động 10 trang 57 SGK Toán 12 Chân trời sáng tạo
Cho hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) có vectơ pháp tuyến lần lượt là \(\vec n = \left( {{n_1};{n_2};{n_3}} \right)\), \(\vec n' = \left( {{n_1}';{n_2}';{n_3}'} \right)\) (Hình 14).
Gọi \(d\) và \(d'\) là hai đường thẳng lần lượt vuông góc với \(\left( P \right)\) và \(\left( {P'} \right)\). Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\). So sánh \(\cos \left( {\left( P \right),\left( {P'} \right)} \right)\) và \(\cos \left( {\vec n,\vec n'} \right).\)
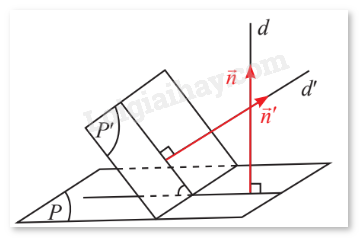
Phương pháp giải:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), từ đó rút ra kết luận.
Lời giải chi tiết:
Góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) là góc giữa hai đường thẳng \(d\) và \(d'\), nên suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = \left( {d,d'} \right).\)
Như vậy \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \cos \left( {d,d'} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\). (Do \(\vec n\) và \(\vec n'\) lần lượt là các vectơ chỉ phương của các đường thẳng \(d\) và \(d'.\)
TH11
Trả lời câu hỏi Thực hành 11 trang 58 SGK Toán 12 Chân trời sáng tạo
Tính góc giữa hai mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\) trong mỗi trường hợp sau:
a) \(\left( P \right):3x + 7y - z + 4 = 0\) và \(\left( {P'} \right):x + y - 10z + 2025 = 0.\)
b) \(\left( P \right):x - 2y + z + 9 = 0\) và \(\left( {P'} \right):3x + y - 5z + 2024 = 0.\)
c) \(\left( P \right):x + z + 3 = 0\) và \(\left( {P'} \right):3y + 3z + 5 = 0.\)
Phương pháp giải:
Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( P \right)\) và \(\left( {P'} \right)\), sau đó sử dụng công thức \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \left| {\cos \left( {\vec n,\vec n'} \right)} \right|\).
Lời giải chi tiết:
a) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {3;7; - 1} \right)\) và \(\vec n' = \left( {1;1; - 10} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {3.1 + 7.1 + \left( { - 1} \right).\left( { - 10} \right)} \right|}}{{\sqrt {{3^2} + {7^2} + {{\left( { - 1} \right)}^2}} .\sqrt {{1^2} + {1^2} + {{\left( { - 10} \right)}^2}} }} = \frac{{20}}{{\sqrt {6018} }}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {75^o}3'.\)
b) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\overrightaroww n = \left( {1; - 2;1} \right)\) và \(\overrightaroww n' = \left( {3;1; - 5} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.3 + \left( { - 2} \right).1 + 1.\left( { - 5} \right)} \right|}}{{\sqrt {{1^2} + {{\left( { - 2} \right)}^2} + {1^2}} .\sqrt {{3^2} + {1^2} + {{\left( { - 5} \right)}^2}} }} = \frac{{2\sqrt {210} }}{{105}}\).
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) \approx {73^o}59'.\)
c) \(\left( P \right)\) và \(\left( {P'} \right)\) có các vectơ pháp tuyến lần lượt là \(\vec n = \left( {1;0;1} \right)\) và \(\vec n' = \left( {0;3;3} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( {P'} \right)} \right) = \frac{{\left| {1.0 + 0.3 + 1.3} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {3^2} + {3^2}} }} = \frac{1}{2}.\)
Suy ra \(\left( {\left( P \right),\left( {P'} \right)} \right) = {30^o}.\)
TH12
Trả lời câu hỏi Thực hành 12 trang 59 SGK Toán 12 Chân trời sáng tạo
Trong không gian \(Oxyz\), cho hình hộp chữ nhật \(ABCD.A'B'C'D'\). Cho biết \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Tính góc giữa:
a) hai đường thẳng \(AC\) và \(BA'.\)
b) hai mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right).\)
c) đường thẳng \(AC'\) và mặt phẳng \(\left( {A'BD} \right).\)
Phương pháp giải:
a) Xác định các vectơ chỉ phương của các đường thẳng \(AC\) và \(BA'\), côsin góc giữa hai đường thẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
b) Xác định các vectơ pháp tuyến của các mặt phẳng \(\left( {BB'D'D} \right)\) và \(\left( {AA'C'C} \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
c) Xác định vectơ chỉ phương của đường thẳng \(AC'\) và vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\), sin góc giữa đường thẳng và mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
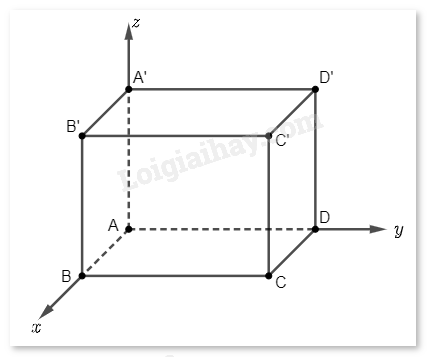
a) Ta có \(A\left( {0;0;0} \right)\), \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\), suy ra \(C\left( {1;5;0} \right).\)
Suy ra \(\overrightarrow {AC} = \left( {1;5;0} \right)\) và \(\overrightarrow {BA'} = \left( { - 1;0;3} \right).\)
Ta có \(\cos \left( {AC,BA'} \right) = \left| {\cos \left( {\overrightarrow {AC} ,\overrightarrow {BA'} } \right)} \right| \)
\(= \frac{{\left| {1.\left( { - 1} \right) + 5.0 + 0.3} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} .\sqrt {{{\left( { - 1} \right)}^2} + {0^2} + {3^2}} }} = \frac{{\sqrt {65} }}{{130}}\).
Vậy \(\left( {AC,BA'} \right) \approx {86^o}27'.\)
b) Ta có \(BB' \bot AC\) và \(DB \bot AC\) nên \(\overrightarrow {AC} = \left( {1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {BB'D'D} \right).\)
Ta có \(CC' \bot BD\) và \(AC \bot BD\) nên \(\overrightarrow {BD} = \left( { - 1;5;0} \right)\) là một vectơ pháp tuyến của mặt phẳng \(\left( {AA'C'C} \right).\)
Như vậy, \(\cos \left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) = \left| {\cos \left( {\overrightarrow {BD} ,\overrightarrow {AC} } \right)} \right| \)
\(= \frac{{\left| {1.\left( { - 1} \right) + 5.5 + 0.0} \right|}}{{\sqrt {{1^2} + {5^2} + {0^2}} \sqrt {{{\left( { - 1} \right)}^2} + {5^2} + {0^2}} }} = \frac{{12}}{{13}}.\)
Suy ra \(\left( {\left( {BB'D'D} \right),\left( {AA'C'C} \right)} \right) \approx {22^o}37'\).
c) Ta có \(C'\left( {1;5;3} \right) \Rightarrow \overrightarrow {AC'} = \left( {1;5;3} \right).\)
Ta có \(B\left( {1;0;0} \right)\), \(D\left( {0;5;0} \right)\), \(A'\left( {0;0;3} \right)\). Suy ra mặt phẳng \(\left( {A'BD} \right)\) có một cặp vectơ chỉ phương là \(\overrightarrow {A'B} \left( {1;0; - 3} \right)\) và \(\overrightarrow {A'D} \left( {0;5; - 3} \right)\). Suy ra một vectơ pháp tuyến của mặt phẳng \(\left( {A'BD} \right)\) là \(\vec n = \left[ {\overrightarrow {AB} ,\overrightarrow {AD} } \right] = \left( {15;3;5} \right).\)
Ta có \(\sin \left( {AC',\left( {A'BD} \right)} \right) = \left| {\cos \left( {\overrightarrow {AC'} ,\vec n} \right)} \right| \)
\(= \frac{{\left| {1.15 + 5.3 + 3.5} \right|}}{{\sqrt {{1^2} + {5^2} + {3^2}} .\sqrt {{{15}^2} + {3^2} + {5^2}} }} = \frac{{9\sqrt {185} }}{{259}}.\)
Suy ra \(\left( {AC',\left( {A'BD} \right)} \right) \approx {28^o}12'.\)
VD7
Trả lời câu hỏi Vận dụng 7 trang 59 SGK Toán 12 Chân trời sáng tạo
Để làm thí nghiệm về chuyển động trong mặt phẳng nghiêng, người làm thí nghiệm đã thiết lập sẵn một hệ toạ độ \(Oxyz\). Tính góc giữa mặt phẳng nghiêng \(\left( P \right):4x + 11z + 5 = 0\) và mặt sàn \(\left( Q \right):z - 1 = 0.\)
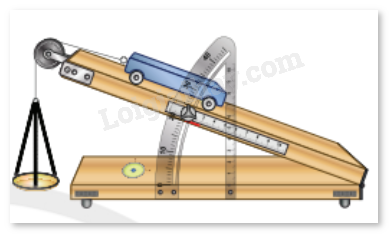
Phương pháp giải:
Xác định các vectơ pháp tuyến của mặt phẳng nghiêng \(\left( P \right)\) và mặt sàn \(\left( Q \right)\), côsin góc giữa hai mặt phẳng bằng giá trị tuyệt đối của côsin góc giữa hai vectơ đó.
Lời giải chi tiết:
Mặt phẳng nghiêng \(\left( P \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( P \right)}}} = \left( {4;0;11} \right).\)
Mặt sàn \(\left( Q \right)\) có một vectơ pháp tuyến là \(\overrightarrow {{n_{\left( Q \right)}}} = \left( {0;0;1} \right).\)
Ta có \(\cos \left( {\left( P \right),\left( Q \right)} \right) = \left| {\cos \left( {\overrightarrow {{n_{\left( P \right)}}} ,\overrightarrow {{n_{\left( Q \right)}}} } \right)} \right| \)
\(= \frac{{\left| {4.0 + 0.0 + 11.1} \right|}}{{\sqrt {{4^2} + {0^2} + {{11}^2}} .\sqrt {{0^2} + {0^2} + {1^2}} }} = \frac{{11}}{{\sqrt {137} }}.\)
Suy ra \(\left( {\left( P \right),\left( Q \right)} \right) \approx {19^o}59'.\)
- Giải bài tập 1 trang 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 2 trang 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 3 trang 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 4 trang 59 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải bài tập 5 trang 60 SGK Toán 12 tập 2 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 75 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 69 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 61 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 43 SGK Toán 12 tập 2 - Chân trời sáng tạo
- Giải câu hỏi mở đầu trang 32 SGK Toán 12 tập 2 - Chân trời sáng tạo












Danh sách bình luận