Giải mục 2 trang 90, 91, 92, 93 SGK Toán 11 tập 1 - Chân trời sáng tạo

Hoạt động 2

Quan sát Hình 5 và cho biết muốn gác một cây sao tập nhảy cao, người ta cần dựa nó vào mấy điểm trên hai cọc đỡ.

Phương pháp giải:

Quan sát và trả lời câu hỏi.

Lời giải chi tiết:

Từ hình ảnh ta thấy muốn gác một cây sao tập nhảy cao, người ta cần dựa nó vào một điểm trên mỗi cọc đỡ.

Thực hành 2

Cho bốn điểm \(A,B,C,D\) phân biệt, trong đó không có ba điểm nào thẳng hàng. Có bao nhiêu đường thắng đi qua hai trong bốn điểm đã cho?

Phương pháp giải:

Dựa vào tính chất 1: Có một và chỉ một đường thẳng đi qua hai điểm phân biệt cho trước.

Lời giải chi tiết:

Do qua hai điểm phân biệt chỉ có một đường thẳng nên qua bốn điểm phân biệt không thẳng hàng \(A,B,C,D\), ta xác định được sáu đường thẳng là \(AB,AC,A{\rm{D}},BC,B{\rm{D}}\) và \(C{\rm{D}}\).

Hoạt động 3

Quan sát Hình 7 và cho biết giá đỡ máy ảnh tiếp đất tại mấy điểm. Tại sao giá đỡ máy ảnh thường có ba chân?

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

‒ Giá đỡ máy ảnh tiếp đất tại ba điểm.

‒ Giá đỡ máy ảnh thường có ba chân để giữ được cân bằng và đỡ được máy ảnh bên trên.

Thực hành 3

Có bao nhiêu mặt phẳng đi qua ba đỉnh của tam giác \(MNP\)?

Phương pháp giải:

Dựa vào tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

Lời giải chi tiết:

Ba đỉnh của tam giác \(MNP\) không thẳng hàng nên chỉ có một mặt phẳng đi qua ba đỉnh của tam giác \(MNP\).

Hoạt động 4

Quan sát Hình 10 và cho biết người thợ mộc kiểm tra mặt bàn có phẳng hay không bằng một cây thước thẳng như thế nào.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

Người thợ mộc rê thước trên mặt bàn. Khi đó, nếu rê thước mà có 1 điểm thuộc cạnh thước nhưng không thuộc mặt bàn thì bàn đó chưa phẳng và ngược lại, nếu tất cả các điểm thuộc cạnh thước và mặt bàn thì mặt bàn đó phẳng.

Thực hành 4

Cho mặt phẳng \(\left( Q \right)\) đi qua bốn đỉnh của tứ giác \(ABCD\). Các điểm nằm trên các đường chéo của tứ giác \(ABCD\) có thuộc mặt phẳng \(\left( Q \right)\) không? Giải thích.

Phương pháp giải:

Áp dụng các tính chất :

‒ Tính chất 2: Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng cho trước.

‒ Tính chất 3: Nếu một đường thẳng có hai điểm phân biệt thuộc một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.

Lời giải chi tiết:

Áp dụng tính chất 2, ta có mặt phẳng \(\left( Q \right)\) là mặt phẳng duy nhất đi qua bốn điểm \(A,B,C,D\).

Áp dụng tính chất 3, ta có mọi điểm nằm trên các đường chéo \(AC\) và \(BD\) của tứ giác  \(ABCD\) đều thuộc mặt phẳng \(\left( Q \right)\).

Hoạt động 5

Quan sát Hình 13 và cho biết bốn đỉnh \(A,B,C,D\) của cái bánh giò có cùng nằm trên một mặt phẳng hay không.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

Bốn đỉnh \(A,B,C,D\) của cái bánh giò không cùng nằm trên một mặt phẳng.

Thực hành 5

Cho tam giác \(MNP\) và cho điểm \(O\) không thuộc mặt phẳng chứa ba điểm \(M,N,P\). Tìm các mặt phẳng phân biệt được xác định từ bốn điểm \(M,N,P,O\).

Phương pháp giải:

Dựa vào tính chất 4: Tồn tại bốn điểm không cùng nằm trên một mặt phẳng.

Lời giải chi tiết:

Bốn điểm \(M,N,P,O\) là bốn điểm không cùng nằm trên một mặt phẳng trong không gian (tồn tại theo tính chất 4). Ta xác định được bốn mặt phẳng phân biệt là: \(\left( {MNP} \right)\), \(\left( {MNO} \right),\left( {MPO} \right),\left( {NPO} \right)\).

Hoạt động 6

Quan sát Hình 14 và mô tả phần giao nhau của hai bức tường.

Phương pháp giải:

Quan sát hình ảnh và trả lời câu hỏi.

Lời giải chi tiết:

Phần giao nhau của hai bức tường là một đường thẳng.

Thực hành 6

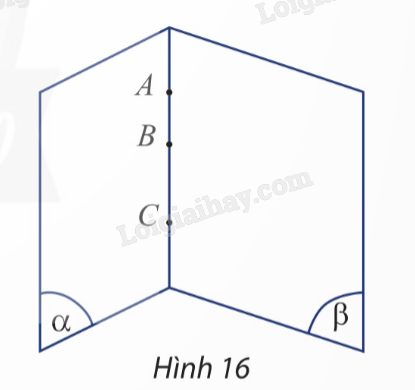
Cho \(A,B,C\) là ba điểm chung của hai mặt phẳng phân biệt \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) (Hình 16). Chứng minh \(A,B,C\) thẳng hàng.

Phương pháp giải:

Dựa vào tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.Dựa vào tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Lời giải chi tiết:

Ta có: \(A,B,C\) là ba điểm chung của hai mặt phẳng phân biệt \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) nên \(A,B,C\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( \alpha  \right)\) và \(\left( \beta  \right)\) (theo tính chất 5).

Vậy \(A,B,C\) thẳng hàng.

Hoạt động 7

Trong mặt phẳng \(\left( P \right)\), cho tam giác \(ABC\) có \(M,N\) lần lượt là trung điểm của các đoạn thẳng \(AB,AC\) (Hình 17). Tính tỉ số \(\frac{{MN}}{{BC}}\).

Phương pháp giải:

Áp dụng định lý đường trung bình của tam giác.

Lời giải chi tiết:

Xét tam giác \(ABC\). Ta có:

\(M\) là trung điểm của \(AB\).

\(N\) là trung điểm của \(AC\).

\( \Rightarrow MN\) là đường trung bình của tam giác \(ABC\)

\( \Rightarrow MN = \frac{1}{2}BC \Rightarrow \frac{{MN}}{{BC}} = \frac{1}{2}\)

Vận dụng 1

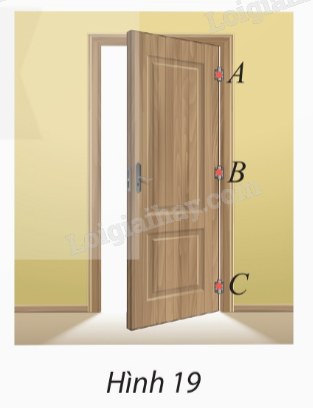
Tại sao muốn cánh cửa đóng mở được êm thì các điểm gắn bản lề \(A,B,C\) của cánh cửa và mặt tường (Hình 19) phải cùng nằm trên một đường thẳng?

Phương pháp giải:

Dựa vào tính chất 5: Nếu hai mặt phẳng phân biệt có một điểm chung thì chúng có một đường thẳng chung duy nhất chứa tất cả các điểm chung của hai mặt phẳng đó.

Lời giải chi tiết:

Do mặt tường và cánh cửa là hai mặt phẳng phân biệt nên theo tính chất 5, các điểm trên bản lề phải nằm trên một đường thẳng để mặt phẳng cánh cửa tiếp xúc với mặt phẳng tường qua 1 đường thẳng (chính là giao tuyến của mặt phẳng tường và mặt phẳng cánh cửa). Khi đó cánh cửa đóng mở được êm hơn.