 Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
 Bài 22. Hai đường thẳng vuông góc Toán 11 Kết nối tri t..
Bài 22. Hai đường thẳng vuông góc Toán 11 Kết nối tri t..
Giải mục 1 trang 28, 29 SGK Toán 11 tập 2 - Kết nối tri thức
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O'
HĐ1
Video hướng dẫn giải
Trong không gian, cho hai đường thẳng chéo nhau m và n. Từ hai điểm phân biệt O,O' tuỳ ý lần lượt kẻ các cặp đường thẳng a, b và a', b' tương ứng song song với m, n (H.7.2).
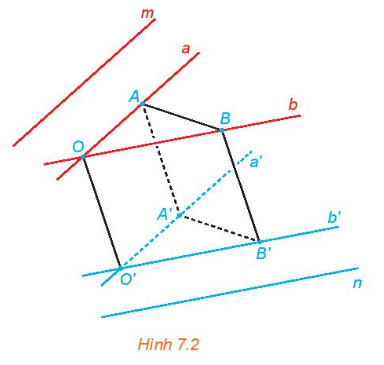
a) Mỗi cặp đường thẳng a, a và b, b' có cùng thuộc một mặt phẳng hay không?
b) Lấy các điểm A, B (khác O) tương ứng thuộc a, b. Đường thẳng qua A song song với OO' cắt a' tại A', đường thẳng qua B song song với OO' cắt b' tại B' Giải thích vì sao OAA'O', OBB'O', ABB'A' là các hình bình hành.
c) So sánh góc giữa hai đường thẳng a, b và góc giữa hai đường thẳng a', b'.
(Gợi ý: Áp dụng định lí côsin cho các tam giác OAB, O'A'B').
Phương pháp giải:
- Tứ giác có các cặp cạnh đối song song là hình bình hành.
- Định lí côsin \(\cos A = \frac{{{b^2} + {c^2} - {a^2}}}{{2ab}}\)
Lời giải chi tiết:
a) Mỗi cặp đường thẳng a, a' và b, b' cùng thuộc một mặt phẳng vì a // a', b // b'.
b) Ta có:
+) OA // O′A′; OO' // AA' nên OAA'O' là hình bình hành.
+) OB // O′B′; OO' // BB' nên OBB'O' là hình bình hành.
+) AB // A′B′ và OO' // AA'; OO' // BB' suy ra AA' // BB' nên ABB'A' là hình bình hành.
c) Áp dụng định lí côsin cho các tam giác OAB và O'A'B', ta có:
\(\cos \left( {a,b} \right) = \frac{{O{A^2} + O{B^2} - A{B^2}}}{{2.OA.OB}};\cos \left( {a',b'} \right) = \frac{{O'{{A'}^2} + O'{{B'}^2} - A'{{B'}^2}}}{{2.O'A'.O'B'}}\)
Vì O'A' = OA và O'B' = OB; AB = A'B' nên cos(a,b) = cos(a′,b′).
CH
Video hướng dẫn giải
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) và (a', b') có mối quan hệ gì?
Phương pháp giải:
Sử dụng Hoạt động 1 trang 28
Lời giải chi tiết:
Nếu a song song hoặc trùng với a' và b song song hoặc trùng với b' thì (a, b) = (a', b')
VD
Video hướng dẫn giải
Kim tự tháp Kheops là kim tự tháp lớn nhất trong các kim tự tháp ở Ai Cập, được xây dựng vào thế kỉ thứ 26 trước Công nguyên và là một trong bảy kì quan của thế giới cổ đại. Kim tự tháp có dạng hình chóp với đáy là hình vuông có cạnh dài khoảng 230 m, các cạnh bên bằng nhau và dài khoảng 219 m (kích thước hiện nay). (Theo britannica.com).
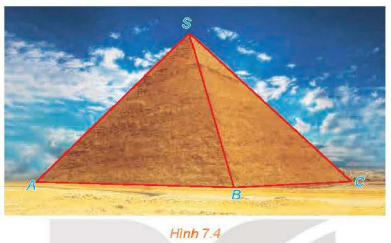
Tính (gần đúng) góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp (H.7.4).
Phương pháp giải:
Để xác định góc giữa hai đường thẳng chéo nhau a và b, ta có thể lấy một điểm O thuộc đường thẳng a và qua đó kẻ đường thẳng b' song song với b. Khi đó (a, b) = (a', b').
Lời giải chi tiết:
Vì AB // CD (ABCD là hình vuông) nên (SC, AB) = (SC, CD).
Xét tam giác SCD có: \(\cos \widehat {SCD} = \frac{{S{C^2} + C{D^2} - S{D^2}}}{{2SC.CD}} \)
\(= \frac{{{{219}^2} + {{230}^2} - {{219}^2}}}{{2.219.230}} = \frac{{115}}{{219}} \Rightarrow \widehat {SCD} \approx 58,{32^o}\).
Vậy góc tạo bởi cạnh bên SC và cạnh đáy AB của kim tự tháp bằng khoảng \(58,32^o\).
- Giải mục 2 trang 29, 30 SGK Toán 11 tập 2 - Kết nối tri thức
- Bài 7.1 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
- Bài 7.2 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
- Bài 7.3 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
- Bài 7.4 trang 30 SGK Toán 11 tập 2 – Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức












Danh sách bình luận