A. Hoạt động thực hành - Bài 104 : Ôn tập về phép cộng, phép trừ
Giải Bài 104 : Ôn tập về phép cộng, phép trừ phần hoạt động thực hành trang 111, 112, 113, 114 sách VNEN toán lớp 5 với lời giải dễ hiểu
Câu 1
Chơi trò chơi “Hái hoa toán học” :
– Mỗi nhóm cử đại diện hái một bông hoa, trên đó có ghi phép tính cộng, trừ với các số tự nhiên, phân số hoặc số thập phân. Cùng nhau tính và giải thích cách thực hiện.
Ví dụ :
– Nhóm nào tính nhanh, đúng, giải thích mạch lạc sẽ thắng cuộc.
Phương pháp giải:
- Muốn cộng (hoặc trừ) các số tự nhiên ta đặt tính sao cho các chữ số ở cùng hàng thẳng cột với nhau, sau đó tính theo thứ tự từ phải sang trái.
- Muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng hai phân số sau khi quy đồng.
- Muốn cộng (hoặc trừ) các số thập phân ta đặt tính sao cho các chữ số ở cùng hàng thẳng cột với nhau, dấu phẩy thẳng nhau, sau đó tính theo thứ tự từ phải sang trái.
Lời giải chi tiết:
Ví dụ :
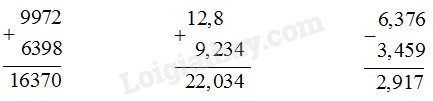
\(\dfrac{3}{8} + \dfrac{9}{5} = \dfrac{{15}}{{40}} + \dfrac{{72}}{{40}} = \dfrac{{87}}{{40}}\)
\(\dfrac{5}{7} - \dfrac{4}{9} = \dfrac{{45}}{{63}} - \dfrac{{28}}{{63}} = \dfrac{{17}}{{63}}\)
Câu 2
a) Đọc nội dung sau :
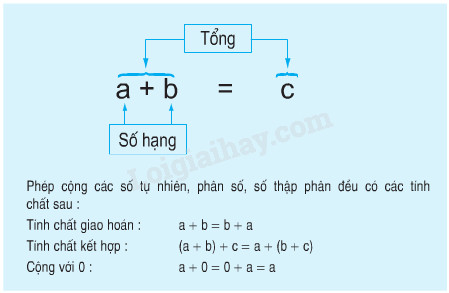
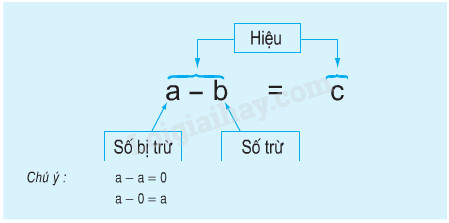
b) Lấy một ví dụ minh họa rồi giải thích cho các bạn nghe.
Phương pháp giải:
Đọc kĩ nội dung trong bảng rồi tự lấy ví dụ minh họa.
Lời giải chi tiết:
Lấy ví dụ phép cộng :
+) Tính chất giao hoán : a + b = b + a
Ví dụ : 40 + 60 = 60 + 40 = 100
+) Tính chất kết hợp : (a + b) + c = a + (b + c)
Ví dụ: (18 + 25) + 75 = 18 + (25 + 75) = 118
+) Cộng với 0 : a + 0 = 0 + a
Ví dụ: 45 + 0 = 0 + 45 = 45
Lấy ví dụ phép trừ :
+) 3579 – 3579 = 0
+) 1234 – 0 = 1234
Câu 3
Tính:

Phương pháp giải:
- Muốn cộng (hoặc trừ) các số tự nhiên ta đặt tính sao cho các chữ số ở cùng hàng thẳng cột với nhau, sau đó tính theo thứ tự từ phải sang trái.
- Muốn cộng hai phân số khác mẫu số ta quy đồng mẫu số hai phân số rồi cộng hai phân số sau khi quy đồng.
- Muốn cộng (hoặc trừ) các số thập phân ta đặt tính sao cho các chữ số ở cùng hàng thẳng cột với nhau, dấu phẩy thẳng nhau, sau đó tính theo thứ tự từ phải sang trái.
Lời giải chi tiết:
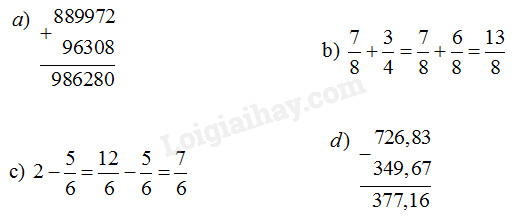
Câu 4
Tính rồi thử lại (theo mẫu) :

Phương pháp giải:
Muốn thử lại phép trừ ta có thể lấy hiệu cộng với số trừ, nếu được kết quả là số bị trừ thì phép tính làm đúng.
Lời giải chi tiết:

Câu 5
a) Vòi nước thứ nhất mỗi giờ chảy được \(\dfrac{1}{5}\) thể tích của bể, vòi nước thứ hai mỗi giờ chảy được \(\dfrac{3}{{10}}\) thể tích của bể. Hỏi khi cả hai vòi nước cùng chảy vào bể trong một giờ thì được bao nhiêu phần trăm thể tích của bể ?
b) Một mảnh đất hình chữ nhật có nửa chu vi là 75m, chiều rộng bằng \(\dfrac{2}{3}\) chiều dài. Tính diện tích mảnh đất đó.
Phương pháp giải:
a) - Tính số phần thể tích của bể mà hai vòi chảy được trong 1 giờ, tức là thực hiện tính \(\dfrac{1}{5}+\dfrac{3}{10} \).
- Đổi kết quả vừa tìm được dưới dạng tỉ số phần trăm.
b) - Tìm chiều dài, chiều rộng theo bài toán tìm hai số khi biết tổng và tỉ số của hai số đó.
- Tính diện tích ta lấy chiều dài nhân với chiều rộng (cùng một đơn vị đo).
Lời giải chi tiết:
a) Mỗi giờ cả hai vòi cùng chảy được số phần thể tích của bể là :
\(\dfrac{1}{5}+\dfrac{3}{10} = \dfrac{5}{10}\) (thể tích của bể)
\(\dfrac{5}{10}=0,5 = 50\%\)
Đáp số: \(50\%\) thể tích bể.
b) Ta có sơ đồ :
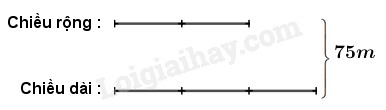
Theo sơ đồ, tổng số phần bằng nhau là :
3 + 2 = 5 (phần)
Chiều rộng hình chữ nhật là :
75 : 5 × 2 = 30 (m)
Chiều dài hình chữ nhật là :
75 – 30 = 45 (m)
Diện tích hình chữ nhật là :
45 × 30 = 1350 (m2)
Đáp số : 1350m2.
Câu 6
a) \(\dfrac{2}{5} + \dfrac{3}{4}\,\,;\) \(\dfrac{7}{{12}} - \dfrac{2}{7} + \dfrac{1}{{12}}\,\,;\) \(\dfrac{{}}{{}}\) \(\dfrac{{12}}{{17}} - \dfrac{5}{{17}} - \dfrac{4}{{17}}\)
b) \(675,39 + 342,14;\) \(563,87 + 403,13 – 328,35\)
Phương pháp giải:
Biểu thức chỉ có phép cộng và phép trừ thì tính lần lượt từ trái sang phải.
Lời giải chi tiết:
a) \(\dfrac{2}{5} + \dfrac{3}{4} = \dfrac{8}{{20}} + \dfrac{{15}}{{20}} = \dfrac{{23}}{{20}}\,\,;\)
+) \(\dfrac{7}{{12}} - \dfrac{2}{7} + \dfrac{1}{{12}}\,\, = \dfrac{7}{{12}} + \dfrac{1}{{12}} - \dfrac{2}{7}\)
\( = \dfrac{8}{{12}} - \dfrac{2}{7} = \dfrac{2}{3} - \dfrac{2}{7} = \dfrac{{14}}{{21}} - \dfrac{6}{{21}}\)\( = \dfrac{8}{{21}};\)
+) \(\dfrac{{12}}{{17}} - \dfrac{5}{{17}} - \dfrac{4}{{17}} = \dfrac{7}{{17}} - \dfrac{4}{{17}} \)\(= \dfrac{3}{{17}}\)
b) \(675,39 + 342,14 = 1017,53;\)
+) \(563,87 + 403,13 \,– 328,35\) \(= 967-328,35= 638,65\)
Câu 7
Tính bằng cách thuận tiện nhất :

Phương pháp giải:
Áp dụng tính chất giao hoán và kết hợp của phép cộng để nhóm các số có tổng là số tròn trăm, tròn nghìn ... hoặc nhóm các phân số, số thập phân có tổng là số tự nhiên.
Lời giải chi tiết:

Câu 8
a) Không trực tiếp làm phép tính, em dự đoán kết quả tìm \(x\) :
\(x\) + 7,08 = 7,08 \(\dfrac{3}{5} + x = \dfrac{6}{{10}}\)
b) Tìm \(x\) :
\(x\) + 3,72 = 8,16 \(x\) – 0,25 = 3,148
Phương pháp giải:
a) Áp dụng tính chất: Số \(0\) cộng với số nào cũng bằng chính số đó.
b) Áp dụng các quy tắc :
- Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.
- Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ.
Lời giải chi tiết:
a) \(x\) + 7,08 = 7,08
\(x\) = 0 (vì 0 cộng với số nào cũng bằng chính số đó).
+) \(\dfrac{3}{5}+ x = \dfrac{6}{10}\)
Ta có : \(\dfrac{6}{10} =\dfrac{6:2}{10:2}= \dfrac{3}{5}\)
Từ đó ta có : \(\dfrac{3}{5} + x = \dfrac{3}{5}\).
Suy ra \(x = 0\), vì \(0\) cộng với số nào cũng bằng chính số đó.
b) Tìm \(x\) :

Câu 9
Giải bài toán :
Một xã có 540,8 ha đất trồng lúa. Diện tích đất trồng hoa ít hơn diện tích đất trồng lúa 385,5ha. Tính tổng diện tích đất trồng lúa và trồng hoa của xã đó.
Phương pháp giải:
- Tính diện tích đất trồng hoa ta lấy diện tích đất trồng lúa trừ đi 385,5ha.
- Tính tổng diện tích đất trồng lúa và trồng hoa của xã đó ta lấy diện tích đất trồng lúa cộng với diện tích đất trồng hoa.
Lời giải chi tiết:
Tóm tắt
Trồng lúa: 540,8 ha
Trồng hoa: ít hơn 385,5 ha
Tổng diện tích: ...ha?
Bài giải
Diện tích đất trồng hoa là :
540,8 – 385,5 = 155,3 (ha)
Tổng diện tích đất trồng lúa và trồng hoa của xã đó là :
540,8 + 155,3 = 696,1 (ha)
Đáp số : 696,1ha.
Loigiaihay.com













Danh sách bình luận