Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Đề thi học kì 1 của các trường có lời giải – Mới nhất
Giải đề thi học kì 1 toán lớp 6 năm 2020 - 2021 phòng GD-ĐT Thị xã Bình Minh
Giải chi tiết đề thi học kì 1 môn toán lớp 6 năm 2020 - 2021 phòng GD-ĐT Thị xã Bình Minh với cách giải nhanh và chú ý quan trọng
Câu 1 (2 điểm): Thực hiện phép tính
a) 5.42 – 18:32
b) – 25 – (-15) + 24 – 12
Câu 2 (2 điểm): Tìm số tự nhiên x, biết
a) (x - 1).11 = 33
b) (1225 + 625) - 4x = 1000 – 150
Câu 3 (2 điểm): Học sinh của lớp 6A khi xếp hàng 2, hàng 4, hàng 5 thì vừa đủ hàng. Biết số học sinh của lớp trong khoảng từ 35 đến 60. Tính số học sinh của lớp.
Câu 4 (1 điểm): Trên tia Ox
a) Vẽ đoạn thẳng OA = 5cm
b) Vẽ đoạn thẳng AB = 3 cm
Câu 5 (2,5 điểm)
Cho đoạn thẳng AB = 4cm, C nằm giữa AB sao cho AC = 1cm. Gọi P và Q là trung điểm của AC và BC. Tính độ dài đoạn PQ.
Câu 6 (0,5 điểm):
So sánh hai số sau: 24000 và 42000
LỜI GIẢI CHI TIẾT
Câu 1:
a) 5.42 – 18:32 = 5.16 – 18 : 9 = 80 – 2 = 78.
b) – 25 – (-15) + 24 – 12 = - 25 + 15 + 24 -12
= -10 + 24 -12 = 14 -12 = 2
Câu 2:
a) (x - 1).11 = 33
x – 1 = 33 : 11
x – 1 =3
x = 3 + 1
x = 4
Vậy x = 4.
b) (1225 + 625) - 4x = 1000 – 150
1850 – 4x = 850
4x = 1850 – 850
4x = 1000
x = 1000: 4
x = 250
Vậy x = 250.
Câu 3:
Gọi số học sinh của lớp 6A là x (\(x \in \mathbb{N}\), 35 < x < 50)
Do khi xếp hàng 2, hàng 4, hàng 5 thì vừa đủ hàng nên:
\(x \vdots 2;\,\,x \vdots 4;\,\,x \vdots 5\,\, \Rightarrow x \in BCNN(2;\,4;\,5)\)
Ta có 2 = 2; 4 = 22; 5 = 5
\(BCNN(2;\,4;\,5) = {2^2}.5 = 20\)
\( \Rightarrow BC\left( {2;\,4;\,5} \right) = \left\{ {0;\,20;\,40;\,60;...} \right\}\)
Mà 35 < x < 50 nên x = 40.
Vậy số học sinh của lớp 6A là 40 học sinh.
Câu 4:
Trường hợp 1:
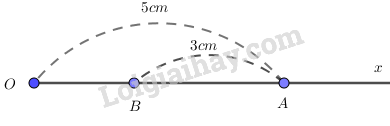
Trường hợp 2:
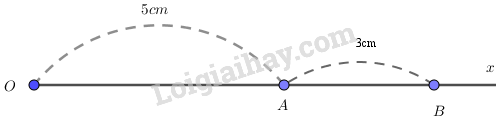
Câu 5:
Do C nằm giữa AB nên ta có:
AC + BC = AB
1 + BC = 4
BC = 4 – 1 = 3 cm
Do P và Q là trung điểm của AC và BC nên:
\(\begin{array}{l}AP = PC = \frac{{AC}}{2} = \frac{1}{2} = 0,5\\CQ = QB = \frac{{BC}}{2} = \frac{3}{2} = 1,5\end{array}\)
Do C nằm giữa A và B nên hai tia CA và CB đối nhau
Mà \(P \in AC;\,\,Q \in CB\)
Nên hai tia CP và CQ đối nhau => C nằm giữa P và Q
=> PQ = PC + CQ
=> PQ = 0,5 + 1,5 = 2(cm)
Vậy PQ = 2cm.
Câu 6:
Ta có:
\({2^{4000}} = {2^{1000.4}} = {\left( {{2^4}} \right)^{1000}} = {16^{1000}}\)
\({4^{2000}} = {4^{1000.2}} = {\left( {{4^2}} \right)^{1000}} = {16^{1000}}\)
Vậy \({2^{4000}} = {4^{2000}}\)
Loigiaihay.com
Bình luận
Chia sẻ
- Giải đề thi học kì 1 toán lớp 6 năm 2020 - 2021 quận 12
- Giải đề thi học kì 1 toán lớp 6 năm 2020 - 2021 phòng GD Thành phố Huế
- Giải đề thi học kì 1 toán lớp 6 năm 2020 - 2021 phòng GD TP Hải Dương
- Đề thi kì 1 môn toán lớp 6 năm 2019 - 2020 trường THCS Marie Curie
- Đề thi kì 1 môn toán lớp 6 năm 2019 - 2020 phòng GDĐT Tân Phú
>> Xem thêm
Tham Gia Group Dành Cho 2K13 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí
Các bài khác cùng chuyên mục
