Giải tuần 29: Tìm hai số khi biết hiệu và tỉ số của hai số đó. Luyện tập chung trang 40
Viết tiếp vào chỗ chấm cho thích hợp: Quãng đường từ nhà Mai đến trường học gồm hai đoạn đường. Viết số thích hợp vào chỗ chấm: Hai số có tổng là 64 và tỉ số là 3/5. Hai số đó là …….
Bài 1
Khoanh vào chữ đặt trước câu trả lời đúng:
Cho \(a = 7kg;\; b = 4kg\). Tỉ số của \(a\) và \(b\) là
A. \(\dfrac{7}{4}\) B. \(\dfrac{{7kg}}{{4kg}}\)
C. \(\dfrac{{4kg}}{{7kg}}\) D. \(\dfrac{4}{7}\)
Phương pháp giải:
Tỉ số của \(a\) và \(b\) là \(a:b\) hay \(\dfrac{a}{b}\) (\(b\) khác \(0\)).
Lời giải chi tiết:
Nếu \(a = 7kg;\; b = 4kg\) thì tỉ số của \(a\) và \(b\) là \(\dfrac{7}{4}\).
Chọn A.
Bài 2
Viết số thích hợp vào ô trống:
|
Hiệu của hai số |
18 |
40 |
16 |
|
Tỉ số của hai số |
\(\dfrac{5}{8}\) |
\(\dfrac{9}{5}\) |
\(\dfrac{3}{7}\) |
|
Số bé |
|
|
|
|
Số lớn |
|
|
|
Phương pháp giải:
Tính ra nháp theo các bước bên dưới, sau đó ghi kết quả vào bảng :
1. Vẽ sơ đồ: Biểu diễn số lớn và số bé theo tỉ số của hai số đó.
2. Tìm hiệu số phần bằng nhau.
3. Tìm giá trị của một phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé)
5. Tìm số lớn (lấy số bé cộng với hiệu của hai số ...)
Chú ý: Bước 3 và bước 4 có thể gộp thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
|
Hiệu của hai số |
18 |
40 |
16 |
|
Tỉ số của hai số |
\(\dfrac{5}{8}\) |
\(\dfrac{9}{5}\) |
\(\dfrac{3}{7}\) |
|
Số bé |
30 |
50 |
12 |
|
Số lớn |
48 |
90 |
28 |
Bài 3
Đoạn dây màu xanh dài hơn đoạn dây màu đỏ là 27m. Tỉ số độ dài của hai đoạn dây là \(\dfrac{2}{5}\). Tìm độ dài từng đoạn dây.
Phương pháp giải:
1. Vẽ sơ đồ: Coi độ dài đoạn dây màu đỏ (vai trò là số bé) gồm 2 phần bằng nhau thì độ dài đoạn dây màu xanh (vai trò là số lớn) gồm 5 phần như thế.
2. Tìm hiệu số phần bằng nhau.
3. Tìm giá trị của một phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé)
5. Tìm số lớn (lấy số bé cộng với hiệu của hai số ...)
Chú ý: Bước 3 và bước 4 có thể gộp thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Ta có sơ đồ:
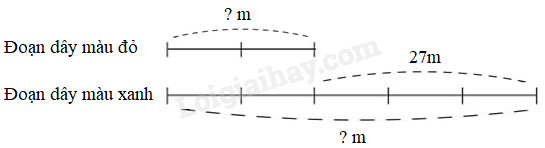
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 2 = 3 (phần)
Đoạn dây màu đỏ dài số mét là:
27 : 3 × 2 = 18 (m)
Đoạn dây màu xanh dài số mét là:
18 + 27 = 45 (m)
Đáp số: Đoạn dây màu đỏ: 18m;
Đoạn dây màu xanh: 45m.
Bài 4
Minh có nhiều hơn Hùng 27 viên bi. Số viên bi của Minh gấp 4 lần số viên bi của Hùng. Tìm số viên bi của Minh, số viên bi của Hùng.
Phương pháp giải:
1. Vẽ sơ đồ: Coi số viên bi của Hùng (vai trò là số bé) gồm 1 phần thì số viên bi của Minh (vai trò là số lớn) gồm 4 phần như thế.
2. Tìm hiệu số phần bằng nhau.
3. Tìm giá trị của một phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
5. Tìm số lớn (lấy số bé cộng với hiệu của hai số ...).
Chú ý: Bước 3 và bước 4 có thể gộp thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Ta có sơ đồ:
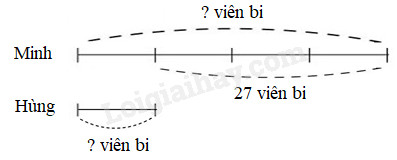
Theo sơ đồ, hiệu số phần bằng nhau là:
4 – 1 = 3 (phần)
Hùng có số viên bi là:
27 : 3 × 1 = 9 (viên bi)
Minh có số viên bi là:
9 × 4 = 36 (viên bi)
Đáp số: Minh: 36 viên bi ;
Hùng: 9 viên bi.
Bài 5
a) Nêu bài toán theo sơ đồ sau:
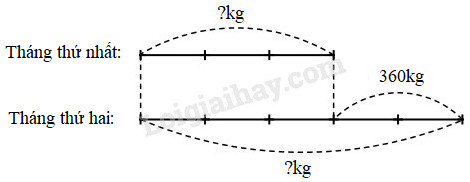
b) Trả lời: Tháng thứ nhất: ……. kg …….
Tháng thứ hai: ……. kg …….
Phương pháp giải:
- Quan sát sơ đồ tìm tỉ số và hiệu của hai số, sau đó nêu bài toán thích hợp.
- Giải bài toán:
1. Tìm hiệu số phần bằng nhau.
2. Tìm giá trị của một phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé) hoặc tìm số lớn trước.
5. Tìm số lớn (lấy số bé cộng với hiệu của hai số ...) hoặc tìm số bé (lấy số lớn trừ đi hiệu).
Chú ý: Bước 2 và bước 3 có thể gộp thành một bước.
Lời giải chi tiết:
a) Bài toán:
Nhà bác Hùng trồng cam trên một mảnh vườn hình chữ nhật. Tháng thứ hai thu hoạch được nhiều hơn tháng thứ nhất 360kg cam. Hỏi mỗi tháng bác Hùng thu hoạch được bao nhiêu ki-lô-gam cam, biết rằng tháng thứ nhất thu hoạch được số cam bằng \(\dfrac{3}{5}\) số cam của tháng thứ hai.
b)
Theo sơ đồ, hiệu số phần bằng nhau là:
5 – 3 = 2 (phần)
Tháng thứ nhất thu hoạch được số ki-lô-gam cam là:
360 : 2 × 3 = 540 (kg)
Tháng thứ hai thu hoạch được số ki-lô-gam cam là:
540 + 360 = 900 (kg)
Đáp số: Tháng thứ nhất: 540kg cam;
Tháng thứ hai: 900kg cam.
Bài 6
Viết tiếp vào chỗ chấm cho thích hợp:
Quãng đường từ nhà Mai đến trường học gồm hai đoạn đường (xem hình vẽ), đoạn đường từ nhà Mai đến chợ bằng \(\dfrac{3}{{10}}\) đoạn đường từ nhà Mai đến trường học. Biết đoạn đường từ chợ đến trường học là 1400m. Hỏi quãng đường từ nhà Mai đến trường học dài bao nhiêu mét?
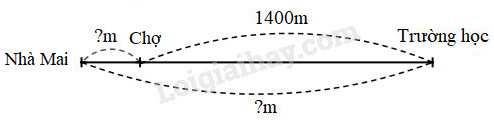
Phương pháp giải:
- Hiệu giữa quãng đường từ nhà Mai đến trường học và đoạn đường từ nhà Mai đến chợ chính là đoạn đường từ chợ đến trường học. Vậy hiệu giữa quãng đường từ nhà Mai đến trường học và đoạn đường từ nhà Mai đến chợ là 1400m.
- Vẽ sơ đồ : Coi đoạn đường từ nhà Mai đến chợ (vai trò là số bé) gồm 3 phần bằng nhau thì quãng đường từ nhà Mai đến trường học (vai trò là số lớn) gồm 10 phần như thế.
- Tìm hiệu số phần bằng nhau.
- Tìm giá trị của một phần bằng cách lấy hiệu hai số chia cho hiệu số phần bằng nhau.
- Tìm số lớn (lấy giá trị một phần nhân với số phần của số lớn).
Lưu ý : Hai bước cuối có thể làm gộp thành 1 bước.
Lời giải chi tiết:
Hiệu giữa quãng đường từ nhà Mai đến trường học và đoạn đường từ nhà Mai đến chợ chính là đoạn đường từ chợ đến trường học. Vậy hiệu giữa quãng đường từ nhà Mai đến trường học và đoạn đường từ nhà Mai đến chợ là 1400m.
Ta có sơ đồ:
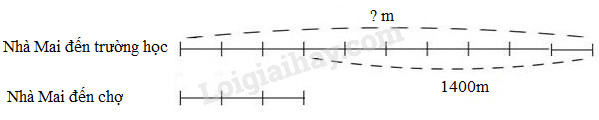
Theo sơ đồ, hiệu số phần bằng nhau là:
10 – 3 = 7 (phần)
Quãng đường từ nhà Mai đến trường học dài số mét là:
1400 : 7 × 10 = 2000 (m)
Đáp số: 2000m.
Bài 7
Viết số thích hợp vào chỗ chấm;
Hai số có tổng là 64 và tỉ số là \(\dfrac{3}{5}\). Hai số đó là …….
Phương pháp giải:
1. Vẽ sơ đồ: coi số bé gồm 3 phần bằng nhau thì số lớn gồm 5 phần như thế.
2. Tìm tổng số phần bằng nhau.
3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Ta có sơ đồ:
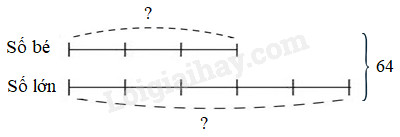
Theo sơ đồ, tổng số phần bằng nhau là:
\(3 + 5 = 8\) (phần)
Số bé là:
\(64:8 \times 3 = 24\)
Số lớn là:
\(64 - 24 = 40\)
Đáp số: Số lớn: \(40\);
Số bé: \(24\).
Bài 8
Giải bài toán:
Tổng lượng khách tham quan khu di tích tuần này và tuần trước là 360 lượt khách. Do thời tiết khôg thuận lợi nên số lượt khách tham quan tuần này giảm 2 lần so với tuần trước. Tính lượng khách tham quan từng tuần.
Phương pháp giải:
1. Vẽ sơ đồ: coi số khách tham quan tuần này (đóng vai trò số bé) gồm 1 phần thì số khách tham quan tuần trước (đóng vai trò số lớn) gồm 2 phần như thế.
2. Tìm tổng số phần bằng nhau.
3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Ta có sơ đồ:
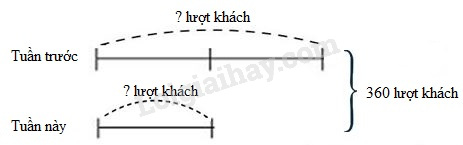
Theo sơ đồ, tổng số phần bằng nhau là:
1 + 2 = 3 (phần)
Lượng khách tham quan vườn bách thú tuần trước là:
360 : 3 × 2 = 240 (lượt khách)
Lượng khách tham quan vườn bách thú tuần trước là:
360 – 240 = 120 (lượt khách)
Đáp số: Tuần trước: 240 lượt khách;
Tuần này: 120 lượt khách.
Vui học
Viết tiếp vào chỗ chấm để được câu trả lời đúng:
Mẹ đi siêu thị mua có thịt, cá, rau và một số loại hoa quả. Biết số tiền mua hoa quả bằng \(\dfrac{1}{5}\) số tiền mua các loại thực phẩm khác. Mẹ đưa cho nhân viên ở quầy thu ngân 500 000 đồng và được trả lại 50 000 đồng. Hỏi mẹ mua hoa quả hết bao nhiêu tiền?

Phương pháp giải:
1. Vẽ sơ đồ: coi số tiền mua hoa quả (đóng vai trò số bé) gồm 1 phần thì số tiền mua các loại thực phẩm khác (đóng vai trò số lớn) gồm 5 phần như thế.
2. Tìm tổng số phần bằng nhau.
3. Tìm giá trị của 1 phần bằng cách lấy tổng hai số chia cho tổng số phần bằng nhau.
4. Tìm số bé (lấy giá trị một phần nhân với số phần của số bé).
5. Tìm số lớn (lấy tổng hai số trừ đi số bé, …).
Chú ý: Bước 3 và bước 4 có thể gộp lại thành một bước; có thể tìm số lớn trước rồi tìm số bé sau.
Lời giải chi tiết:
Số tiền nhân viên đã thu của mẹ là:
500 000 – 50 000 = 450 000 (đồng)
Ta có sơ đồ:

Theo sơ đồ, tổng số phần bằng nhau là:
1 + 5 = 6 (phần)
Giá trị 1 phần là:
450 000 : 6 = 75 000 (đồng)
Mẹ mua hoa quả hết số tiền là:
75 000 × 1 = 75 000 (đồng)
Đáp số: 75 000 đồng.
- Tuần 30: Luyện tập chung. Tỉ lệ bản đồ. Ứng dụng của tỉ lệ bản đồ. Thực hành trang 44
- Tuần 31: Thực hành (tiếp theo). Ôn tập về số tự nhiên và các phép tính với số tự nhiên (trang 47)
- Tuần 32: Ôn tập về phép tính với số tự nhiên (tiếp theo). Ôn tập về biểu đồ. Ôn tập về phân số và các phép tính với phân số trang 50
- Tuần 33: Ôn tâp về các phép tính với phân số (tiếp theo). Ôn tập về đại lượng (trang 53)
- Tuần 34: Ôn tập: Đại lượng, hình học, tìm số trung bình cộng, tìm hai số khi biết tổng và hiệu của hai số đó (trang 56)
>> Xem thêm
Các bài khác cùng chuyên mục
- Tuần 35: Ôn tập về tìm hai số khi biết tổng hoặc hiệu và tỉ số của hai số đó. Luyện tập chung (trang 60)
- Tuần 34: Ôn tập: Đại lượng, hình học, tìm số trung bình cộng, tìm hai số khi biết tổng và hiệu của hai số đó (trang 56)
- Giải tuần 3: Triệu và lớp triệu (tiếp theo). Dãy số tự nhiên. viết số tự nhiên trong hệ thập phân - Cùng em học Toán 4
- Giải tuần 1: Ôn tập các số đến 100 000. Biểu thức có chứa một chữ - Cùng em học Toán 4
- Giải tuần 2. Các số có sáu chữ số. Hàng và lớp. So sánh các số có nhiều chữ số. Triệu và lớp triệu
- Tuần 35: Ôn tập về tìm hai số khi biết tổng hoặc hiệu và tỉ số của hai số đó. Luyện tập chung (trang 60)
- Tuần 34: Ôn tập: Đại lượng, hình học, tìm số trung bình cộng, tìm hai số khi biết tổng và hiệu của hai số đó (trang 56)
- Giải tuần 3: Triệu và lớp triệu (tiếp theo). Dãy số tự nhiên. viết số tự nhiên trong hệ thập phân - Cùng em học Toán 4
- Giải tuần 1: Ôn tập các số đến 100 000. Biểu thức có chứa một chữ - Cùng em học Toán 4
- Giải tuần 2. Các số có sáu chữ số. Hàng và lớp. So sánh các số có nhiều chữ số. Triệu và lớp triệu












Danh sách bình luận