Giải vth Toán 9, soạn vở thực hành Toán 9 KNTT

Bài 1. Khái niệm phương trình và hệ hai phương trình bậ..

Giải câu hỏi trắc nghiệm trang 5, 6 vở thực hành Toán 9

Phương trình nào sau đây là phương trình bậc nhất hai ẩn? A. ({x^2} - y = 2). B. (2x + y = 0). C. (0x - 0y = - 2). D. ({x^2} + {y^2} = 5).

Tổng hợp đề thi giữa kì 1 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - Khoa học tự nhiên

Lựa chọn câu để xem lời giải nhanh hơn

Chọn phương án đúng trong mỗi câu sau:

Câu 1

Trả lời Câu 1 trang 5 Vở thực hành Toán 9

Phương trình nào sau đây là phương trình bậc nhất hai ẩn?

A. \({x^2} - y = 2\).

B. \(2x + y = 0\).

C. \(0x - 0y = - 2\).

D. \({x^2} + {y^2} = 5\).

Phương pháp giải:

Phương trình bậc nhất hai ẩn x và y là hệ thức dạng \(ax + by = c\), trong đó a, b, c, là các số đã biết (\(a \ne 0\) hoặc \(b \ne 0\)).

Lời giải chi tiết:

Phương trình \(2x + y = 0\) là phương trình bậc nhất hai ẩn.

Chọn B

Câu 2

Trả lời Câu 2 trang 6 Vở thực hành Toán 9

Nghiệm (tổng quát) của phương trình \( - 2x - 3y = 6\) là

A. \(\left( {x;\frac{2}{3}x + 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

B. \(\left( {\frac{3}{2}y + 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

C. \(\left( {\frac{3}{2}y - 3;y} \right)\) với \(y \in \mathbb{R}\) tùy ý.

D. \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Phương pháp giải:

Từ phương trình đầu bài cho, ta tính x theo y hoặc y theo x, từ đó kết luận được nghiệm tổng quát của phương trình.

Lời giải chi tiết:

Ta có: \( - 2x - 3y = 6\), suy ra \(y = \frac{{ - 2}}{3}x - 2\).

Do đó, nghiệm tổng quát của phương trình \( - 2x - 3y = 6\) là \(\left( {x;\frac{{ - 2}}{3}x - 2} \right)\) với \(x \in \mathbb{R}\) tùy ý.

Chọn D

Câu 3

Trả lời Câu 3 trang 6 Vở thực hành Toán 9

Cho hai phương trình \( - 3x + y = - 7\;\left( 1 \right)\) và \(x - 2y = 4\;\left( 2 \right)\). Cặp số nào sau đây là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?

A. \(\left( {0; - 7} \right)\).

B. \(\left( {6;1} \right)\).

C. \(\left( {2; - 1} \right)\).

D. \(\left( { - 1; - 10} \right)\).

Phương pháp giải:

Mỗi cặp số \(\left( {{x_0};{y_0}} \right)\) được gọi là một nghiệm của hệ \(\left\{ \begin{array}{l}ax + by = c\\a'x + b'y = c'\end{array} \right.\) (*) nếu nó đồng thời là nghiệm của cả hai phương trình của hệ (*).

Lời giải chi tiết:

Với \(x = 2;y = - 1\) ta có:

\( - 3.2 + \left( { - 1} \right) = - 7\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (1).

\(2 - 2\left( { - 1} \right) = 4\) nên \(\left( {2; - 1} \right)\) là nghiệm của phương trình (2).

Do đó, \(\left( {2; - 1} \right)\) là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2).

Chọn C

Câu 4

Trả lời Câu 4 trang 6 Vở thực hành Toán 9

Hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn nào sau đây? trong đầu bài nó ghi là pt 1 ẩn, nhưng đúng là pt hai ẩn nên t sửa đề cho đúng luôn nhé

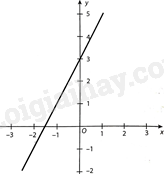
A. \(2x - y = - 3\).

B. \(2x + y = 3\).

C. \(3x + y = 3\).

D. \(3x - y = 0\).

Phương pháp giải:

Trong mặt phẳng tọa độ, tập hợp các điểm có tọa độ (x; y) thỏa mãn phương trình bậc nhất hai ẩn \(ax + by = c\) là một đường thẳng. Đường thẳng đó gọi là đường thẳng \(ax + by = c\).

Lời giải chi tiết:

Ta thấy, các điểm (0; 3) và \(\left( {\frac{{ - 3}}{2};0} \right)\) thuộc đường thẳng cần tìm.

Do đó, đường thẳng cần tìm là: \(2x - y = - 3\).

Vậy hình vẽ bên biểu diễn tập nghiệm của phương trình bậc nhất hai ẩn \(2x - y = - 3\).

Chọn A

👉

Giải bài nhanh với AI Hay:

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 1 trang 6 vở thực hành Toán 9
Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Vì sao? a) (5x - 8y = 0); b) (4x + 0y = - 2); c) (0x + 0y = 1); d) (0x - 3y = 9).
Giải bài 2 trang 6 vở thực hành Toán 9
a) Tìm giá trị thích hợp thay cho dấu “?” trong bảng sau rồi cho biết 6 nghiệm của phương trình (2x - y = 1): b) Viết nghiệm tổng quát của phương trình đã cho.
Giải bài 3 trang 7 vở thực hành Toán 9
Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau: a) (2x - y = 3); b) (0x + 2y = - 4); c) (3x + 0y = 5).
Giải bài 4 trang 8 vở thực hành Toán 9
Cho hệ phương trình (left{ begin{array}{l}2x = - 65x + 4y = 1end{array} right.) a) Hệ phương trình trên có là một hệ phương trình bậc nhất hai ẩn không? Vì sao? b) Cặp số (left( { - 3;4} right)) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?
Giải bài 5 trang 9 vở thực hành Toán 9
Cho hệ phương trình bậc nhất hai ẩn (left{ begin{array}{l}3x + 2y = 1\x - 3y = - 7end{array} right.). Chứng tỏ rằng hệ phương trình đã cho có một nghiệm là (left( { - 1;2} right)).
Giải bài 6 trang 9 vở thực hành Toán 9
Cho các cặp số (-2; 1), (0; 2), (1; 0), (1,5; 3), (4; -3) và hai phương trình (5x + 4y = 8), (1) (3x + 5y = - 3) (2) Trong các cặp số đã cho: a) Những cặp số nào là nghiệm của phương trình (1)? b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)? c) Vẽ hai đường thẳng (5x + 4y = 8) và (3x + 5y = - 3) trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.
Giải bài 7 trang 9 vở thực hành Toán 9
Cho phương trình bậc nhất hai ẩn (3x + 2my = - 5). a) Xác định m để cặp số (-1; 2) là một nghiệm của phương trình đã cho. b) Viết công thức nghiệm tổng quát của phương trình với m tìm được ở câu a.