Bài V.9, V.10, V.11, V.12, V.13 trang 76 SBT Vật lí 10

V.9.

Một bình chứa một lượng khí ở nhiệt độ 27°C và áp suất 40 atm. Nếu giảm nhiệt độ xuống tới 12°C và để một nửa lượng khí thoát ra ngoài thì áp suất khí còn lại trong bình sẽ bằng bao nhiêu ?

Phương pháp giải:

Áp dụng phương trình trạng thái của khí lí tưởng

\(\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\)

Lời giải chi tiết:

Xét lượng khí còn lại trong bình

Trạng thái 1: V₁ = V/2; T₁ = 27 + 273 = 300 K; p₁ = 40 atm.

Trạng thái 2: V₂ = V; T₂ = 12 + 273 = 285 K; p₂ = ? atm,

Từ  \({{{p_1}{V_1}} \over {{T_1}}} = {{{p_2}{V_2}} \over {{T_2}}} = > {p_2} = {{{p_1}{V_1}{T_2}} \over {{T_1}}} = 19(atm)\)

V.10.

Người ta dùng một bơm tay có ống bơm dài 50 cm và đường kính trong 4 cm để bơm không khí vào một túi cao su sao cho túi phồng lên, có thể tích là 6,28 lít và áp suất không khí trong túi là 4 atm. Biết áp suất khí quyển là 1 atm và coi nhiệt độ của không khí được bơm vào túi không đổi.

Phương pháp giải:

Áp dụng định luật Bôi lơ ma ri ốt \({p_1}{V_1} = {p_2}{V_2}\)

Lời giải chi tiết:

Mỗi lần bơm, người ta đưa được vào trong túi cao su một lượng không khí có thể tích \({V_0} = {{\pi {d^2}l} \over 4}\) , áp suất p₀ = 1 atm.

Khi được bơm vào túi ở áp suất p = 4 atm, lượng không khí này có thể tích V. Vì nhiệt độ không đổi nên:

pV = p₀V₀ => V = 0,157.10^-3 m³

Số lần bơm:  \(n = {{6,{{28.10}^{ - 3}}} \over {0,{{157.10}^{ - 3}}}} = 40\)

V.11.

Một bơm xe đạp hình trụ có đường kính trong là 3 cm. Người ta dùng ngón tay bịt kín đầu vòi bơm và ấn pit-tông từ từ để nén không khí trong bơm sao cho nhiệt độ không thay đổi. Tính lực tác dụng lên pit-tông khi thể tích của không khí trong bơm giảm đi 4 lần. Lấy áp suất khí quyển là p_a= 10⁵ Pa.

Phương pháp giải:

Áp dụng công thức:

+ Áp suất \(p = \dfrac{F}{S}\)

+ Định luật Bôi lơ ma ri ốt \({p_1}{V_1} = {p_2}{V_2}\)

+ Diện tích hình tròn \(S = \pi {r^2}\)

Lời giải chi tiết:

Trạng thái đầu: p₁ = p_a ; V₁ = V; T₁.

Trong đó p_a là áp suất khí quyển.

Trạng thái cuối: p₂ = p_a + p = p_a + F/S ; V₂  = V/4 ; T₂ = T₁.

Trong đó p là áp suất gây ra bởi lực F của tay; S là diện tích của pit-tông:  \(S = {{\pi {d^2}} \over 4}\)

Dùng định luật Bôi-lơ – Ma-ri-ốt, dễ dàng tính được:

\(F = 3{p_a}.{{\pi {d^2}} \over 4} \approx 212(N)\)

V.12.

Trong một bình kín dung tích 20 lít có chứa 4,4 kg khí cacbonic ở nhiệt độ 27°C. Tính áp suất của khí trong bình. Biết thể tích của một mol khí ở điều kiện chuẩn là V₀= 22,4 lít.

Phương pháp giải:

Áp dụng công thức:

+ Số mol \(n = \dfrac{m}{M}\)

+ Phương trình trạng thái của khí lí tưởng \(\dfrac{{{p_1}{V_1}}}{{{T_1}}} = \dfrac{{{p_2}{V_2}}}{{{T_2}}}\)

Lời giải chi tiết:

Gọi n là số mol khí cacbonic chứa trong bình: \(n = {M \over \mu }\) , trong đó M là khối lượng khí cacbonic có trong bình, µ là khối lượng mol của khí cacbonic.

Ta có n = 100 mol

Nếu gọi V₀ là thể tích của lượng khí cacbonic ở điều kiện chuẩn (p₀ = 1,013.10⁵ Pa; T₀ = 273 K) thì V₀ = nv₀.

Áp dụng phương trình trạng thái của khí lí tưởng cho lượng khí cacbonic:

\({{pV} \over T} = {{{p_0}{V_0}} \over {{T_0}}} = {{{p_0}n{v_0}} \over {{T_0}}} = > p = {{{p_0}n{v_0}T} \over {V.{T_0}}} \approx {125.10^5}(Pa)\)

V.13.

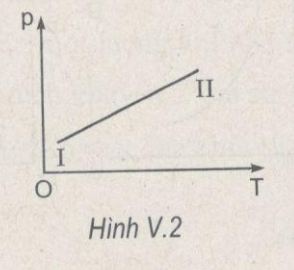
Một chất khí chuyển từ trạng thái I sang trạng thái II (H.V.2). Khi đó các thông số trạng thái của chất khí đã thay đổi như thế nào, nếu khối lượng khí không đổi ?

Phương pháp giải:

+ Sử dụng lí thuyết về đồ thị đường đẳng tích 

+ Áp dụng định luật Bôi lơ ma ri ốt \({p_1}{V_1} = {p_2}{V_2}\)

Lời giải chi tiết:

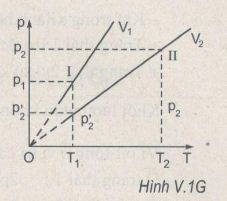
Trên hình V.1G ta thấy, khi chất khí chuyển từ trạng thái I sang trạng thái II, thì nhiệt độ T và áp suất p đều tăng

Vẽ các đường đẳng tích V₁ (qua I) và V₂ (qua II). Với các nhiệt độ T₁ thì các thể tích này ứng với các áp suất p₁ và p’₂. Như vậy, ứng với nhiệt độ T₁, ta có:

p₁V₁ = p’₂V₂

Từ đồ thị ta thấy p₁ > p’₂, do đó suy ra V₁ < V₂.

Tóm lại ta có: V₁ < V₂; p₁ < p₂ ; T₁ < T₂

Loigiaihay.com