Giải bài tập 5.44 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng A. \(\frac{1}{2}R\). B. R. C. 2R. D. \(R\sqrt 2 \).
Đề bài
Cho MA và MB là hai tiếp tuyến của đường tròn (O; R) (A, B là hai tiếp điểm) sao cho \(\Delta \)MAB là tam giác đều. Khoảng cách OM bằng
A. \(\frac{1}{2}R\).
B. R.
C. 2R.
D. \(R\sqrt 2 \).
Phương pháp giải - Xem chi tiết
+ Chứng minh \(\widehat {AMB} = {60^o}\).
+ Chứng minh MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB}\).
+ Chứng minh tam giác AOM vuông tại M nên \(AO = MO.\sin AMO\), từ đó tính được MO.
Lời giải chi tiết
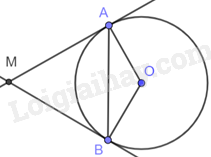
Vì tam giác MAB đều nên \(\widehat {AMB} = {60^o}\).
Vì MA và MB là tiếp tuyến của (O) nên MO là tia phân giác \(\widehat {AMB}\), nên \(\widehat {AMO} = \frac{1}{2}\widehat {AMB} = \frac{1}{2}{.60^o} = {30^o}\)
Vì MA là tiếp tuyến của (O) nên \(MA \bot AO\). Do đó, tam giác MAO vuông tại A.
Suy ra, \(AO = MO.\sin AMO\) nên
\(MO = \frac{{AO}}{{\sin AMO}} = \frac{R}{{\sin {{30}^o}}} = 2R\).
Chọn C
- Giải bài tập 5.45 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.46 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.47 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.48 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
- Giải bài tập 5.43 trang 129 SGK Toán 9 tập 1 - Cùng khám phá
>> Xem thêm
Các bài khác cùng chuyên mục
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá
- Lý thuyết Cách tính xác suất của biến cố trong một số mô hình đơn giản Toán 9 Cùng khám phá
- Lý thuyết Phép thử ngẫu nhiên. Không gian mẫu Toán 9 Cùng khám phá
- Lý thuyết Tần số ghép nhóm, tần số tương đối ghép nhóm Toán 9 Cùng khám phá
- Lý thuyết Tần số tương đối Toán 9 Cùng khám phá
- Lý thuyết Tần số Toán 9 Cùng khám phá













Danh sách bình luận