Toán 12 Cùng khám phá | Giải toán lớp 12 Cùng khám phá Bài tập cuối chương 5 - Toán 12 Cùng khám phá

Giải bài tập 5.43 trang 86 SGK Toán 12 tập 2 - Cùng khám phá


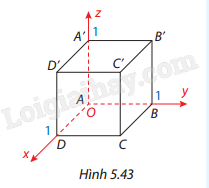
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, với A(0; 0; 0), D(1; 0; 0), B(0; 1; 0), A’(0; 0; 1). a) Chứng minh \(A'C \bot (AB'D')\). b) Chứng minh \((AB'D')//(C'BD)\)và tính khoảng cách giữa hai mặt phẳng \((AB'D')\) và \((C'BD)\). c) Tính côsin của góc giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\).

GÓP Ý HAY - NHẬN NGAY QUÀ CHẤT

Gửi góp ý cho Loigiaihay.com và nhận về những phần quà hấp dẫn

Đề bài

Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng 1, với A(0; 0; 0), D(1; 0; 0), B(0; 1; 0), A’(0; 0; 1).

a) Chứng minh \(A'C \bot (AB'D')\).

b) Chứng minh \((AB'D')//(C'BD)\)và tính khoảng cách giữa hai mặt phẳng \((AB'D')\) và \((C'BD)\).

c) Tính côsin của góc giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\).

Phương pháp giải - Xem chi tiết

a) Chứng minh đường thẳng vuông góc với mặt phẳng:

- Tìm véc-tơ pháp tuyến của mặt phẳng bằng tích có hướng của hai véc-tơ trong mặt phẳng.

- Kiểm tra tích vô hướng giữa véc-tơ chỉ phương của đường thẳng và véc-tơ pháp tuyến của mặt phẳng. Nếu tích vô hướng bằng 0, đường thẳng vuông góc với mặt phẳng.

b) Chứng minh hai mặt phẳng song song và tính khoảng cách:

- Tìm véc-tơ pháp tuyến của từng mặt phẳng. Nếu hai véc-tơ pháp tuyến cùng phương, hai mặt phẳng song song.

- Tính khoảng cách giữa hai mặt phẳng song song bằng công thức khoảng cách từ điểm đến mặt phẳng.

c) Tính góc giữa hai mặt phẳng:

- Tìm véc-tơ pháp tuyến của mỗi mặt phẳng.

- Dùng công thức  để tính góc giữa hai mặt phẳng.

Lời giải chi tiết

Các đỉnh còn lại có toạ độ là: \(C(1;1;0)\), \(B'(0;1;1)\), \(C'(1;1;1)\), \(D'(1;0;1)\)

a) Chứng minh \(A'C \bot (AB'D')\)

Véc-tơ pháp tuyến của \((AB'D')\):

\(\overrightarrow {AB'}  = (0;1;1),\quad \overrightarrow {AD'}  = (1;0;1)\)

\({\vec n_{(AB'D')}} = \overrightarrow {AB'}  \times \overrightarrow {AD'}  = (1;1; - 1)\)

Mà ta có: \(\overrightarrow {A'C}  = (1;1; - 1)\)trùng với vec-tơ pháp tuyến của \((AB'D')\)

Vậy \(A'C \bot (AB'D')\).

b) Chứng minh \((AB'D')\parallel (C'BD)\) và tính khoảng cách

Véc-tơ pháp tuyến của \((C'BD)\):

\(\overrightarrow {C'B}  = ( - 1;0; - 1),\quad \overrightarrow {C'D}  = (0; - 1; - 1)\)

\({\vec n_{(C'BD)}} = \overrightarrow {C'B}  \times \overrightarrow {C'D}  = ( - 1; - 1;1)\)

Hai véc-tơ pháp tuyến \({\vec n_{(AB'D')}}\) và \({\vec n_{(C'BD)}}\) cùng phương nên \((AB'D')\parallel (C'BD)\).

* Khoảng cách giữa hai mặt phẳng:

Chọn điểm \(A(0,0,0)\) thuộc \((AB'D')\).

Phương trình \((C'BD)\): \(1.(x - 0) - 1.(y - 1) - (z - 0) = 0 \Leftrightarrow x - y - z + 1 = 0\).

\(d = \frac{{|0 \cdot 1 - 0 \cdot 1 - 0 \cdot ( - 1) + 1|}}{{\sqrt {{{( - 1)}^2} + {{( - 1)}^2} + {1^2}} }} = \frac{1}{{\sqrt 3 }}\)

c) Tính \(\cos \theta \) giữa hai mặt phẳng \((DA'C')\) và \((ABB'A')\)

- Véc-tơ pháp tuyến của \((DA'C')\):

\(\overrightarrow {DA'}  = ( - 1;0;1),\quad \overrightarrow {DC'}  = (0;1;1)\)

\({\vec n_{(DA'C')}} = \overrightarrow {DA'}  \times \overrightarrow {DC'}  = ( - 1;1; - 1)\)

Véc-tơ pháp tuyến của \((ABB'A')\):

\(\overrightarrow {AB}  = (0,1,0),\quad \overrightarrow {AA'}  = (0,0,1)\)

\({\vec n_{(ABB'A')}} = \overrightarrow {AB}  \times \overrightarrow {AA'}  = (1,0,0)\)

Tính \(\cos \theta \):

\({\vec n_{(DA'C')}} \cdot {\vec n_{(ABB'A')}} = ( - 1;1; - 1) \cdot (1;0;0) =  - 1\)

\(\cos \theta  = \frac{{| - 1|}}{{\sqrt 3  \cdot 1}} = \frac{1}{{\sqrt 3 }}\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo
  • Giải bài tập 5.44 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

    Cho hình chóp S.ABCD với ABCD là hình chữ nhật có A(0; 0; 0), B(1; 0; 0), D(0; 3; 0), S(0; 0; 2). a) Tính khoảng cách từ A đến mặt phẳng (SBD). b) Tính sin của góc giữa đường thẳng SD và mặt phẳng (SAB). c) Tính côsin của góc giữa hai mặt phẳng (SBC) và (SCD).

  • Giải bài tập 5.45 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

    Cho hai điểm A(1; 3; 0) và B(5; 1; −2). Mặt phẳng trung trực của đoạn thẳng AB có phương trình là

  • Giải bài tập 5.46 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

    Cho mặt phẳng (left( alpha right)) đi qua điểm M(0; 0; −1), có cặp vectơ chỉ phương là (vec a = left( { - 1;2; - 3} right)) và (vec b = left( {3;0;5} right)). Phương trình của mặt phẳng (left( alpha right)) là

  • Giải bài tập 5.47 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

    Cho ba điểm A(3; 0; 1), B(0; 2; 1), C(1; 0; 0). Phương trình của mặt phẳng (ABC) là A. \(2x - 3y - 4z + 2 = 0\) B. \(2x + 3y - 4z - 2 = 0\) C. \(4x + 6y - 8z + 2 = 0\) D. \(2x - 3y - 4z + 1 = 0\)

  • Giải bài tập 5.48 trang 86 SGK Toán 12 tập 2 - Cùng khám phá

    Cho điểm M(3; −1; −2) và mặt phẳng \((\alpha )\): 3x − y + 2z + 4 = 0. Mặt phẳng đi qua M và song song với \((\alpha )\)có phương trình là A. \(3x + y - 2z - 14 = 0\) B. \(3x - y + 2z + 6 = 0\) C. \(3x - y + 2z - 6 = 0\) D. \(3x - y - 2z + 6 = 0\)

>> Xem thêm

Báo lỗi - Góp ý

Group 2K8 ôn Thi ĐGNL & ĐGTD Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Hãy viết chi tiết giúp Loigiaihay.com

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Vấn đề em gặp phải là gì ?

Hãy viết chi tiết giúp Loigiaihay.com

Cảm ơn bạn đã sử dụng Loigiaihay.com. Đội ngũ giáo viên cần cải thiện điều gì để bạn cho bài viết này 5* vậy?

Vui lòng để lại thông tin để ad có thể liên hệ với em nhé!

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store