Giải bài tập 5.22 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức

Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).

Đề bài

Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Ta có: OA là tiếp tuyến của đường tròn (M; MA) do OA \( \bot \) MA tại A.

Xét cặp tam giác OAM và tam giác OBM, từ đó suy ra MA = MB và OB \( \bot \) MB. Hay OB là tiếp tuyến của đường tròn (M; MA).

Lời giải chi tiết

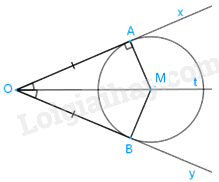
Ta có: OA là tiếp tuyến của đường tròn (M; MA) do OA \( \bot \) MA tại A.

Xét tam giác OAM và tam giác OBM có:

OM chung

\(\widehat {{\rm{AOM}}} = \widehat {{\rm{BOM}}}\) (do OM là tia phân giác của góc \(\widehat {{\rm{AOB}}}\))

OA = OB

Vậy \(\Delta {\rm{OAM}} = \Delta {\rm{OBM}}\) (c.g.c)

Suy ra: MA = MB (hai cạnh tương ứng)

\(\widehat {{\rm{OAM}}} = \widehat {{\rm{OBM}}} = 90^\circ \) (hai góc tương ứng) hay OB \( \bot \) MB

Do đó OA là tiếp tuyến của đường tròn (M; MA)

Vậy OA và OB là hai tiếp tuyến cắt nhau của (O).

Bình luận

Chia sẻ

Bình chọn:

3.8 trên 5 phiếu

Bài tiếp theo

Giải bài tập 5.23 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Cho SA và SB là hai tiếp tuyến cắt nhau của đường tròn (O) (A và B là hai tiếp điểm). Gọi M là một điểm tùy ý trên cung nhỏ AB. Tiếp tuyến của (O) tại M cắt SA tại E và cắt SB tại F. a) Chứng minh rằng chu vi của tam giác SEF bằng SA + SB. b) Giả sử M là giao điểm của đoạn SO với đường tròn (O). Chứng minh rằng SE = SF.
Giải bài tập 5.21 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).
Giải bài tập 5.20 trang 103 SGK Toán 9 tập 1 - Kết nối tri thức
Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b.
Giải mục 3 trang 101, 102, 103 SGK Toán 9 tập 1 - Kết nối tri thức
Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau: - Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B; - Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).
Giải mục 2 trang 100 SGK Toán 9 tập 1 - Kết nối tri thức
Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H. a) Xác định khoảng cách từ O đến đường thẳng a. b) Nếu vẽ đường tròn (O; OH) thì đường tròn này và đường thẳng a có vị trí tương đối như thế nào?
Giải mục 1 trang 99, 100 SGK Toán 9 tập 1 - Kết nối tri thức
Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?
Lý thuyết Vị trí tương đối của đường thẳng và đường tròn Toán 9 Kết nối tri thức
1. Vị trí tương đối của đường thẳng và đường tròn