Giải bài tập 4.1 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức

Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết: a) AB = 8 cm, BC = 17 cm; b) AC = 0,9 cm, AB = 1,2 cm.

Đề bài

Cho tam giác ABC vuông tại A. Tính các tỉ số lượng giác sin, cosin, tang, cotang của các góc nhọn B và C khi biết:

a) AB = 8 cm, BC = 17 cm;

b) AC = 0,9 cm, AB = 1,2 cm.

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sử dụng các tỉ số lượng giác để giải.

Lời giải chi tiết

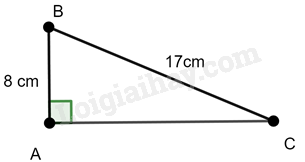
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)

Thay số ta có \({17^2} = {8^2} + A{C^2}\) hay \(A{C^2} = {17^2} - {8^2} = 225\) suy ra \(AC = 15\) cm (vì \(AC > 0\))

Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{15}}{{17}}\)

\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{8}{{17}}\)

\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{15}}{8}\)

\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{8}{{15}}\)

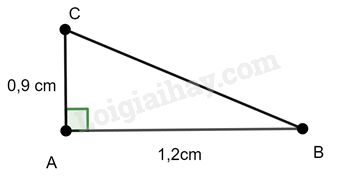
Tam giác ABC vuông tại A nên ta có: \(B{C^2} = A{B^2} + A{C^2}\) (Định lý Pythagore)

Thay số ta có \(B{C^2} = 1,{2^2} + 0,{9^2} = 2,25\) hay \(CB = \sqrt {2,25} = 1,5\) cm (vì \(BC > 0\))

Ta có: \(\sin \widehat B = \cos \widehat C = \frac{{AC}}{{BC}} = \frac{{0,9}}{{1,5}} = \frac{3}{5}\)

\(\cos \widehat B = \sin \widehat C = \frac{{AB}}{{BC}} = \frac{{1,2}}{{1,5}} = \frac{4}{5}\)

\(\tan \widehat B = \cot \widehat C = \frac{{AC}}{{AB}} = \frac{{0,9}}{{1,2}} = \frac{3}{4}\)

\(\cot \widehat B = \tan \widehat C = \frac{{AB}}{{AC}} = \frac{{1,2}}{{0,9}} = \frac{4}{3}\)

Bình luận

Chia sẻ

Bình chọn:

4.1 trên 12 phiếu

Bài tiếp theo

Giải bài tập 4.2 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác vuông có 1 góc nhọn ({60^0}) và cạnh kề với góc ({60^0}) bằng 3 cm. Hãy tính cạnh đối của góc này.
Giải bài tập 4.3 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác vuông có một góc nhọn bằng ({30^0}) và cạnh đối với góc này bằng 5 cm. Tính độ dài cạnh huyền của tam giác.
Giải bài tập 4.4 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
Cho hình chữ nhật có chiều dài và chiều rộng lần lượt là 3 và (sqrt 3 .) Tính góc giữa đường chéo và cạnh ngắn hơn của hình chữ nhật (sử dụng bảng giá trị lượng giác trang 69) .
Giải bài tập 4.5 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
a) Viết các tỉ số lượng giác sau thành tỉ số lượng giác của các góc nhỏ hơn ({45^0}:) (sin {55^0};cos {62^0};tan {57^0};cot {64^0}) b) Tính (frac{{tan {{25}^0}}}{{cot {{65}^0}}},tan {34^0} - cot {56^0}.)
Giải bài tập 4.6 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
Dùng MTCT, tính (làm tròn đến chữ số thập phân thứ ba) : a) (sin {40^0}12';) b) (cos {52^0}54';) c) (tan {63^0}36';) d) (cot {25^0}18'.)
Giải bài tập 4.7 trang 73 SGK Toán 9 tập 1 - Kết nối tri thức
Dùng MTCT, tìm số đo của góc nhọn x (làm tròn đến phút) , biết rằng: a) (sin x = 0,2368;) b) (cos x = 0,6224;) c) (tan x = 1,236;) d) (cot x = 2,154.)
Giải mục 3 trang 71, 72 SGK Toán 9 tập 1 - Kết nối tri thức
Sử dụng MTCT tính các ti số lượng giác và làm tròn kết quả đến chữ số thập phân thứ ba: a) (sin {40^0}54';) b) (cos {52^0}15';) c) (tan {69^0}36') d) (cot {25^0}18')
Giải mục 2 trang 70 SGK Toán 9 tập 1 - Kết nối tri thức
Cho tam giác ABC vuông tại C, có (widehat A = alpha ,widehat B = beta ) (H.4.9) . Hãy viết các tỉ số lượng giác của góc (alpha ,beta ) theo độ dài các cạnh của tam giác ABC. Trong các tỉ số đó, cho biết các cặp tỉ số bằng nhau.
Giải mục 1 trang 67, 68, 69 SGK Toán 9 tập 1 - Kết nối tri thức
Xét góc C của tam giác ABC vuông tại A (H.4.3) . Hãy chỉ ra cạnh đối và cạnh kề của góc C.
Lý thuyết Tỉ số lượng giác của góc nhọn Toán 9 Kết nối tri thức
1. Khái niệm tỉ số lượng giác của một góc nhọn