 Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
Giải vth Toán 7, soạn vở thực hành Toán 7 KNTT
 Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Bài 16. Tam giác cân. Đường trung trực của đoạn thẳng t..
Giải bài 7 trang 75 vở thực hành Toán 7
Bài 7. Cho tam giác ABC và điểm D nằm trên cạnh BC sao cho AD vuông góc với BC và AD là phân giác góc BAC. Chứng minh rằng \(\Delta ABC\)cân tại A.
Đề bài
Bài 7. Cho tam giác ABC và điểm D nằm trên cạnh BC sao cho AD vuông góc với BC và AD là phân giác góc BAC. Chứng minh rằng \(\Delta ABC\)cân tại A.
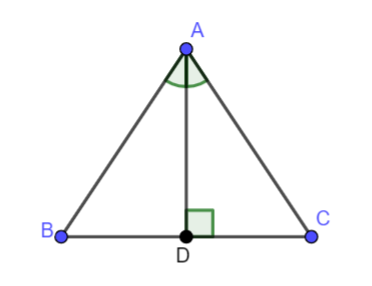
Phương pháp giải - Xem chi tiết
Tam giác cân là tam giác có hai cạnh bằng nhau.
Lời giải chi tiết
|
GT |
\(\Delta ABC\), \(D \in BC,AD \bot BC,\widehat {BAD} = \widehat {CAD}\) |
|
KL |
\(\Delta ABC\)cân tại A. |
Hai tam giác ADB và ADC cùng vuông tại D và có:
AD là cạnh chung
\(\widehat {BAD} = \widehat {CAD}\)(theo giả thiết)
Vậy \(\Delta ADB = \Delta ADC\)(cạnh góc vuông – góc nhọn).
Do đó AB = AC hay \(\Delta ABC\)cân tại A.
- Giải bài 8 trang 75 vở thực hành Toán 7
- Giải bài 6 (4.28) trang 75 vở thực hành Toán 7
- Giải bài 5 (4.27) trang 74 vở thực hành Toán 7
- Giải bài 4 (4.26) trang 74 vở thực hành Toán 7
- Giải bài 3 (4.25) trang 73 vở thực hành Toán 7
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 7 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục











