Giải bài 9 trang 108, 109, 110 vở thực hành Toán 7 tập 2

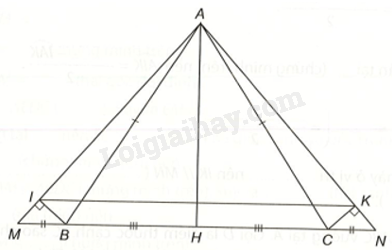
Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC. a) Chứng minh (AH bot BC). b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho (BM = CN). Chứng minh rằng (Delta ABM = Delta ACN). c) Gọi I là điểm trên AM, K là điểm trên AN sao cho (BI bot AM;CK bot AN). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN.

Đề bài

Cho tam giác ABC cân tại đỉnh A. Gọi H là trung điểm của BC.

a) Chứng minh \(AH \bot BC\).

b) Trên tia đối của tia BC lấy điểm M; trên tia đối của tia CB lấy điểm N sao cho \(BM = CN\). Chứng minh rằng \(\Delta ABM = \Delta ACN\).

c) Gọi I là điểm trên AM, K là điểm trên AN sao cho \(BI \bot AM;CK \bot AN\). Chứng minh rằng tam giác AIK cân tại A, từ đó suy ra IK//MN.

Phương pháp giải - Xem chi tiết

a) Tam giác ABC cân tại A nên AH là đường trung tuyến đồng thời là đường cao.

b) + Vì \(\widehat {ABM} + \widehat {ABC} = {180^o}\), \(\widehat {ACN} + \widehat {ACB} = {180^o}\), \(\widehat {ABC} = \widehat {ACB}\) nên \(\widehat {ABM} = \widehat {ACN}\).

+ Chứng minh \(\Delta ABM = \Delta ACN\) (c.g.c).

c) + \(\Delta BIM = \Delta CKN\) (cạnh huyền – góc nhọn) nên \(MI = NK\). Mà \(AM = AN\) nên \(AI = AK\), suy ra \(\Delta AIK\) cân tại A. Suy ra \(\widehat {AIK} = \frac{{{{180}^o} - \widehat {IAK}}}{2}\).

+ Chứng minh \(\Delta AMN\) cân tại A nên \(\widehat {AMN} = \frac{{{{180}^o} - \widehat {MAN}}}{2}\). Suy ra \(\widehat {AIK} = \widehat {AMN}\) suy ra IK//MN.

Lời giải chi tiết

a) \(\Delta \)ABC cân tại A (giả thiết)

Mà AH là đường trung tuyến (H là trung điểm của BC)

Nên AH là đường cao của \(\Delta ABC\) (tính chất tam giác cân).

Vậy \(AH \bot BC\).

b) Ta có: \(\widehat {ABM} + \widehat {ABC} = {180^o}\) (hai góc kề bù), \(\widehat {ACN} + \widehat {ACB} = {180^o}\) (hai góc kề bù).

Mà \(\widehat {ABC} = \widehat {ACB}\) nên \(\widehat {ABM} = \widehat {ACN}\)

\(\Delta ABM\) và \(\Delta ACN\) có:

\(AB = AC\) (\(\Delta ABC\) cân tại đỉnh A).

\(\widehat {ABM} = \widehat {ACN}\) (chứng minh trên)

\(BM = CN\) (giả thiết)

Nên \(\Delta ABM = \Delta ACN\) (c.g.c).

c) Ta có \(\Delta ABM = \Delta ACN\) (chứng minh trên) suy ra \(\widehat {BMI} = \widehat {CNK}\) (hai góc tương ứng) và \(AM = AN\) (hai cạnh tương ứng).

\(\Delta BIM\left( {\widehat {BIM} = {{90}^o}} \right)\) và \(\Delta CKN\left( {\widehat {CKN} = {{90}^o}} \right)\) có:

\(BM = CN\) (giả thiết)

\(\widehat {BMI} = \widehat {CNK}\) (chứng minh trên)

Nên \(\Delta BIM = \Delta CKN\) (cạnh huyền – góc nhọn).

Suy ra \(MI = NK\) (hai cạnh tương ứng).

Mà \(AM = AN\) (chứng minh trên) nên \(AI = AK\), suy ra \(\Delta AIK\) cân tại A (dấu hiệu nhận biết tam giác cân).

Ta có \(AM = AN\)(chứng minh trên) nên \(\Delta AMN\) cân tại A (dấu hiệu nhận biết tam giác cân).

Suy ra \(\widehat {AMN} = \frac{{{{180}^o} - \widehat {MAN}}}{2}\).

Ta có \(\Delta AIK\) cân tại A (chứng minh trên) nên \(\widehat {AIK} = \frac{{{{180}^o} - \widehat {IAK}}}{2}\).

Từ đó \(\widehat {AIK} = \widehat {AMN}\left( { = \frac{{{{180}^o} - \widehat {IAK}}}{2}} \right)\)

Mà hai góc này ở vị trí đồng vị nên IK//MN (dấu hiệu nhận biết hai đường thẳng song song).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 10 trang 110, 111 vở thực hành Toán 7 tập 2
Cho tam giác ABC vuông tại A. Gọi D là điểm thuộc cạnh BC sao cho (BD = BA) và H là trung điểm của AD. Tia BH cắt AC tại E. Tia DE cắt BA tại M. Chứng minh rằng: a) (Delta ABH = Delta DBH). b) Tam giác AED cân. c) (EM > ED). d) Tam giác BCM là tam giác đều và (CE = 2EA), biết (widehat {ABC} = {60^o}).
Giải bài 11 trang 111, 112 vở thực hành Toán 7 tập 2
Bình thu thập số liệu về số học sinh phổ thông của cả nước từ năm 2015 đến năm 2020 và vẽ được biểu đồ dưới đây: a) Số học sinh phổ thông cả nước từ năm 2015 đến năm 2020 có xu thế tăng hay giảm? b) Hãy lập bảng thống kê về số lượng học sinh phổ thông của cả nước từ năm 2015 đến năm 2020. c) Theo em, Bình đã dùng cách nào trong các cách thu thập dữ liệu đã học để có được số liệu trên?
Giải bài 12 trang 112, 113 vở thực hành Toán 7 tập 2
Biểu đồ sau đây cho biết tổng số huy chương thế giới mà thể thao Việt Nam giành được trong các năm từ 2015 đến 2019: a) Lập bảng thống kê về số huy chương thế giới mà thể thao Việt Nam giành được trong các năm từ 2015 đến 2019. b) Trong các năm trên, năm nào thể thao Việt Nam giành được ít huy chương thế giới nhất? c) Tỉ lệ các loại huy chương thế giới của thể thao Việt Nam trong năm 2019 được cho trong biểu đồ sau: Tính số lượng mỗi loại huy chương thế giới mà thể thao Việt Nam giành được t
Giải bài 13 trang 113, 114 vở thực hành Toán 7 tập 2
Trong trò chơi Vòng quay may mắn, người chơi sẽ quay một bánh xe hình tròn. Bánh xe được chia làm 12 hình quạt bằng nhau như hình dưới. Trong mỗi hình quạt có ghi số điểm mà người chơi sẽ nhận được. Có hai hình quạt ghi 100 điểm; hai hình quạt ghi 200 điểm; hai hình quạt ghi 300 điểm; hai hình quạt ghi 400 điểm; một hình quạt ghi 500 điểm; hai hình quạt ghi 1 000 điểm; một hình quạt ghi 2 000 điểm. Khi bánh xe dừng lại, mũi tên (đặt cố định ở phía trên) chỉ vào hình quạt nào thì người chơi nhận
Giải bài 8 trang 107,108 vở thực hành Toán 7 tập 2
Cho tam giác ABC. Gọi D là trung điểm của AB. Trên tia đối của tia DC, lấy điểm M sao cho (DM = DC). a) Chứng minh rằng (Delta ADM = Delta BDC). Từ đó suy ra (AM = BC) và AM//BC. b) Gọi E là trung điểm của AC. Trên tia đối của tia EB lấy điểm N sao cho (EN = EB). Chứng minh rằng AN//BC. c) Chứng minh rằng ba điểm M, A, N thẳng hàng và A là trung điểm của đoạn MN.
Giải bài 7 trang 107 vở thực hành Toán 7 tập 2
Người ta đổ đầy nước vào một cái bể hình hộp chữ nhật, sau đó nhấn chìm một khối lập phương (đặc) có độ dài các cạnh bằng x(dm) vào trong bể. Biết rằng chiều rộng, chiều dài và chiều cao của bể lần lượt bằng (x + 1,x + 3) và (x + 2) (xem dưới đây). a) Tìm đa thức biểu thị lượng nước còn lại trong bể. b) Xác định bậc, hệ số cao nhất và hệ số tự do của đa thức trong câu a. c) Sử dụng kết quả câu a để tính lượng nước còn lại trong bể (đơn vị (d{m^3})) khi (x = 7left( {dm} right)).
Giải bài 6 trang 105, 106 vở thực hành Toán 7 tập 2
Cho hai đa thức (A = 6{x^3} - 4{x^2} - 12x - 7) và (B = 2{x^2} - 7). a) Xác định hệ số cao nhất và hệ số tự do trong mỗi đa thức đã cho. b) Tính giá trị của đa thức (A + B) tại (x = - 2). c) Chứng minh rằng (x = 0,x = - 1) và (x = 2) là ba nghiệm của đa thức (A - B). d) Trình bày phép nhân A.B bằng hai cách. e) Tìm đa thức R có bậc nhỏ hơn 2 sao cho hiệu (A - R) chia hết cho B.
Giải bài 5 trang 105 vở thực hành Toán 7 tập 2
Ba khối 6, 7, 8 của một trường Trung học cơ sở tham gia quyên góp vở tặng các bạn vùng khó khăn. Biết rằng số vở quyên góp được của ba khối theo thứ tự tỉ lệ thuận với 8, 7, 6 và số vở khối 8 quyên góp được ít hơn số vở khối 6 quyên góp được là 80 quyển. Hỏi mỗi khối quyên góp được bao nhiêu quyển vở?
Giải bài 4 trang 105 vở thực hành Toán 7 tập 2
Hai người thợ cùng làm tổng cộng được 136 sản phẩm (thời gian làm như nhau). Hỏi mỗi người thợ làm được bao nhiêu sản phẩm, biết rằng người thợ thứ nhất làm một sản phẩm mất 9 phút, còn người thứ hai mất 8 phút?
Giải bài 3 trang 104, 105 vở thực hành Toán 7 tập 2
a) Tìm x, biết: (frac{2}{5}x + frac{3}{2} = frac{3}{5} - left( { - frac{1}{4}} right)). b) Có hay không số x thỏa mãn điều kiện (left| x right| + frac{1}{5} = - left( {frac{1}{2} - frac{1}{3}} right))? c) Hãy ước tính (không tra bảng hay máy tính) số dương x (lấy đến một chữ số sau dấu phẩy) sao cho ({x^2} = 13). Sau đó dùng máy tính cầm tay (hoặc tra bảng) để tính x, chính xác đến hàng phần chục, để kiểm tra xem con số em ước tính chênh lệch bao nhiêu so với kết quả bằng m
Giải bài 2 trang 104 vở thực hành Toán 7 tập 2
Tính một cách hợp lí a) (frac{5}{{11}} - frac{{10}}{{19}} + 1,5 + frac{{17}}{{11}} - frac{9}{{19}}); b) (2frac{3}{5}.left( { - frac{2}{3}} right) - 2frac{1}{3}.left( { - frac{2}{3}} right) + {left( {frac{2}{3}} right)^2}).
Giải bài 1 trang 104 vở thực hành Toán 7 tập 2
Tính giá trị của các biểu thức sau: a) (sqrt {25} + {left( {{2^2}.3} right)^2}.{left( { - frac{1}{4}} right)^2} + {2020^0} + left| { - frac{1}{4}} right|); b) (frac{{{3^2} - 0,25.left( {7,5 - 5,1} right)}}{{ - 6,2 + 2.left( {0,5 + 1,6} right)}}).