Giải bài 6 trang118 vở thực hành Toán 9 tập 2

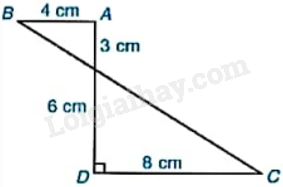
Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng.

Tổng hợp đề thi học kì 2 lớp 9 tất cả các môn - Kết nối tri thức

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Tính thể tích của hình tạo thành khi cho hình ABCD quay quanh AD một vòng.

Phương pháp giải - Xem chi tiết

Thể tích của hình nón bán kính r và chiều cao h là: \(V = \frac{1}{3}\pi {r^2}h\).

Lời giải chi tiết

Hình tạo thành là hai hình nón. Hình nón 1 có: \({R_1} = 8{\rm{\;cm}},{h_1} = 6{\rm{\;cm}}\); hình nón 2 có: \({R_2} = 4{\rm{\;cm}},{h_2} = 3{\rm{\;cm}}\).

Thể tích của hình nón 1 là: \({V_1} = \frac{1}{3}\pi R_1^2{h_1} = \frac{1}{3}\pi \cdot {8^2} \cdot 6 = 128\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).

Thể tích của hình nón 2 là: \({V_2} = \frac{1}{3}\pi {R_2}{\;^2}{h_2} = \frac{1}{3}\pi \cdot {4^2} \cdot 3 = 16\pi \;\,\,\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).

Thể tích hình tạo thành là: \(V = {V_1} + {V_2} = 128\pi + 16\pi = 144\pi \,\,\;\left( {{\rm{c}}{{\rm{m}}^3}} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 7 trang 118 vở thực hành Toán 9 tập 2
Một khối gỗ có dạng hình trụ có bán kính đáy là 30cm và chiều cao là 120cm. a) Tính thể tích của khối gỗ đó (làm tròn kết quả tới hàng phần trăm của (c{m^3})). b) Nếu sơn kín các mặt của khối gỗ thì diện tích cần sơn bằng bao nhiêu? (Làm tròn kết quả tới hàng đơn vị của (c{m^2})).
Giải bài 8 trang 118, 119 vở thực hành Toán 9 tập 2
Tam giác ABC cân tại A, đường cao AH, có (AB = 5cm,BC = 8cm). Quay tam giác ABC một vòng quanh cạnh AH ta được một hình nón. a) Tính thể tích của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^3})). b) Tính diện tích toàn phần của hình nón (làm tròn kết quả đến hàng phần trăm của (c{m^2})).
Giải bài 5 trang 117 vở thực hành Toán 9 tập 2
Một dụng cụ gồm một phần có dạng hình trụ và một phần có dạng hình nón với các kích thước như hình bên. a) Tính thể tích của dụng cụ này. b) Tính diện tích mặt ngoài của dụng cụ (không tính đáy của dụng cụ).
Giải bài 4 trang 117 vở thực hành Toán 9 tập 2
Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật. Hộp giấy có chiều dài bằng 0,6m, đáy là hình vuông cạnh 4cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
Giải bài 3 trang 116, 117 vở thực hành Toán 9 tập 2
Khi cho tam giác SOA vuông tại O quay quanh cạnh SO một vòng, ta được một hình nón. Biết (OA = 8cm), (SA = 17cm). a) Tính diện tích xung quanh của hình nón. b) Tính thể tích của hình nón.
Giải bài 2 trang 116 vở thực hành Toán 9 tập 2
Cho hình chữ nhật ABCD có (AB = 3cm,BC = 4cm). Quay hình chữ nhật quanh cạnh AB một vòng, ta được một hình trụ. Tính diện tích xung quanh và thể tích của hình trụ tạo thành.
Giải bài 1 trang 115 vở thực hành Toán 9 tập 2
Thay dấu “?” bằng giá trị thích hợp và hoàn thành bảng sau vào vở:
Giải câu hỏi trắc nghiệm trang 115 vở thực hành Toán 9 tập 2
Cho hình chữ nhật ABCD có (AB = 3cm,BC = 5cm). Quay hình chữ nhật xung quanh cạnh AB ta được hình trụ có bán kính đáy bằng A. 3cm. B. 4cm. C. 5cm. D. 8cm.