Giải bài 5.31 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1

Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm). a) Chứng minh rằng (PO bot AB). b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO. c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.

Đề bài

Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm).

a) Chứng minh rằng \(PO \bot AB\).

b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO.

c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.

Phương pháp giải - Xem chi tiết

a) + Chứng minh \(PA = PB\) và PO là tia phân giác của góc APB.

+ Chứng minh tam giác PAB cân tại P, suy ra PO là đường trung trực của tam giác AP nên \(PO \bot AB\).

b) + Chứng minh C thuộc (O).

+ Chứng minh tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.

c) + Chứng minh \(PA \bot OA\).

+ Áp dụng định lí Pythagore vào tam giác OAP vuông tại tính được PA, suy ra, \(PA = PB = 4cm\).

+ Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).

+ \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}}\) nên tính được AB.

Lời giải chi tiết

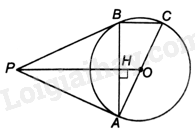
a) Vì PA và PB là hai tiếp tuyến cắt nhau tại P của (O) nên \(PA = PB\), PO là tia phân giác của góc APB.

Vì \(PA = PB\) nên tam giác PAB cân tại P. Do đó, PO là đường phân giác đồng thời là đường trung trực của tam giác ABP. Suy ra: \(PO \bot AB\).

b) Vì C là điểm đối xứng với A qua O nên \(OA = OC\). Do đó, C thuộc (O).

Vì \(OB = OC = OA = \frac{1}{2}AC\) nên tam giác BAC có trung tuyến BO có độ dài bằng nửa độ dài cạnh AC nên tam giác ABC vuông tại B. Do đó, \(BA \bot BC\). Mà \(PO \bot AB\)(cmt) nên BC//PO.

c) Vì PA tiếp xúc với (O) tại A nên \(PA \bot OA\).

Áp dụng định lí Pythagore vào tam giác OAP vuông tại A có: \(O{A^2} + A{P^2} = O{P^2}\) nên \(PA = \sqrt {O{P^2} - O{A^2}} = \sqrt {{5^2} - {3^2}} = 4\left( {cm} \right)\)

Do đó, \(PA = PB = 4cm\)

Gọi H là giao điểm của PO và AB. Theo a ta có: \(AH \bot OP\) và \(AB = 2AH\).

Ta có: \(AH.OP = OA.PA\left( { = 2{S_{\Delta AOP}}} \right)\) nên \(AH = \frac{{OA.AP}}{{OP}} = \frac{{3.4}}{5} = 2,4\left( {cm} \right)\).

Do đó, \(AB = 2AH = 2.2,4 = 4,8\left( {cm} \right)\).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5.32 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Từ B và từ C kẻ hai đường thẳng tiếp xúc với đường tròn (A; AH) lần lượt tại D và E. Chứng minh rằng: a) Hai điểm D và E đối xứng với nhau qua A; b) DE tiếp xúc với đường tròn đường kính BC.
Giải bài 5.33 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a//b. Gọi C là một điểm tùy ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N. a) Chứng minh AB là một đường kính của (O). b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng (D in left( O right),P in b) và (Q in a). c) Chứng minh rằng PQ tiếp xúc với (O) tại D. d) Chứng minh tứ giác MNPQ là một hình thoi.
Giải bài 5.34 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm (B in left( O right)) và (C in left( {O'} right)) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C. a) Chứng minh góc BAC là góc vuông. b) Cho biết (R = 3cm), (R' = 1cm) và BC cắt OO’ tại D. Tính độ dài đoạn OD.
Giải bài 5.35 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B. a) Chứng minh rằng MA và MB là hai tiếp tuyến của (N). b) Đường thẳng qua N và vuông góc với NA cắt MB tại C. Chứng minh hai điểm M và N đối xứng với nhau qua OC. c) Đường thẳng qua M và vuông góc với MA cắt NB tại D. Chứng minh ba điểm O, C và D thẳng hàng.
Giải bài 5.30 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác vuông ABC ((widehat A = {90^o})) có (widehat C = {30^o}) và AB=3cm. Đường phân giác của góc B cắt AC tại D. a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC. b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy. c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Giải bài 5.29 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD. a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE. b) Chứng minh rằng tứ giác ABCD là một hình thang cân. c) Biết rằng (AB = 12cm) và (widehat {COD} = {100^o}). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC. d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
Giải bài 5.28 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hình thang cân ABCD (AB//CD). a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d). b) Giải thích tại sao nếu một đường tròn đi qua ba điểm A, B và C thì nó cũng đi qua điểm D.
Giải bài 5.27 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC có (AB < AC) và đường cao AH (H.5.12). a) Trong các điểm B, H và C, điểm nào nằm trong, điểm nào nằm trên và điểm nào nằm ngoài đường tròn (A; AB)? Vì sao? b) Xác định ví trị của điểm D trên đoạn AC trong mỗi trường hợp sau: • Đường tròn (A) và đường tròn (C; CD) tiếp xúc với nhau; • Đường tròn (A) và đường tròn (C; CD) cắt nhau; • Đường tròn (A) và đường tròn (C; CD) không giao nhau.
Giải câu hỏi trắc nghiệm trang 69, 70 sách bài tập toán 9 - Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; (sqrt 5 )), hai điểm (Aleft( { - sqrt 3 ;1} right)) và B(-1; 2). Khi đó xảy ra: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm trong (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm ngoài (O), điểm B nằm trên (O).