Giải bài 5.27 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1

Cho tam giác ABC có (AB < AC) và đường cao AH (H.5.12). a) Trong các điểm B, H và C, điểm nào nằm trong, điểm nào nằm trên và điểm nào nằm ngoài đường tròn (A; AB)? Vì sao? b) Xác định ví trị của điểm D trên đoạn AC trong mỗi trường hợp sau: • Đường tròn (A) và đường tròn (C; CD) tiếp xúc với nhau; • Đường tròn (A) và đường tròn (C; CD) cắt nhau; • Đường tròn (A) và đường tròn (C; CD) không giao nhau.

Đề bài

Cho tam giác ABC có \(AB < AC\) và đường cao AH (H.5.12).

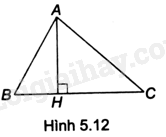
a) Trong các điểm B, H và C, điểm nào nằm trong, điểm nào nằm trên và điểm nào nằm ngoài đường tròn (A; AB)? Vì sao?

b) Xác định ví trị của điểm D trên đoạn AC trong mỗi trường hợp sau:

- Đường tròn (A) và đường tròn (C; CD) tiếp xúc với nhau;

- Đường tròn (A) và đường tròn (C; CD) cắt nhau;

- Đường tròn (A) và đường tròn (C; CD) không giao nhau.

Phương pháp giải - Xem chi tiết

a) + Điểm B nằm trên đường tròn (A; AB).

+ Chứng minh \(AH < AB\). Do đó, điểm H nằm trong đường tròn (A; AB).

+ Vì \(AB < AC\) nên điểm C nằm ngoài đường tròn (A; AB).

b) Hai đường tròn (O; R) và (O’; r) (với \(R > r\)). Khi đó:

+ Hai đường tròn ở ngoài nhau khi \(OO' > R + r\).

+ Hai đường tròn tiếp xúc ngoài khi \(OO' = R + r\).

+ Hai đường tròn cắt nhau khi \(R - r < OO' < R + r\).

+ Hai đường tròn tiếp xúc trong khi \(OO' = R - r\).

+ Đường tròn (O) đựng (O’) khi \(OO' < R - r\).

Lời giải chi tiết

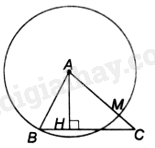
a) Điểm B nằm trên đường tròn (A; AB).

Vì \(AB < AC\) nên điểm C nằm ngoài đường tròn (A; AB).

Tam giác AHB vuông tại H nên \(AH < AB\). Do đó, điểm H nằm trong đường tròn (A; AB).

b) Do điểm C nằm ngoài đường tròn (A; AB) nên AH cắt đường tròn đó tại một điểm nằm giữa A và C; gọi điểm đó là điểm M.

- Đường tròn (A) và đường tròn (C; CD) tiếp xúc với nhau khi D trùng với M.

- Đường tròn (A) và đường tròn (C; CD) cắt nhau khi D nằm giữa A và M.

- Đường tròn (A) và đường tròn (C; CD) không giao nhau khi D nằm giữa C và M.

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5.28 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hình thang cân ABCD (AB//CD). a) Chứng minh rằng đường trung trực d của AB cũng là đường trung trực của CD (từ đó suy ra hai điểm A và B đối xứng với nhau, C và D đối xứng với nhau qua d). b) Giải thích tại sao nếu một đường tròn đi qua ba điểm A, B và C thì nó cũng đi qua điểm D.
Giải bài 5.29 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Giả sử CD là một dây song song với đường kính AB của đường tròn (O) sao cho ABCD là một tứ giác lồi. Gọi E là trung điểm của đoạn CD. a) Chứng minh rằng A đối xứng với B và C đối xứng với D qua đường thẳng OE. b) Chứng minh rằng tứ giác ABCD là một hình thang cân. c) Biết rằng (AB = 12cm) và (widehat {COD} = {100^o}). Tính độ dài cung (nhỏ) AD và cung (lớn) ABC. d) Với giả thiết ở câu c, tính diện tích hình quạt tròn ứng với cung nhỏ BD.
Giải bài 5.30 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác vuông ABC ((widehat A = {90^o})) có (widehat C = {30^o}) và AB=3cm. Đường phân giác của góc B cắt AC tại D. a) Chứng minh rằng đường tròn (D; DA) tiếp xúc với cạnh BC. b) Tính độ dài cung nằm trong góc BDC của đường tròn (D; DA) và diện tích hình quạt tròn tương ứng với cung ấy. c) Tính diện tích hình vành khuyên tạo bởi hai đường tròn (D; DA) và (D; DC).
Giải bài 5.31 trang 71 sách bài tập toán 9 - Kết nối tri thức tập 1
Từ điểm P nằm ngoài đường tròn (O), kẻ hai tiếp tuyến PA và PB đến đường tròn (A và B là hai tiếp điểm). a) Chứng minh rằng (PO bot AB). b) Gọi C là điểm đối xứng với A qua O. Chứng minh rằng BC//PO. c) Tính độ dài các cạnh của tam giác PAB, biết OA=3cm và OP=5cm.
Giải bài 5.32 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Từ B và từ C kẻ hai đường thẳng tiếp xúc với đường tròn (A; AH) lần lượt tại D và E. Chứng minh rằng: a) Hai điểm D và E đối xứng với nhau qua A; b) DE tiếp xúc với đường tròn đường kính BC.
Giải bài 5.33 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn (O), đường thẳng a tiếp xúc với (O) tại A, đường thẳng b tiếp xúc với (O) tại B sao cho a//b. Gọi C là một điểm tùy ý thuộc (O), khác A và B. Tiếp tuyến c của (O) tại C cắt a và b lần lượt tại M và N. a) Chứng minh AB là một đường kính của (O). b) Gọi D, P và Q lần lượt là các điểm đối xứng với C, M và N qua tâm O. Chứng minh rằng (D in left( O right),P in b) và (Q in a). c) Chứng minh rằng PQ tiếp xúc với (O) tại D. d) Chứng minh tứ giác MNPQ là một hình thoi.
Giải bài 5.34 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho hai đường tròn (O; R) và (O’; R’) tiếp xúc ngoài với nhau tại A, hai điểm (B in left( O right)) và (C in left( {O'} right)) sao cho B và C nằm cùng phía đối với đường thẳng OO’ và OB//O’C. a) Chứng minh góc BAC là góc vuông. b) Cho biết (R = 3cm), (R' = 1cm) và BC cắt OO’ tại D. Tính độ dài đoạn OD.
Giải bài 5.35 trang 72 sách bài tập toán 9 - Kết nối tri thức tập 1
Cho đường tròn tâm O, đường kính MN. Một đường tròn (N) cắt (O) tại A và B. a) Chứng minh rằng MA và MB là hai tiếp tuyến của (N). b) Đường thẳng qua N và vuông góc với NA cắt MB tại C. Chứng minh hai điểm M và N đối xứng với nhau qua OC. c) Đường thẳng qua M và vuông góc với MA cắt NB tại D. Chứng minh ba điểm O, C và D thẳng hàng.
Giải câu hỏi trắc nghiệm trang 69, 70 sách bài tập toán 9 - Kết nối tri thức tập 1
Trong mặt phẳng tọa độ Oxy, cho đường tròn (O; (sqrt 5 )), hai điểm (Aleft( { - sqrt 3 ;1} right)) và B(-1; 2). Khi đó xảy ra: A. Điểm A nằm trong (O), điểm B nằm ngoài (O). B. Điểm A nằm trong (O), điểm B nằm trên (O). C. Điểm A nằm trên (O), điểm B nằm trong (O). D. Điểm A nằm ngoài (O), điểm B nằm trên (O).