Giải bài 4 trang 92 vở thực hành Toán 9

Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc ({20^o}) và chắn ngang lối đi một đoạn 5m (H.4.42). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

Đề bài

Một cây cao bị gãy, ngọn cây đổ xuống mặt đất. Ba điểm: gốc cây, điểm gãy, ngọn cây tạo thành một tam giác vuông. Đoạn cây gãy tạo với mặt đất góc \({20^o}\) và chắn ngang lối đi một đoạn 5m (H.4.42). Hỏi trước khi bị gãy, cây cao khoảng bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?

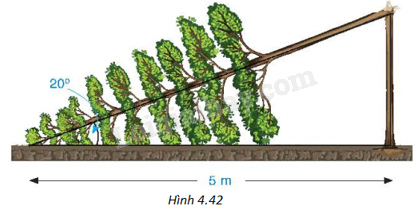
Phương pháp giải - Xem chi tiết

+ Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.

+ Trong tam giác ABC vuông tại A, ta có: \(AB = AC.\tan C\) tính được AB, \(\cos \widehat {ACB} = \frac{{AC}}{{BC}}\) tính được CB.

+ Chiều cao của cây trước khi đổ gãy là: \(AB + BC\).

Lời giải chi tiết

(H.4.43)

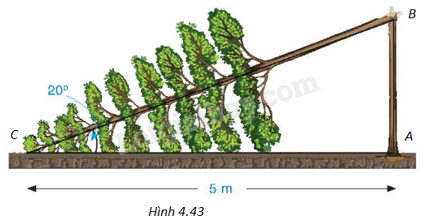
Gọi A là gốc cây, B là điểm cây gãy, C là ngọn cây.

Trong tam giác ABC vuông tại A, ta có \(AB = AC.\tan C = 5.\tan {20^o}\), \(\cos \widehat {ACB} = \frac{{AC}}{{BC}} = \frac{5}{{CB}}\) nên \(BC = \frac{5}{{\cos {{20}^o}}}\).

Do đó, chiều cao của cây trước khi đổ gãy là

\(AB + BC = 5.\tan {20^o} + \frac{5}{{\cos {{20}^o}}} \\= 5\left( {\tan {{20}^o} + \frac{1}{{\cos {{20}^o}}}} \right) \approx 7,1\left( m \right)\)

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 5 trang 92 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, có (widehat B = alpha ) (H.4.44).
Giải bài 6 trang 93 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, biết (AB = 6cm,BC = 11cm). a) Giải tam giác vuông ABC. b) Tính độ dài đường cao AH, đường phân giác AD. (Kết quả về cạnh làm tròn đến chữ số thập phân thứ nhất, kết quả về góc làm tròn đến độ).
Giải bài 7 trang 94 vở thực hành Toán 9
Đố vui. Chu vi Trái Đất bằng bao nhiêu? Vào khoảng năm 200 trước Công nguyên, Eratosthenes (Ơ-ra-tô-xten), một nhà toán học và thiên văn học người Hy Lạp, đã ước lượng được “chu vi” của Trái Đất (chu vi của đường Xích Đạo) nhờ hai quan sát sau: 1. Hồi đó, hằng năm cứ vào trưa ngày Hạ Chí (21/6), người ta thấy tia sáng mặt trời chiếu thẳng xuống đáy một giếng sâu nổi tiếng ở thành phố Syene (Xy-en), tức là tia sáng chiếu thẳng đứng. 2. Cũng vào trưa một ngày Hạ chí, ở thành phố Alexandria (A-l
Giải bài 8 trang 95 vở thực hành Toán 9
Cho tam giác ABC vuông tại A, kẻ đường cao AH. Biết (AH = 4,CH = 3) (H.4.48). a) Giải tam giác ABC (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). b) Giải tam giác ABH (Góc làm tròn đến độ, cạnh làm tròn đến chữ số thập phân thứ nhất). c) Tính giá trị biểu thức (M = frac{{sin B + 3cos B}}{{cos B}}).
Giải bài 9 trang 96 vở thực hành Toán 9
Cho tam giác ABC có (widehat {ABC} = {45^o}). Kẻ đường cao AH ((H in BC)). Biết (BH = 20,CH = 21) (H.4.49). a) Tính AB, AC. b) Tính góc C và góc A.
Giải bài 3 trang 91 vở thực hành Toán 9
Hình 4.40 là mô hình của một túp lều. Tìm góc (alpha ) giữa cạnh mái lều và mặt đất (làm tròn kết quả đến phút).
Giải bài 2 trang 91 vở thực hành Toán 9
Xét các tam giác vuông có một góc nhọn bằng hai lần góc nhọn còn lại. Hỏi các tam giác đó có đồng dạng với nhau không? Tính sin và côsin của góc nhọn lớn hơn.
Giải bài 1 trang 91 vở thực hành Toán 9
Cho tam giác ABC vuông tại A có (widehat B = {60^o},BC = 20cm). a) Tính AB, AC. b) Kẻ đường cao AH của tam giác. Tính AH, HB, HC.
Giải câu hỏi trắc nghiệm trang 90 vở thực hành Toán 9
Trong Hình 4.35, (cos alpha ) bằng A. (frac{5}{3}). B. (frac{3}{4}). C. (frac{3}{5}). D. (frac{4}{5}).