 SBT Toán 12 - Giải SBT Toán 12 - Kết nối tri thức
SBT Toán 12 - Giải SBT Toán 12 - Kết nối tri thức
 Bài 6. Vecto trong không gian - SBT Toán 12 Kết nối tri..
Bài 6. Vecto trong không gian - SBT Toán 12 Kết nối tri..
Giải bài 2.15 trang 46 sách bài tập toán 12 - Kết nối tri thức
Cho hình chóp S.ABC có (SA = SB = SC) và (widehat {ASB} = widehat {BSC} = widehat {CSA}). Chứng minh rằng (overrightarrow {SA} cdot overrightarrow {BC} = overrightarrow {SB} cdot overrightarrow {AC} = overrightarrow {SC} cdot overrightarrow {AB} ).
Đề bài
Cho hình chóp S.ABC có \(SA = SB = SC\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA}\).
Chứng minh rằng \(\overrightarrow {SA} \cdot \overrightarrow {BC} = \overrightarrow {SB} \cdot \overrightarrow {AC} = \overrightarrow {SC} \cdot \overrightarrow {AB} = 0 \).
Phương pháp giải - Xem chi tiết
Sử dụng định lý ba đường vuông góc để tìm hình chiếu của \(S\) trên \(\left( {ABC} \right)\), tiếp tục dùng định lý này để chứng minh \(SA \bot BC\), \(SB \bot AC\) và \(SC \bot AB\). Từ đó suy ra các tích vô hướng của từng cặp vuông góc đều bằng 0, do đó chúng bằng nhau.
Lời giải chi tiết
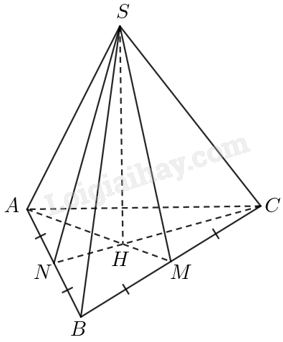
Theo đề bài ta có ba tam giác \(SAB,{\rm{ }}SAC,{\rm{ }}SAB\) đôi một bằng nhau theo trường hợp cạnh-góc-cạnh. Do đó \(AB = BC = AC\) (cạnh tương ứng), suy ra tam giác \(ABC\)là tam giác đều.
Giả sử \(H\) là hình chiếu của \(S\) trên \(\left( {ABC} \right)\), kẻ \(HM \bot BC\) với \(M \in BC\) ta có \(SM \bot BC\).
Mặt khác, tam giác \(SBC\) cân tại \(S\)(giả thiết \(SB = SC\)) suy ra \(M\) là trung điểm cạnh \(BC\).
Từ đó suy ra \(HM\) là một phần đường trung tuyến của tam giác \(ABC\).
Tương tự, kẻ \(HN \bot AB\) ta thu được \(HN\) là một phần đường trung tuyến của tam giác
\(ABC\). Do đó ta có \(H\) là trọng tâm tam giác \(ABC\).
Ta có \(AM\) là hình chiếu của \(SA\) trên \(\left( {ABC} \right)\) và \(AM \bot BC\) suy ra \(SA \bot BC\) do đó \(\overrightarrow {SA} \cdot \overrightarrow {BC} = 0\)
Chứng minh tương tự ta thu được \(SB \bot AC\) và \(SC \bot AB\).
Vậy \(\overrightarrow {SA} \cdot \overrightarrow {BC} = \overrightarrow {SB} \cdot \overrightarrow {AC} = \overrightarrow {SC} \cdot \overrightarrow {AB} = 0\).
- Giải bài 2.14 trang 46 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 2.13 trang 46 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 2.12 trang 46 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 2.11 trang 45 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 2.10 trang 45 sách bài tập toán 12 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4.39 trang 20 sách bài tập toán 12 - Kết nối tri thức
- Đề minh họa kiểm tra cuối học kì 2 - SBT Toán 12 Kết nối tri thức
- Giải bài 45 trang 56 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 44 trang 55 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 43 trang 55 sách bài tập toán 12 - Kết nối tri thức
- Đề minh họa kiểm tra cuối học kì 2 - SBT Toán 12 Kết nối tri thức
- Giải bài 45 trang 56 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 44 trang 55 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 43 trang 55 sách bài tập toán 12 - Kết nối tri thức
- Giải bài 42 trang 55 sách bài tập toán 12 - Kết nối tri thức












Danh sách bình luận