Giải bài 17 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2

Một công viên hình tam giác được bao quanh bởi ba con đường ML, LN, NM với kích thước (tính theo mét) được ghi trên bản vẽ trong Hình 7. Người ta muốn dựng một trụ đèn tại một điểm cách đều ba con đường. Xác định vị trí điểm cần tìm và tính khoảng cách từ điểm đó đến ba con đường.

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Một công viên hình tam giác được bao quanh bởi ba con đường ML, LN, NM với kích thước (tính theo mét) được ghi trên bản vẽ trong Hình 7. Người ta muốn dựng một trụ đèn tại một điểm cách đều ba con đường. Xác định vị trí điểm cần tìm và tính khoảng cách từ điểm đó đến ba con đường.

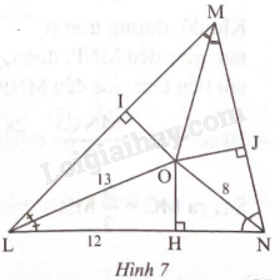
Phương pháp giải - Xem chi tiết

Xác định điểm O là tâm và tính r là bán kính của đường tròn nội tiếp tam giác MNL.

Lời giải chi tiết

Điểm O là điểm cần tìm để dựng trụ đèn và là tâm của đường tròn nội tiếp tam giác MNL. Khoảng cách r từ O đến ba con đường là bán kính của đường tròn nội tiếp tam giác MNL.

Áp dụng định lí Pythagore vào tam giác OLH vuông tại H, ta có:

r = OH = \(\sqrt {O{L^2} - L{H^2}} = \sqrt {{{13}^2} - {{12}^2}} = 5\) (m).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 16 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho đường tròn tâm O, đường kính AB. Gọi C là điểm chính giữa của cung AB. Trên đoạn thẳng AB lấy điểm E sao cho BE = AC. Tia AC và tia BD cắt nhau tại M. Vẽ EH vuông góc với AC tại H. Tia phân giác của góc (widehat {BAC}) cắt EH tại K và cắt đường tròn (O) tại D. Tia CK cắt AB tại I và cắt đường tròn (O) tại F. a) Chứng minh EH // BC. b) Tính số đo của (widehat {AMB}). c) Chứng minh (widehat {AEK} = widehat {AFK}). d) Chứng minh I là trung điểm của đoạn thẳng AE.
Giải bài 15 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác nhọn ABC (AB < AC) có hai đường cao BD và CE. a) Chứng minh bốn điểm B, C, D, E cùng thuộc đường tròn. b) Vẽ đường tròn (B; BD). Chứng minh AC là tiếp tuyến của đường tròn (B; BD). c) Đường tròn (B; BD) cắt CE tại K (K nằm giữa E và C). Qua D vẽ đường thẳng vuông góc với BC tại H và cắt đường thẳng AB tại M. Chứng minh (widehat {BMH} = widehat {BKH}).
Giải bài 14 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp.
Giải bài 13 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác ABC có (O) là đường tròn ngoại tiếp. Vẽ đường cao AH của tam giác ABC và đường kính AD của đường tròn (O). Biết AB = 8 cm; AC = 15 cm và AH = 5 cm. a) Chứng minh (Delta AHBbacksim Delta ACD). b) Tính độ dài bán kính của đường tròn
Giải bài 12 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho bát giác đều có tâm O và AB là một cạnh, OH là đoạn vuông góc kẻ từ O đến AB. a) (widehat {AOB} = {50^o}). b) OH = OA. sin 45o c) Phép quay 90o tâm O biến bát giác đều thành chính nó. d) AB = 2OA . sin 22,5o.
Giải bài 11 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O) có (widehat {ABC} = {80^o}) và (widehat {CDO} = {52^o}) (Hình 5). a) (widehat {ADC} = {160^o}) b) (widehat {AOC} = {160^o}) c) (widehat {AOD} = {84^o}) d) (widehat {COD} = {86^o})
Giải bài 10 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác ABC ngoại tiếp đường tròn (I; r); D, E, F lần lượt là các tiếp điểm của cạnh AB, BC, AC với đường tròn (I; r) (Hình 4). a) Ba đường trung trực của tam giác ABC cắt nhau tại I. b) AD = AF. c) BD + CF = BC d) IE = r
Giải bài 9 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho hình vuông ABCD có O là giao điểm của hai đường chéo. Phép quay tâm O biến hình vuông ABCD thành chính nó có góc quay là A. 45o B. 90o C. 135o D. 210o
Giải bài 8 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Gọi A, B, C là ba đỉnh liên tiếp của một đa giác đều có 10 cạnh. Số đo của (widehat {ABC}) là A. 144o B. 36o C. 72o D. 152o
Giải bài 7 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Số đo của (widehat {BCD}) trong Hình 3 là A. 100o B. 160o C. 80o D. 120o
Giải bài 6 trang 88 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tứ giác ABCD nội tiếp đường tròn (E). Số đo của các cung được cho trong Hình 2. Số đo của (widehat {BCD}) là A. 201o B. 100,5o C. 159o D. 79,5o
Giải bài tập 5 trang 87 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Số đo của (widehat C) trong Hình 1 là A. 110o B. 70o C. 140o D. 220o
Giải bài 4 trang 87 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tứ giác ABCD nội tiếp đường tròn (O; R) và (widehat A = {90^o}), BD = 12 cm. Độ dài của bán kính R là A. 12 cm B. 24 cm C. 6 cm D. (6sqrt 2 )cm
Giải bài 3 trang 87 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tứ giác MNPQ nội tiếp đường tròn (O; R) và (widehat M = {63^o}). Số đo của (widehat P) là A. 63o B. 117o C. 63o D. 126o
Giải bài 2 trang 87 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Tam giác đều cạnh bằng (8asqrt 3 ) có bán kính đường tròn nội tiếp là A. 4a B. 2a C. (4asqrt 3 ) D. (2asqrt 3 )
Giải bài 1 trang 87 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác vuông ABC có độ dài hai cạnh góc vuông là 5 cm, 12 cm. Bán kính R của đường tròn ngoại tiếp tam giác ABC có độ dài là A. 13 cm B. 10 cm C. 5 cm D. 6,5 cm