Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2

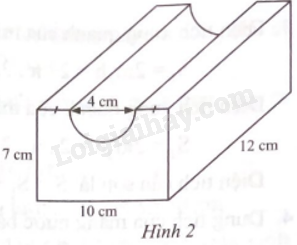
Một khối hộp chữ nhật đặc với kích thước ba cạnh là 12 cm, 10 cm, 7 cm bị khoét bởi một nửa hình trụ có đường kính 4 cm và chiều dài 12 cm (Hình 2). Tính a) Thể tích của khối còn lại b) Diện tích bề mặt của khối còn lại. (Làm tròn kết quả đến hàng đơn vị của xăngtimet khối, xăngtimet vuông).

Tổng hợp đề thi học kì 1 lớp 9 tất cả các môn - Chân trời sáng tạo

Toán - Văn - Anh - KHTN - Lịch sử và Địa lí

Đề bài

Một khối hộp chữ nhật đặc với kích thước ba cạnh là 12 cm, 10 cm, 7 cm bị khoét bởi một nửa hình trụ có đường kính 4 cm và chiều dài 12 cm (Hình 2). Tính

a) Thể tích của khối còn lại

b) Diện tích bề mặt của khối còn lại.

(Làm tròn kết quả đến hàng đơn vị của xăngtimet khối, xăngtimet vuông).

Phương pháp giải - Xem chi tiết

Diện tích xung quanh hình trụ: \({S_{xq}} = 2\pi rh\).

Diện tích toàn phần hình trụ: \({S_{tp}} = 2\pi rh + 2r{\pi ^2} = 2\pi r(r + h)\).

Thể tích hình hộp chữ nhật: V = cạnh.cạnh.cạnh

Thể tích hình trụ: \(V = \pi {r^2}h\).

Lời giải chi tiết

a) Thể tích của khối hộp chữ nhật khi chưa bị khoét là:

\({V_1} = 12.10.7 = 840\) (cm³).

Thể tích của nửa hình trụ là \({V_2} = \frac{1}{2}\pi {r^2}h = \frac{1}{2}\pi {.2^2}.12 = 24\pi \) (cm³).

Thể tích khối còn lại là: \(V = {V_1} - {V_2} = 840 - 24\pi \approx 765\)(cm³).

b) Diện tích toàn phần của khối hộp khi chưa bị khoét là:

\({S_1} = 2(7.10 + 12.10 + 7.12) = 548\) (cm²).

Diện tích xung qunah của nửa hình trụ là: \({S_2} = \pi rh = \pi .2.12 = 24\pi \)(cm²)

Diện tích hai đáy của nửa hình trụ là: \({S_3} = \pi {r^2} = 4\pi \) (cm²).

Diện tích mặt cắt dọc của nửa hình trụ là: \({S_4} = 4.12 = 48\) (cm²).

Diện tích bề mặt của khối còn lại là:

\(S = {S_1} + {S_2} - {S_3} - {S_4} = 548 + 24\pi - 4\pi - 48 \approx 563\) (cm²).

Bình luận

Chia sẻ

Bình chọn:

4.9 trên 7 phiếu

Bài tiếp theo

Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Một vật thể rắn hình chữ C dạng nửa hình trụ có bán kính bên trong là 8 cm và độ dày đồng đều 1,6 cm và chiều cao 10 cm (Hình 3). Tính thể tích của vật thể (kết quả làm tròn đến hàng đơn vị của xăngtimet khối).
Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Một cái lọ chứa nước bằng thiếc dạng hình trụ có đường kính bên trong là 18 cm, chiều cao mực nước trong lọ là 13,2 cm. Một quả cầu thép đường kính 12 cm được thả chìm hoàn toàn trong lọ nước sau khi thả quả cầu vào (kết quả làm tròn đến hàng phần trăm của xăngtimet).
Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Người ta làm nóng chảy một quả cầu kim loại đặc có bán kính 4 cm để chết tạo một vật thể đặc dạng hình nón có bán kính đáy 4 cm. Tìm chiều cao của vật thể mới tạo thành.
Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Một khối thuỷ tinh được tạo thành từ một phần dạng hình hộp chữ nhật có kích thước 6 cm, 16 cm, 9 cm và một phần dạng nửa hình trụ có đường kính đáy 6 cm, chiều cao 16 cm (Hình 1). Tính: a) Thể tích khối thuỷ tinh. b) Diện tích bề mặt của khối thuỷ tinh. (Làm tròn kết quả đến hàng đơn vị của xăngtimet khối, xăngtimet vuông).
Giải bài 11 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một hình trụ có đường kính đáy và chiều cao bằng đường kính của một hình cầu. a) Thể tích của hình trụ bằng 2 lần thể tích hình cầu. b) Thể tích của hình trụ bằng (frac{3}{2}) thể tích hình cầu. c) Diện tích mặt cầu bằng 2 lần tổng diện tích hai mặt đáy của trụ. d) Diện tích mặt cầu bằng diện tích xung quanh của hình trụ.
Giải bài 10 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một hình trụ và một hình nón có chiều cao và bán kính đáy cùng bằng 10 . a) Diện tích xung quanh của hình trụ gấp đôi diện tích xung quanh hình nón. b) Thể tích của hình trụ gấp đôi thể tích hình nón. c) Diện tích toàn phần của hình trụ gấp đôi diện tích toàn phần của hình nón. d) Thể tích của hình trụ gấp 3 lần thể tích hình nón.
Giải bài 9 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một mặt cầu có diện tích (576pi ) m2 . Thể tích của hình cầu đó là A. 2304 m3 B. (2304pi ) cm3 C. 2304 cm3 D. (2304pi ) m3
Giải bài 8 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một hình cầu có thể tích (36pi ) cm3 . Diện tích của mặt cầu đó là A. (36pi ) cm2 B. (36pi ) m2 C. (72pi ) cm2 D. (36) cm2
Giải bài 7 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một hình trụ có diện tích xung quanh là (50pi ) cm2 và bán kính đáy là 5 cm. Thể tích của hình trụ đó là A. (25pi ) cm3 B. (125) cm3 C. (125pi ) cm3 D. (100pi ) cm3
Giải bài 6 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho một hình nón có thể tích là (16pi ) cm3 và bán kính đáy là 4 cm. Diện tích xung quanh của hình nón đó là A. (40pi ) cm2 B. (60pi ) cm2 C. (80pi ) cm2 D. (20pi ) cm2
Giải bài tập 5 trang 107 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho hai hình nón có chiều cao bằng nhau, bán kính đáy của hình nón thứ nhất gấp đôi bán kính đáy của hình nón thứ hai. Tỉ số thể tích của hình nón thứ nhất và thứ hai là A. 1:1 B. 1:2 C. 2:1 D. 4:1
Giải bài tập 4 trang 107 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho hai hình trụ có bán kính đáy bằng nhau, chiều cao của hình trụ thứ nhất gấp đôi chiều cao của hình trụ thứ hai. Tỉ số thể tích của hình trụ thứ nhất và thứ hai là A. 1:1 B. 1:2 C. 2:1 D. 3:1
Giải bài tập 3 trang 107 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Diện tích mặt cầu bán kính 5 cm khoảng A. 78,54 cm2 B. 157,08 cm2 C. 235,56 cm2 D. 314,16 cm2
Giải bài 2 trang 107 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Thể tích của hình nón có bán kính đáy 5 cm, chiều cao 10 cm là: A. 25(pi ) cm3 B. 50(pi ) cm3 C.(frac{{250pi }}{3}) cm3 D. 100(pi ) cm3
Giải bài 1 trang 107 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Diện tích xung quanh của hình trụ có bán kính đáy 5 cm, chiều cao 10 cm là A. 100(pi ) cm2 B. 200(pi ) cm2 C. 300(pi ) cm2 D. 400(pi ) cm2