Giải bài 14 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp.
Tổng hợp đề thi giữa kì 2 lớp 9 tất cả các môn - Chân trời sáng tạo
Toán - Văn - Anh - KHTN
Đề bài
Cho hình thang cân ABCD có AB // CD. Chứng minh ABCD là tứ giác nội tiếp.
Phương pháp giải - Xem chi tiết
Chứng minh 4 điểm A, B, C, D cùng đường tròn (O; OA).
Lời giải chi tiết
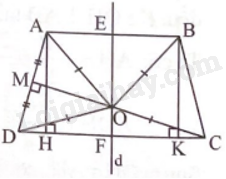
Từ A, B lần lượt kẻ AH, BK vuông góc với CD (H,K \( \in \)CD).
Ta có AD = BC và AH = BK, suy ra \(\Delta ADH = \Delta BCK\), suy ra DH = CK.
Gọi E, F lần lượt là trung điểm của AB và HK.
Ta có ABHK là hình chữ nhật, suy ra EF là đường trung trực của AB và HK, suy ra EF cũng là đường trung trực của CD.
Gọi M là trung điểm của AD. Vẽ đường trung trực MO của AD, MO cắt EF tại O.
Ta có OA = OB, OA = OD, OD = OC, suy ra OA = OB = OC = OD hay A, B, C, D cũng thuộc đường tròn (O; OA).
Vậy hình thang cân ABCD nội tiếp đường tròn (O; OA).
- Giải bài 15 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 17 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 89 sách bài tập toán 9 - Chân trời sáng tạo tập 2
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 9 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 4 trang 86 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 1 trang 98 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 16 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 15 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 14 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 13 trang 109 sách bài tập toán 9 - Chân trời sáng tạo tập 2
- Giải bài 12 trang 108 sách bài tập toán 9 - Chân trời sáng tạo tập 2













Danh sách bình luận