 SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo
SBT Toán 12 - giải SBT Toán 12 - Chân trời sáng tạo
 Bài 1. Tính đơn điệu và cực trị của hàm số - SBT Toán 1..
Bài 1. Tính đơn điệu và cực trị của hàm số - SBT Toán 1..
Giải bài 12 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
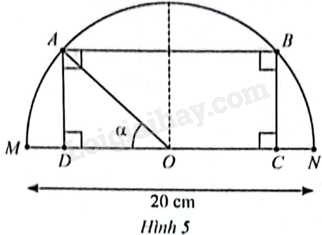
Cho điểm \(A\) di động trên nửa đường tròn tâm \(O\) đường kính \(MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha \) với \(0 \le \alpha \le \pi \). Lấy điểm \(B\) thuộc nửa đường tròn và \(C,D\) thuộc đường kính \(MN\) được xác định sao cho \(ABCD\) là hình chữ nhật. Khi \(A\) di động từ trái sang phải, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) tăng, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) giảm?
Đề bài
Cho điểm \(A\) di động trên nửa đường tròn tâm \(O\) đường kính \(MN = 20{\rm{ }}cm,\widehat {MOA} = \alpha \) với \(0 \le \alpha \le \pi \). Lấy điểm \(B\) thuộc nửa đường tròn và \(C,D\) thuộc đường kính \(MN\) được xác định sao cho \(ABCD\) là hình chữ nhật. Khi \(A\) di động từ trái sang phải, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) tăng, trong các khoảng nào của \(\alpha \) thì diện tích của hình chữ nhật \(ABCD\) giảm?
Phương pháp giải - Xem chi tiết
Lập hàm số \(y = f\left( \alpha \right)\) trên đoạn \(\left[ {0;\pi } \right]\), lập bảng biến thiên và tìm khoảng đồng biến, nghịch biến của hàm số.
Lời giải chi tiết
Ta có: \(A{\rm{D}} = OA\sin \alpha = 10\sin \alpha ;O{\rm{D}} = OA\cos \alpha = 10\cos \alpha ;C{\rm{D}} = 2{\rm{OD}} = 20\cos \alpha \).
Diện tích hình chữ nhật là: \(AD.C{\rm{D}} = 10\sin \alpha .20\cos \alpha = 200\sin \alpha \cos \alpha = 100\sin 2\alpha \).
Xét hàm số \(f\left( \alpha \right) = 100\sin 2\alpha \) trên đoạn \(\left[ {0;\pi } \right]\).
Ta có:
\(f'\left( \alpha \right) = 200\cos 2\alpha ;f'\left( \alpha \right) = 0 \Leftrightarrow \alpha = \frac{\pi }{4}\) hoặc \(\alpha = \frac{{3\pi }}{4}\).
Bảng biến thiên:
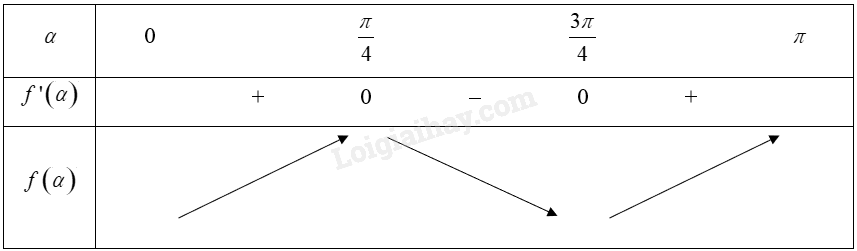
Vậy hàm số đồng biến trên các khoảng \(\left( {0;\frac{\pi }{4}} \right)\) và \(\left( {\frac{{3\pi }}{4};\pi } \right)\), hàm số nghịch biến trên khoảng \(\left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\).
Vậy diện tích hình chữ nhật tăng trên các khoảng \(\left( {0;\frac{\pi }{4}} \right)\) và \(\left( {\frac{{3\pi }}{4};\pi } \right)\), diện tích hình chữ nhật giảm trên khoảng \(\left( {\frac{\pi }{4};\frac{{3\pi }}{4}} \right)\).
- Giải bài 13 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 14 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 11 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 10 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 9 trang 11 sách bài tập toán 12 - Chân trời sáng tạo
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 12 - Chân trời sáng tạo - Xem ngay
Các bài khác cùng chuyên mục
- Giải bài 8 trang 37 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 7 trang 37 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 6 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 5 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 4 trang 36 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 7 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 6 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 5 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 4 trang 87 sách bài tập toán 12 - Chân trời sáng tạo
- Giải bài 3 trang 87 sách bài tập toán 12 - Chân trời sáng tạo












Danh sách bình luận