-
Đề khảo sát chất lượng đầu năm
-
Đề thi giữa kì 1 Toán 10
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 Toán 10 - Đề số 1
- Đề thi học kì 1 Toán 10 - Đề số 2
- Đề thi học kì 1 Toán 10 - Đề số 3
- Đề thi học kì 1 Toán 10 - Đề số 4
- Đề thi học kì 1 Toán 10 - Đề số 5
- Đề thi học kì 1 Toán 10 - Đề số 6
- Đề thi học kì 1 Toán 10 - Đề số 7
- Đề thi học kì 1 Toán 10 - Đề số 8
- Đề thi học kì 1 Toán 10 - Đề số 9
- Đề thi học kì 1 Toán 10 - Đề số 10
- Đề thi học kì 1 Toán 10 - Đề số 11
- Đề thi học kì 1 Toán 10 - Đề số 12
- Đề thi học kì 1 Toán 10 - Đề số 13
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề thi học kì 1 Toán 10 Cánh diều - Đề số 13
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
I. Phần trắc nghiệm
Đề bài
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
-
A.
\(\exists x \in \mathbb{R},{x^2} - x = 0\)
-
B.
\(\exists x \in \mathbb{R},x = {x^2}\)
-
C.
\(\forall x \in \mathbb{Z},{x^2} = x\)
-
D.
\(\exists x \in \mathbb{Z},x = {x^2}\)
Cho tập hợp \(A = \{ x \in \mathbb{R}| - 3 < x < 1\} \). Tập A là tập nào sau đây?
-
A.
{-3;1}
-
B.
[-3;1]
-
C.
[-3;1)
-
D.
(-3;1)
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(3x + 4y - 5 \le 0\)
-
B.
\(3x + {y^2} - 5 \le 0\)
-
C.
\({x^2} + y + 3 \le 0\)
-
D.
\(2xy - 5 \ge 0\)
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 5y - 1 > 0\\2x + y + 5 > 0\\x + y + 1 < 0\end{array} \right.\)?
-
A.
(0;0)
-
B.
(1;0)
-
C.
(0;-2)
-
D.
(0;2)
Cho tam giác ABC có \(A = {120^o}\) thì đẳng thức nào sau đây đúng?
-
A.
\({a^2} = {b^2} + {c^2} - 3bc\)
-
B.
\({a^2} = {b^2} + {c^2} + bc\)
-
C.
\({a^2} = {b^2} + {c^2} + 3bc\)
-
D.
\({a^2} = {b^2} + {c^2} - bc\)
Cho tam giác ABC. Tìm công thức đúng trong các công thức sau:
-
A.
\(S = \frac{1}{2}bc\sin A\)
-
B.
\(S = \frac{1}{2}ac\sin A\)
-
C.
\(S = \frac{1}{2}bc\sin B\)
-
D.
\(S = \frac{1}{2}bc\sin C\)
Cho hình bình hành ABCD. Vecto nào sau đây cùng phương với \(\overrightarrow {AB} \)?
-
A.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
B.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DA} \)
-
C.
\(\overrightarrow {AD} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
D.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {CB} \)
Biết \(\overrightarrow {AB} = \overrightarrow a \). Gọi C là điểm thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AB} \). Chọn khẳng định đúng.
-
A.
\(\overrightarrow {BC} = 2\overrightarrow a \)
-
B.
\(\overrightarrow {CA} = 2\overrightarrow a \)
-
C.
\(\overrightarrow {CB} = 2\overrightarrow a \)
-
D.
\(\overrightarrow {AC} = \overrightarrow 0 \)
Tập xác định của hàm số \(y = \sqrt {x + 2} - \sqrt {x + 3} \) là
-
A.
\(D = [ - 3; + \infty )\)
-
B.
\(D = [ - 2; + \infty )\)
-
C.
\(D = \mathbb{R}\)
-
D.
\(D = [2; + \infty )\)
Cho hai vecto \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \), \(\alpha \) là góc tạo vởi hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Chọn khẳng định đúng.
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
Parabol (P): \(y = 2{x^2} - 4x + 3\) có trục đối xứng là đường thẳng có phương trình là
-
A.
x = 2
-
B.
x = -1
-
C.
x = 1
-
D.
x = -2
Nghiệm của phương trình \(\sqrt {{x^2} + 3x - 2} = \sqrt {x + 1} \) là
-
A.
x = 1
-
B.
x = -3
-
C.
x = -3, x = 1
-
D.
\(x \in \emptyset \)
Một trò chơi ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ A thì người ấy được cộng 3 điểm, nếu chọn được chữ B thì bị 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi x, y theo thứ tự là số lần người chơi chọn được chữ A và chữ B.
a) Tổng số điểm người chơi đạt được khi chọn chữ A là 2x.
b) Tổng số điểm người chơi bị trừ khi chọn chữ B là y.
c) Bất phương trình bậc nhất hai ẩn x, y trong tình huống người chơi chiến thắng là \(3x - y \ge 18\).
d) Người chơi chọn được chữ A 8 lần và chọn được chữ B 3 lần thì người đó vừa đủ điểm để chiến thắng trò chơi.
Cho \(\sin \alpha = \frac{1}{2}\) với \({0^o} < \alpha < {90^o}\).
a) \(\cos \alpha < 0\).
b) \({\cos ^2}\alpha = \frac{5}{9}\).
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC.
a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Cho biểu thức \(f(x) = \frac{{x - 3}}{{{x^2} + 7x + 6}}\).
a) \(f(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 6\end{array} \right.\).
b) Với \(x \in ( - 6; - 1)\) thì \({x^2} + 7x + 6 < 0\).
c) Bảng xét dấu của biểu thức là:
d) Với \(x \in ( - \infty ; - 6) \cup ( - 1;3)\) thì f(x) > 0.
Cho hai tập hợp khác rỗng A = [0;5]; B = (2m;3m+1] đều khác tập rỗng. Có bao nhiêu giá trị nguyên m để \(A \cap B \ne \emptyset \)?
Đáp án:
Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng,
mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thế làm 40 giờ/tuần và tốn 6 giờ để làm một cái bàn, 3 giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp ba lần số bàn. Một cái bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Để lại thu về là lớn nhất, người thợ mộc phải sản xuất a cái bàn, b cái ghế trong c tuần. Hỏi a + b + c bằng bao nhiêu?
Đáp án:
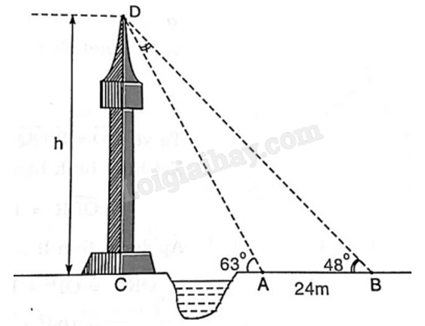
Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).
Đáp án:
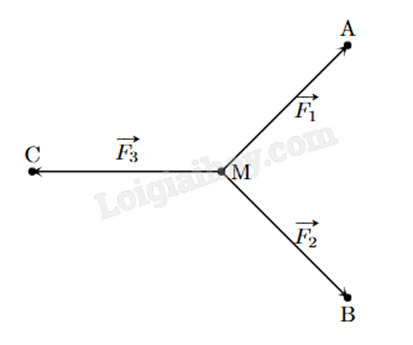
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án:
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
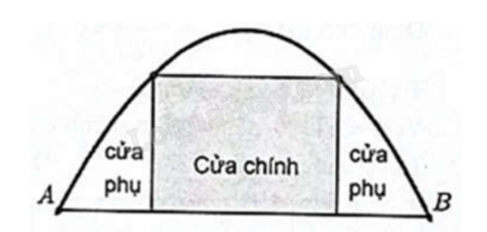
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn AB như hình vẽ).
Đáp án:
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách nhau sau: 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15080000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ?
Đáp án:
Lời giải và đáp án
Viết mệnh đề sau bằng kí hiệu \(\forall \) hoặc \(\exists \): “Có một số nguyên bằng bình phương của chính nó”.
-
A.
\(\exists x \in \mathbb{R},{x^2} - x = 0\)
-
B.
\(\exists x \in \mathbb{R},x = {x^2}\)
-
C.
\(\forall x \in \mathbb{Z},{x^2} = x\)
-
D.
\(\exists x \in \mathbb{Z},x = {x^2}\)
Đáp án : D
Đọc kĩ mệnh đề và áp dụng quy tắc sử dụng kí hiệu \(\forall \) và \(\exists \).
“Có một số nguyên” tức là tồn tại số nguyên: \(\exists x \in \mathbb{Z}\).
“Số (nguyên) bằng bình phương của chính nó”: \(x = {x^2}\).
Vậy mệnh đề đúng là “\(\exists x \in \mathbb{Z},x = {x^2}\)”.
Cho tập hợp \(A = \{ x \in \mathbb{R}| - 3 < x < 1\} \). Tập A là tập nào sau đây?
-
A.
{-3;1}
-
B.
[-3;1]
-
C.
[-3;1)
-
D.
(-3;1)
Đáp án : D
Với dấu “>” hoặc “<” ta dùng kí hiệu khoảng ().
\(x \in \mathbb{R}\) nên mọi số thực thỏa mãn -3 < x < 1 đều thuộc A. Tập {-3;1} chỉ có 2 giá trị nên A sai.
Với dấu “>” hoặc “<” ta dùng kí hiệu khoảng. Trong trường hợp này dùng kí hiệu nửa khoảng ở cả hai đầu mút.
Vậy A = (-3;1).
Bất phương trình nào sau đây là bất phương trình bậc nhất hai ẩn?
-
A.
\(3x + 4y - 5 \le 0\)
-
B.
\(3x + {y^2} - 5 \le 0\)
-
C.
\({x^2} + y + 3 \le 0\)
-
D.
\(2xy - 5 \ge 0\)
Đáp án : A
Quan sát dạng (ẩn, bậc) của bất phương trình.
Các bất phương trình ở đáp án B, C, D đều là bất phương trình bậc hai hai ẩn.
Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}2x - 5y - 1 > 0\\2x + y + 5 > 0\\x + y + 1 < 0\end{array} \right.\)?
-
A.
(0;0)
-
B.
(1;0)
-
C.
(0;-2)
-
D.
(0;2)
Đáp án : C
Thay tọa độ các điểm vào hệ phương trình, nếu thỏa mãn hệ điểm đó thuộc miền nghiệm.
Thay tọa độ các điểm vào hệ, chỉ có điểm (0;-2) thỏa mãn hệ.
Cho tam giác ABC có \(A = {120^o}\) thì đẳng thức nào sau đây đúng?
-
A.
\({a^2} = {b^2} + {c^2} - 3bc\)
-
B.
\({a^2} = {b^2} + {c^2} + bc\)
-
C.
\({a^2} = {b^2} + {c^2} + 3bc\)
-
D.
\({a^2} = {b^2} + {c^2} - bc\)
Đáp án : B
Sử dụng định lí Cosin cho tam giác.
\({a^2} = {b^2} + {c^2} - 2bc\cos A = {b^2} + {c^2} - 2bc\cos {120^o} = {b^2} + {c^2} - 2bc.\left( { - \frac{1}{2}} \right) = {b^2} + {c^2} + bc\).
Cho tam giác ABC. Tìm công thức đúng trong các công thức sau:
-
A.
\(S = \frac{1}{2}bc\sin A\)
-
B.
\(S = \frac{1}{2}ac\sin A\)
-
C.
\(S = \frac{1}{2}bc\sin B\)
-
D.
\(S = \frac{1}{2}bc\sin C\)
Đáp án : A
Áp dụng công thức tính diện tích tam giác.
\(S = \frac{1}{2}bc\sin A\).
Cho hình bình hành ABCD. Vecto nào sau đây cùng phương với \(\overrightarrow {AB} \)?
-
A.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
B.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {DA} \)
-
C.
\(\overrightarrow {AD} ,\overrightarrow {CD} ,\overrightarrow {DC} \)
-
D.
\(\overrightarrow {BA} ,\overrightarrow {CD} ,\overrightarrow {CB} \)
Đáp án : A
Các vecto cùng phương có giá song song với nhau.
Vì ABCD là hình bình hành nên AB // CD.
Khi đó \(\overrightarrow {AB} = \overrightarrow {BA} \), \(\overrightarrow {AB} = \overrightarrow {CD} \) và \(\overrightarrow {AB} = \overrightarrow {DC} \).
Biết \(\overrightarrow {AB} = \overrightarrow a \). Gọi C là điểm thỏa mãn \(\overrightarrow {CA} = \overrightarrow {AB} \). Chọn khẳng định đúng.
-
A.
\(\overrightarrow {BC} = 2\overrightarrow a \)
-
B.
\(\overrightarrow {CA} = 2\overrightarrow a \)
-
C.
\(\overrightarrow {CB} = 2\overrightarrow a \)
-
D.
\(\overrightarrow {AC} = \overrightarrow 0 \)
Đáp án : C
Dựng hình thỏa mãn đẳng thức trên và nhận xét.
Vì \(\overrightarrow {CA} = \overrightarrow {AB} \) nên hai vecto trên cùng phương và \(\overrightarrow {CA} ,\overrightarrow {AB} \) cùng chiều.
Khi đó A, B, C thẳng hàng và A nằm giữa B, C.
Vậy khẳng định đúng là \(\overrightarrow {CB} = 2\overrightarrow a \).
Tập xác định của hàm số \(y = \sqrt {x + 2} - \sqrt {x + 3} \) là
-
A.
\(D = [ - 3; + \infty )\)
-
B.
\(D = [ - 2; + \infty )\)
-
C.
\(D = \mathbb{R}\)
-
D.
\(D = [2; + \infty )\)
Đáp án : B
Biểu thức dưới dấu căn phải lớn hơn hoặc bằng 0.
Để hàm số trên xác định thì \(\left\{ \begin{array}{l}x + 2 \ge 0\\x + 3 \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \ge - 2\\x \ge - 3\end{array} \right.\)
Vậy \(D = [ - 2; + \infty )\).
Cho hai vecto \(\overrightarrow a \), \(\overrightarrow b \) khác \(\overrightarrow 0 \), \(\alpha \) là góc tạo vởi hai vecto \(\overrightarrow a \) và \(\overrightarrow b \) khi \(\overrightarrow a .\overrightarrow b = - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\). Chọn khẳng định đúng.
-
A.
\(\alpha = {180^o}\)
-
B.
\(\alpha = {0^o}\)
-
C.
\(\alpha = {90^o}\)
-
D.
\(\alpha = {45^o}\)
Đáp án : A
Áp dụng công thức tính tích vô hướng: \(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\).
\(\overrightarrow a .\overrightarrow b = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
\( \Rightarrow - \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right| = \left| {\overrightarrow a } \right|.\left| {\overrightarrow b } \right|\cos \alpha \)
\( \Rightarrow \cos \alpha = - 1\)
\( \Rightarrow \alpha = {180^o}\).
Parabol (P): \(y = 2{x^2} - 4x + 3\) có trục đối xứng là đường thẳng có phương trình là
-
A.
x = 2
-
B.
x = -1
-
C.
x = 1
-
D.
x = -2
Đáp án : C
Trục đối xứng của đồ thị hàm số có phương trình \(x = - \frac{b}{{2a}}\).
Trục đối xứng của đồ thị hàm số \(y = 2{x^2} - 4x + 3\) có phương trình \(x = - \frac{{ - 4}}{{2.2}} = 1\).
Nghiệm của phương trình \(\sqrt {{x^2} + 3x - 2} = \sqrt {x + 1} \) là
-
A.
x = 1
-
B.
x = -3
-
C.
x = -3, x = 1
-
D.
\(x \in \emptyset \)
Đáp án : A
\(\sqrt {f(x)} = \sqrt {g(x)} \Leftrightarrow \left\{ \begin{array}{l}f(x) = g(x)\\g(x) \ge 0\end{array} \right.\)
\(\sqrt {{x^2} + 3x - 2} = \sqrt {x + 1} \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 3x - 2 = x + 1\\x + 1 \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x^2} + 2x - 3 = 0\\x \ge 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\\x \ge 1\end{array} \right. \Leftrightarrow x = 1\).
Một trò chơi ô chữ đơn giản mà kết quả gồm một trong hai khả năng: Nếu người chơi chọn được chữ A thì người ấy được cộng 3 điểm, nếu chọn được chữ B thì bị 1 điểm. Người chơi chỉ chiến thắng khi đạt được số điểm tối thiểu là 20. Gọi x, y theo thứ tự là số lần người chơi chọn được chữ A và chữ B.
a) Tổng số điểm người chơi đạt được khi chọn chữ A là 2x.
b) Tổng số điểm người chơi bị trừ khi chọn chữ B là y.
c) Bất phương trình bậc nhất hai ẩn x, y trong tình huống người chơi chiến thắng là \(3x - y \ge 18\).
d) Người chơi chọn được chữ A 8 lần và chọn được chữ B 3 lần thì người đó vừa đủ điểm để chiến thắng trò chơi.
a) Tổng số điểm người chơi đạt được khi chọn chữ A là 2x.
b) Tổng số điểm người chơi bị trừ khi chọn chữ B là y.
c) Bất phương trình bậc nhất hai ẩn x, y trong tình huống người chơi chiến thắng là \(3x - y \ge 18\).
d) Người chơi chọn được chữ A 8 lần và chọn được chữ B 3 lần thì người đó vừa đủ điểm để chiến thắng trò chơi.
Ứng dụng bất phương trình bậc nhất hai ẩn để giải.
a) Sai. Vì mỗi lần chọn được chữ A thì được cộng 3 điểm nên sau x lần chọn chữ A, người chơi được 3x điểm.
b) Đúng. Vì mỗi lần chọn được chữ B thì bì trừ 1 điểm nên sau y lần chọn chữ B, người chơi bị trừ y điểm.
c) Sai. Người chơi cần ít nhất 20 điểm để chiến thắng trò chơi nên \(3x - y \ge 20\).
d) Sai. Thay cặp số (8;3) vào bất phương trình được \(3.8 - 1.3 = 21 > 20\).
Vậy người chơi thừa 1 điểm so với điểm tối thiểu để chiến thắng trò chơi.
Cho \(\sin \alpha = \frac{1}{2}\) với \({0^o} < \alpha < {90^o}\).
a) \(\cos \alpha < 0\).
b) \({\cos ^2}\alpha = \frac{5}{9}\).
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
a) \(\cos \alpha < 0\).
b) \({\cos ^2}\alpha = \frac{5}{9}\).
c) \(\cos ({180^o} - \alpha ) = - \frac{1}{3}\).
d) Giá trị biểu thức \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Sử dụng kiến thức về dấu của các giá trị lượng giác của các góc.
Áp dụng công thức \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\), \(\cos ({180^o} - \alpha ) = - \cos \alpha \).
a) Sai. Có \({0^o} < \alpha < {90^o}\) suy ra \(\cos \alpha > 0\).
b) Sai. \({\cos ^2}\alpha = 1 - {\sin ^2}\alpha = 1 - {\left( {\frac{1}{3}} \right)^2} = \frac{8}{9}\).
c) Sai. Vì \(\cos \alpha > 0\) nên \(\cos \alpha = \sqrt {\frac{8}{9}} = \frac{{2\sqrt 2 }}{3}\).
\(\cos ({180^o} - \alpha ) = - \cos \alpha = - \frac{{2\sqrt 2 }}{3}\).
d) Đúng. Ta có: \(P = \frac{{\sin \alpha + \cos \alpha }}{{2\sin \alpha + \cos \alpha }} = \frac{{\frac{1}{3} + \frac{{2\sqrt 2 }}{3}}}{{2.\frac{1}{3} + \frac{{2\sqrt 2 }}{3}}} = \frac{{1 + 2\sqrt 2 }}{{2 + 2\sqrt 2 }}\).
Cho tam giác ABC có G là trọng tâm. Gọi D là điểm đối xứng của B qua G và M là trung điểm của BC.
a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
a) \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
b) \(\overrightarrow {AG} = 2\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) \(\overrightarrow {CD} = \overrightarrow {AB} - \overrightarrow {AC} + \frac{1}{3}\overrightarrow {BG} \).
d) \(\overrightarrow {MD} = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Áp dụng quy tắc ba điểm, quy tắc hình bình hành, tính chất trung điểm đối với vecto, quy tắc cộng, trừ hai vecto.
a) Đúng. Theo quy tắc ba điểm: \(\overrightarrow {MG} = \overrightarrow {MG} + \overrightarrow {GD} \).
b) Sai. \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AM} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{1}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \).
c) Sai. \(\overrightarrow {CD} = \overrightarrow {CB} + \overrightarrow {BD} = \overrightarrow {AB} - \overrightarrow {AC} + 2\overrightarrow {BG} \).
d) Đúng. \(\overrightarrow {MD} = \overrightarrow {MG} + \overrightarrow {GD} = - \frac{1}{3}\overrightarrow {AM} + \overrightarrow {BG} = - \frac{1}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) + \left( {\overrightarrow {BA} + \frac{2}{3}\overrightarrow {AM} } \right)\)
\( = - \frac{1}{6}\overrightarrow {AB} - \frac{1}{6}\overrightarrow {AC} - \overrightarrow {AB} + \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = - \frac{5}{6}\overrightarrow {AB} + \frac{1}{6}\overrightarrow {AC} \).
Cho biểu thức \(f(x) = \frac{{x - 3}}{{{x^2} + 7x + 6}}\).
a) \(f(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 6\end{array} \right.\).
b) Với \(x \in ( - 6; - 1)\) thì \({x^2} + 7x + 6 < 0\).
c) Bảng xét dấu của biểu thức là:
d) Với \(x \in ( - \infty ; - 6) \cup ( - 1;3)\) thì f(x) > 0.
a) \(f(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 6\end{array} \right.\).
b) Với \(x \in ( - 6; - 1)\) thì \({x^2} + 7x + 6 < 0\).
c) Bảng xét dấu của biểu thức là:
d) Với \(x \in ( - \infty ; - 6) \cup ( - 1;3)\) thì f(x) > 0.
Tìm nghiệm và các giá trị x để f(x) không xác định. Từ đó lập bảng xét dấu và nhận xét.
a) Sai. \(f(x) = \frac{{x - 3}}{{{x^2} + 7x + 6}} = 0 \Leftrightarrow x - 3 = 0 \Leftrightarrow x = 3\).
b) Đúng. \({x^2} + 7x + 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 1\\x = - 6\end{array} \right.\)
Áp dụng quy tắc “Trong trái, ngoài cùng”, tức trong khoảng hai nghiệm thì f(x) trái dấu với a = 1 > 0.
Vậy với \(x \in ( - 6; - 1)\) thì \({x^2} + 7x + 6 < 0\).
c) Đúng. Bảng xét dấu đã cho là chính xác.
d) Sai. Với \(x \in ( - \infty ; - 6) \cup ( - 1;3)\) thì f(x) < 0.
Cho hai tập hợp khác rỗng A = [0;5]; B = (2m;3m+1] đều khác tập rỗng. Có bao nhiêu giá trị nguyên m để \(A \cap B \ne \emptyset \)?
Đáp án:
Đáp án:
Tìm điều kiện để \(A \cap B = \emptyset \), từ đó suy ra điều kiện để \(A \cap B \ne \emptyset \) bằng cách lấy phần bù.
\(B \ne \emptyset \) khi \(2m < 3m + 1 \Rightarrow m > - 1\).
Ta có \(A \cap B = \emptyset \Leftrightarrow \left[ \begin{array}{l}\left\{ \begin{array}{l}2m \ge 5\\3m + 1 < 0\end{array} \right.\\m > - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m \ge \frac{5}{2}\\ - 1 < m < - \frac{1}{3}\end{array} \right.\)
Suy ra \(A \cap B \ne \emptyset \Leftrightarrow m \in \left[ { - \frac{1}{3};\frac{5}{2}} \right)\).
Các giá trị nguyên m thỏa mãn là 0; 1; 2.
Vậy có 3 giá trị nguyên m thỏa mãn yêu cầu đề bài.
Một người thợ mộc làm những cái bàn và những cái ghế. Mỗi cái bàn khi bán lãi 150 nghìn đồng,
mỗi cái ghế khi bán lãi 50 nghìn đồng. Người thợ mộc có thế làm 40 giờ/tuần và tốn 6 giờ để làm một cái bàn, 3 giờ để làm một cái ghế. Khách hàng yêu cầu người thợ mộc làm số ghế ít nhất là gấp ba lần số bàn. Một cái bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần. Để lại thu về là lớn nhất, người thợ mộc phải sản xuất a cái bàn, b cái ghế trong c tuần. Hỏi a + b + c bằng bao nhiêu?
Đáp án:
Đáp án:
Ứng dụng hệ bất phương trình bậc nhất hai ẩn.
Gọi x và y lần lượt là số bàn và số ghế mà người thợ mộc sản xuất trong một tuần \((x,y \ge 0)\).
Để làm x cái bàn cần 6x (giờ), làm y cái ghế cần 3y (giờ). Người thợ mộc chỉ có thể làm 40 giờ/tuần nên \(6x + 3y \le 40\).
Số ghế gấp ít nhất ba lần số bàn nên \(y \ge 3x\).
Một cái bàn chiếm chỗ bằng 4 cái ghế và ta có phòng để được nhiều nhất 4 cái bàn/tuần nên \(x + \frac{4}{y} \le 4\).
Ta có hệ bất phương trình \(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\x + \frac{y}{4} \le 4\\x,y \ge 0\end{array} \right.\) hay \(\left\{ \begin{array}{l}6x + 3y \le 40\\y \ge 3x\\4x + y \le 16\\x,y \ge 0\end{array} \right.\) (*).
Lợi nhuận thu được là f(x;y) = 150x + 50y (nghìn đồng).
Bài toán trở thành tìm giá trị lớn nhất của f(x;y) trên miền nghiệm của hệ (*).
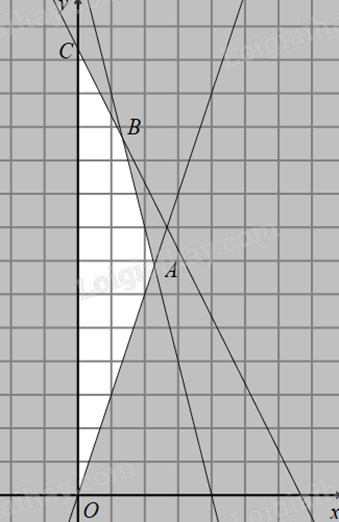
Miền nghiệm của hệ (*) là miền tứ giác OABC (kể cả biên) với \(A\left( {\frac{{16}}{7};\frac{{48}}{7}} \right)\), \(B\left( {\frac{4}{3};\frac{{32}}{2}} \right)\), \(C\left( {0;\frac{{40}}{3}} \right)\).
Thay tọa độ các điểm trên vào f(x;y) thấy \(f\left( {\frac{4}{3};\frac{{32}}{3}} \right) = \frac{{2200}}{3}\) là giá trị lớn nhất.
Như vậy người thợ này cần sản xuất 4 cái bàn và 32 cái ghế trong vòng 3 tuần để thu về số tiên lãi lớn nhất.
Ta có a + b + c = 4 + 32 + 3 = 39.
Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).
Đáp án:
Đáp án:
B1: Tính các góc của tam giác ABD.
B2: Tính AD bằng định lí Sin cho tam giác ABD.
B3: Sử dụng hệ thức lượng trong tam giác vuông CAD để tính CD.
+) \(\widehat {CAD} + \widehat {BAD} = {180^o} \Rightarrow \widehat {BAD} = {180^o} - \widehat {CAD} = {180^o} - {63^o} = {117^o}\).
+) Xét tam giác ABD có \(\widehat D = {180^o} - \widehat A - \widehat B = {180^o} - {117^o} - {48^o} = {15^o}\).
Áp dụng định lí Sin cho tam giác ABD: \(\frac{{AB}}{{\sin \widehat {BDA}}} = \frac{{AD}}{{\sin \widehat {ABD}}}\).
Suy ra \(AD = \frac{{AB\sin \widehat {ABD}}}{{\sin \widehat {ADB}}} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\).
Xét tam giác ACD vuông tại C: \(\sin \widehat {CAD} = \frac{{CD}}{{AD}}\).
Suy ra \(CD = AD\sin \widehat {CAD} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\sin {63^o} \approx 61,4\) (m).
Cho ba lực \(\overrightarrow {{F_1}} = \overrightarrow {MA} \), \(\overrightarrow {{F_2}} = \overrightarrow {MB} \), \(\overrightarrow {{F_3}} = \overrightarrow {MC} \) cùng tác động vào một vật tại điểm M và vật đứng yên. Cho biết cường độ của \(\overrightarrow {{F_1}} \), \(\overrightarrow {{F_2}} \) đều bằng 100 N và góc \(\widehat {AMB} = {90^o}\). Tính cường độ của lực \(\overrightarrow {{F_3}} \) (làm tròn đến hàng đơn vị).
Đáp án:
Đáp án:
Sử dụng quy tắc tổng hợp lực, quy tắc hình bình hành.
Dựng hình bình hành AMBD. Vì \(\widehat {AMB} = {90^o}\) nên AMBD là hình vuông.
Áp dụng quy tắc hình bình hành, ta có \(\overrightarrow {MA} + \overrightarrow {MB} = \overrightarrow {MD} \).
Vì vật đứng yên nên \(\overrightarrow {MA} + \overrightarrow {MB} + \overrightarrow {MC} = \overrightarrow 0 \).
Từ đó ta suy ra \(\overrightarrow {MD} + \overrightarrow {MC} = \overrightarrow 0 \) hay \(\overrightarrow {MD} = - \overrightarrow {MC} \). Khi đó \(\left| {\overrightarrow {MD} } \right| = \left| { - \overrightarrow {MC} } \right|\) tức MD = MC.
Vì MD là đường chéo của hình vuông cạnh 100 nên \(MD = 100\sqrt 2 \).
Vậy \(\left| {\overrightarrow {{F_3}} } \right| = \left| {\overrightarrow {MC} } \right| = 100\sqrt 2 \approx 141\) N.
Một chiếc cổng hình parabol bao gồm một cửa chính hình chữ nhật ở giữa và hai cánh cửa phụ hai bên như hình vẽ.
Biết chiều cao cổng parabol là 4 m, cửa chính (ở giữa parabol) cao 3 m và rộng 4 m. Tính khoảng cách giữa hai chân cổng parabol ấy (đoạn AB như hình vẽ).
Đáp án:
Đáp án:
Dựng hệ trục Oxy một cách phù hợp.
Thay tọa độ các điểm thuộc parabol vào hàm số \(y = a{x^2} + bx + c\) rồi tính hệ số a, b, c.
Tìm giao điểm của parabol với trục Ox và tính khoảng cách giữa hai giao điểm đó.
Dựng hệ trục Oxy như hình vẽ.
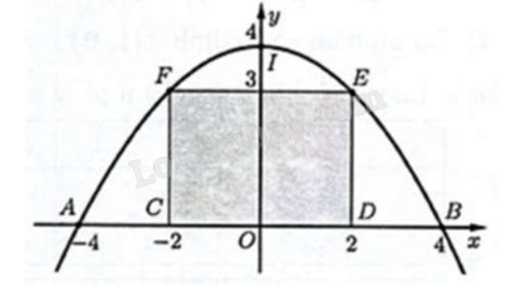
Gọi (P): \(y = a{x^2} + bx + c\) \((a \ne 0)\).
Ta có (P) đi qua các điểm I(0;4), E(2;3), F(-2;3) nên \(\left\{ \begin{array}{l}c = 4\\4a + 2b + c = 3\\4a - 2b + c = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{4}\\b = 0\\c = 4\end{array} \right.\).
Từ đó suy ra (P): \(y = - \frac{1}{4}{x^2} + 4\).
Hai điểm A, B là giao điểm của (P) với trục Ox nên hoành độ thỏa mãn \( - \frac{1}{4}{x^2} + 4 = 0 \Leftrightarrow x = \pm 4\).
Do đó A(-4;0) và B(4;0). Suy ra AB = 8.
Một công ty du lịch thông báo giá tiền cho chuyến đi tham quan của một nhóm khách nhau sau: 50 khách đầu tiên có giá 300000 đồng/người. Nếu có nhiều hơn 50 người đăng kí thì cứ có thêm 1 người, giá vé sẽ giảm 5000 đồng/người cho toàn bộ hành khách. Biết chi phí thực sự của chuyến đi là 15080000 đồng. Số người của nhóm khách du lịch nhiều nhất là bao nhiêu để công ty không bị lỗ?
Đáp án:
Đáp án:
Lập tam thức bậc hai biểu diễn số tiền vé thu được.
Sử dụng định lí về dấu của tam thức bậc hai để tìm khoảng mà tam thức bậc hai vừa tìm không âm.
Với số khách là 50, công ty thu về 50.300000 = 15000000 (đồng), ít hơn chi phí thực sự nên công ty lỗ.
Vì vậy, số khách phải lớn hơn 50 để công ty không lỗ.
Với số lượng khách là 50 + x thì mỗi khách sẽ trả một khoản tiền là 300000 – 5000x (đồng).
Khi đó, tổng số tiền công ty thu được là:
\(T(x) = (50 + x)(300000 - 5000x) = - 5000{x^2} + 50000x + 15000000\) (đồng).
f(x) có hai nghiệm phân biệt là 2 và 8. Ta có bảng xét dấu:
Từ bảng xét dấu, ta suy ra \(f(x) \ge 0\) khi \(x \in [2;8]\).
Vậy, nếu số khách tối đa là 58 người thì công ty không lỗ khi tổ chức chuyến du lịch.
I. Phần trắc nghiệm
I. Phần trắc nghiệm
Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề? a) Huế là một thành phố của Việt Nam. b) Sông Hương chảy ngang qua thành phố Huế. c) Hãy trả lời câu hỏi này! d) (5 + 19 = 24.) e) (6 + 81 = 25.) f) Bạn có mang theo máy tính không? g) (x + 2 = 11.)
Câu 1: Tìm tập xác định ({rm{D}}) của hàm số (y = sqrt {6 - 3x} + frac{1}{{sqrt {x - 1} }}.) A. ({rm{D}} = left[ {1;2} right].) B. ({rm{D}} = left( {1;2} right).) C. ({rm{D}} = (1;2].) D. ({rm{D}} = left[ { - 1;2} right].)
Câu 1: Trong các câu sau, có bao nhiêu câu là mệnh đề? a) Hãy đi nhanh lên! b) Hà Nội là thủ đô của Việt Nam. c) (5 + 7 + 4 = 15) d) Năm 2018 là năm nhuận.
Câu 1: Cho các phát biểu sau đây: (1) “17 là số nguyên tố”. (2) “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”. (3) “Các em C14 hãy cố gắng học tập thật tốt nhé!” (4) “Mọi hình chữ nhật đều nội tiếp được đường tròn”. Hỏi có bao nhiêu phát biểu là mệnh đề?
Câu 1: Tìm tập xác định \({\rm{D}}\) của hàm số \(y = \sqrt {6 - 3x} - \sqrt {x - 1} .\) A. \({\rm{D}} = \left[ {1;2} \right].\) B. \({\rm{D}} = \left( {1;2} \right).\) C. \({\rm{D}} = \left[ {1;3} \right].\) D. \({\rm{D}} = \left[ { - 1;2} \right].\)
Câu 1: (ID: 592114) Câu nào sau đây không phải là mệnh đề? A. Bạn bao nhiêu tuổi? B. Hôm nay là chủ nhật. C. Trái đất hình tròn. D. \(4 \ne 5\)
Câu 1: Cho mệnh đề chứa biến với(x) là số thực. Mệnh đề nào sau đây là đúng: A. (Pleft( 3 right)). B. (Pleft( 4 right)). C. (Pleft( 1 right)). D. (Pleft( 5 right)).
Câu 1: Cho đồ thị hàm số \(y = {x^3}\) như hình bên: Khẳng định nào sau đây sai? A. Hàm số đồng biến trên khoảng \(\left( { - \infty ;0} \right)\). B. Hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\). C. Hàm số đồng biến trên khoảng \(\left( { - \infty ; + \infty } \right)\). D. Hàm số đồng biến tại gốc tọa độ O.
Câu 1: Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - 4y + 12 \ge 0}\\{x + y - 5 \ge 0}\\{x + 1 > 0}\end{array}} \right.\)là miền chứa điểm nào trong các điểm sau?
Câu 1: Tập \(S = \left\{ {\left. {q \in \mathbb{Q}} \right|25{q^4} - 9{q^2} = 0} \right\}\) có bao nhiêu phần tử?
A. Nội dung ôn tập Mệnh đề và tập hợp 1. Mệnh đề toán học 2. Tập hợp. Các phép toán trên tập hợp Bất phương trình và hệ bất phương trình bậc nhất hai ẩn 1. Bất phương trình bậc nhất hai ẩn 2. Hệ bất phương trình bậc nhất hai ẩn
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
