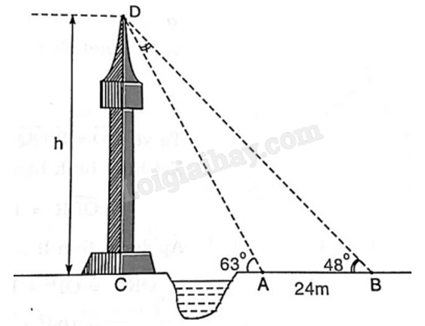
Muốn đo chiều cao CD của một cái tháp mà ta không thể đến được tâm C của chân tháp. Trong mặt phẳng đứng chứa chiều cao CD của tháp ta chọn hai điểm A và B sao cho ba điểm A, B, C thẳng hàng. Giả sử ta đo được khoảng cách AB = 24 m và các góc \(\widehat {CAD} = {63^o}\), \(\widehat {CBD} = {48^o}\). Hãy tính chiều cao h = CD của tháp (kết quả làm tròn đến hàng phần mười).
Đáp án:
Đáp án:
B1: Tính các góc của tam giác ABD.
B2: Tính AD bằng định lí Sin cho tam giác ABD.
B3: Sử dụng hệ thức lượng trong tam giác vuông CAD để tính CD.
+) \(\widehat {CAD} + \widehat {BAD} = {180^o} \Rightarrow \widehat {BAD} = {180^o} - \widehat {CAD} = {180^o} - {63^o} = {117^o}\).
+) Xét tam giác ABD có \(\widehat D = {180^o} - \widehat A - \widehat B = {180^o} - {117^o} - {48^o} = {15^o}\).
Áp dụng định lí Sin cho tam giác ABD: \(\frac{{AB}}{{\sin \widehat {BDA}}} = \frac{{AD}}{{\sin \widehat {ABD}}}\).
Suy ra \(AD = \frac{{AB\sin \widehat {ABD}}}{{\sin \widehat {ADB}}} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\).
Xét tam giác ACD vuông tại C: \(\sin \widehat {CAD} = \frac{{CD}}{{AD}}\).
Suy ra \(CD = AD\sin \widehat {CAD} = \frac{{24\sin {{48}^o}}}{{\sin {{15}^o}}}\sin {63^o} \approx 61,4\) (m).

Các bài tập cùng chuyên đề
Từ một khu vực có thể quan sát được hai đỉnh núi, ta có thể ngắm và đo để xác định khoảng cách giữa hai đỉnh núi đó. Hãy thảo luận để đưa ra các bước cho một cách đo.
Giải tam giác ABC, biết b = 32, c =45, \(\widehat A = {87^o}\)
a) Tính các góc của tam giác ABC.
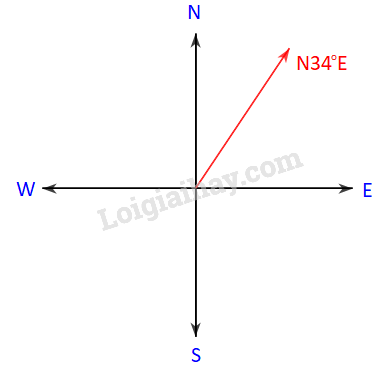
Trên biển, tàu B ở vị trí cách tàu A 53km về hướng \(N{34^o}E\). Sau đó, tàu B chuyển động thẳng đều với vận tốc có độ lớn 30 km/h về hướng đông, đồng thời tàu A chuyển động thẳng đều với vận tốc có độ lớn 50 km/h để gặp tàu B.
a) Hỏi tàu A cần phải chuyển động theo hướng nào?
b) Với hướng chuyển động đó thì sau bao lâu tàu A gặp tàu B?
Ngắm Tháp Rùa từ bờ, chỉ với những dụng cụ đơn giản, dễ chuẩn bị, ta cũng có thể xác định được khoảng cách từ vị trí đứng tới tháp rùa. Em có biết vì sao không?
Viết công thức định lí sin cho tam giác ABC.
Cho tam giác ABC có \(AB = c, Ac = b, BC = a\). Viết công thức tính cos A.
Cho tam giác ABC có \(AB = c, AC = b, \widehat A = \alpha \). Viết công thức tính BC theo \(b,c,\alpha \)
Từ trên nóc của một tòa nhà cao 18,5 m, bạn Nam quan sát một cái cây cách tòa nhà 30 m và dùng giác kế đo được góc lệch giữa phương quan sát gốc cây và phương nằm ngang là \({34^o}\), góc lệch giữa phương quan sát ngọn cây và phương nằm ngang là \({24^o}\). Biết chiều cao của chân giác kế là 1,5 m. Chiều cao của cái cây là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Từ xa xưa, con người đã cần đo đạc các khoảng cách mà không thể trực tiếp đo được. Chẳng hạn, để đo khoảng cách từ vị trí A trên bờ biển tới một hòn đảo (hay con tàu,...) trên biển, người xưa đã tìm ra một cách đo khoảng cách đó như sau:
Từ vị trí A, đo góc nghiêng \(\alpha\) so với bờ biển tới một vị trí C quan sát được trên đảo. Sau đó di chuyển dọc bờ biển đến vị trí B cách A một khoảng d và tiếp tục đo góc nghiêng \(\beta\) so với bờ biển tới vị trí C đã chọn (Hình 18).
Bằng cách giải tam giác ABC,họ tính được khoảng cách AC.
Giải tam giác được hiểu như thế nào?

Giải tam giác ABC trong các trường hợp sau:
a) \(a = 17,4;\widehat B = {44^o}30';\widehat C = {64^o}.\)
b) \(a = 10;b = 6;c = 8.\)
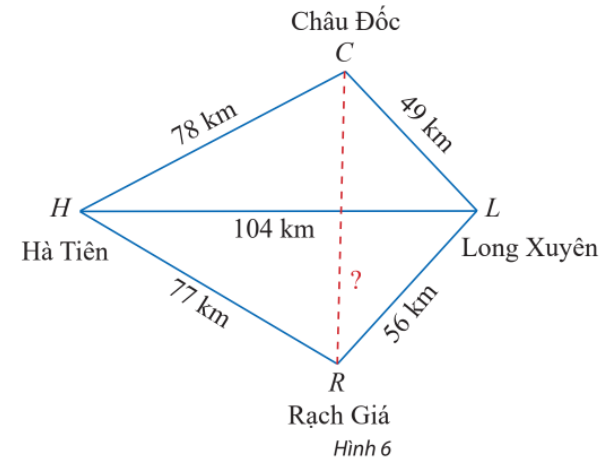
Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.
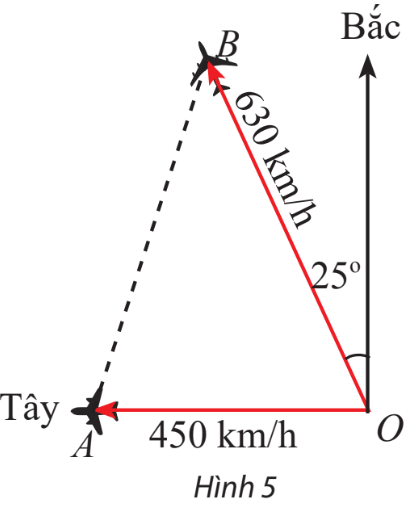
Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc \({25^o}\) về phía tây với tốc độ 630 km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.
d) \(AB = 23,AC = 32,BC = 44\)
c) \(AC = 22,\widehat B = {120^o},\widehat C = {28^o}.\)
b) \(BC = 22,4;\widehat B = {64^o};\widehat C = {38^o}.\)
a) \(AB = 14,AC = 23,\widehat A = {125^o}.\)
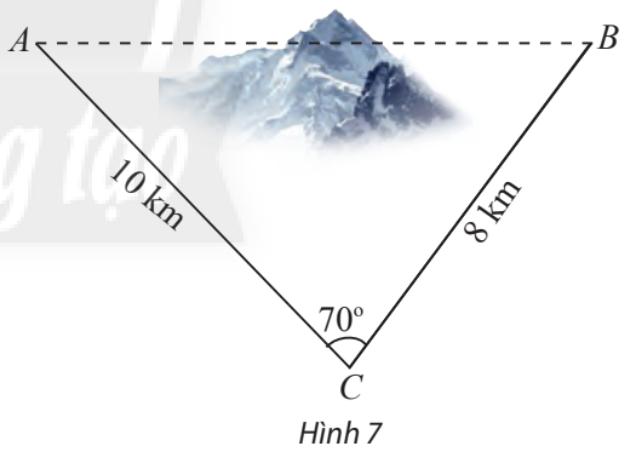
Để lắp đường dây diện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là \({70^o}\). Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B.
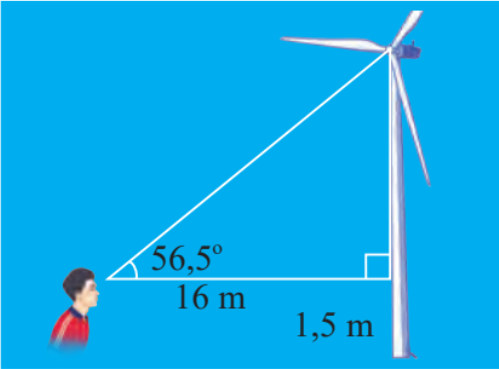
Một người đứng cách thân một các quạt gió 16 m và nhìn thấy tâm của cánh quạt với góc nâng \(56,{5^o}\) (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 1,5m.
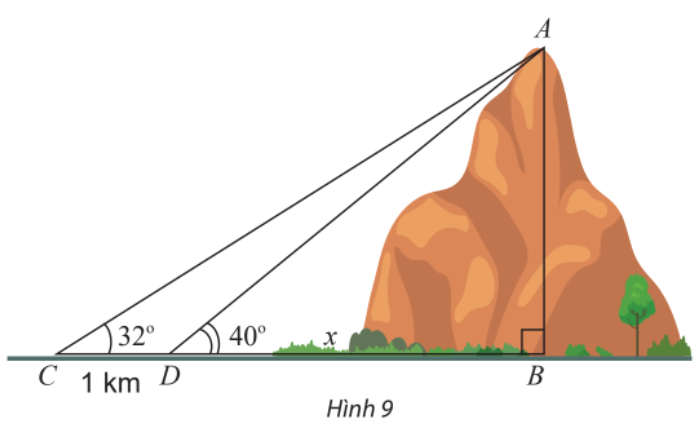
Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là \({32^ \circ }\) và \({40^ \circ }\) (Hình 9).
Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng \({32^ \circ }\) so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là \({62^ \circ }\). Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu đó là \({70^ \circ }\). Tính khoảng cách từ Q đến khinh khí cầu.
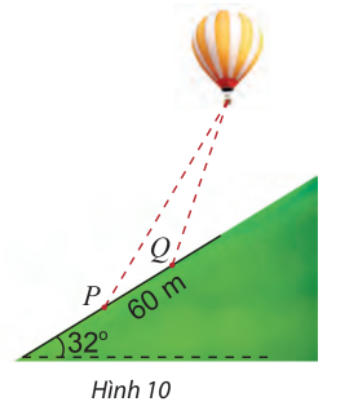
Hai người quan sát khinh khí cầu tại hai địa điểm P và Q nằm ở sườn đồi nghiêng \({32^ \circ }\) so với phương ngang, cách nhau 60 m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là \({62^ \circ }\). Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu đó là \({70^ \circ }\). Tính khoảng cách từ Q đến khinh khí cầu.

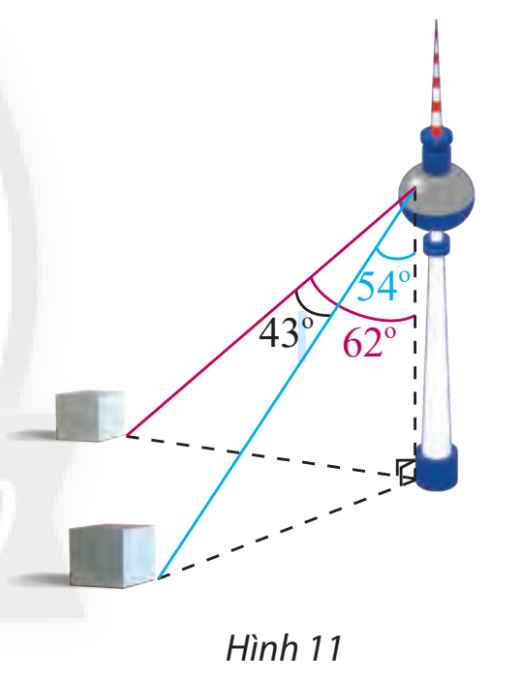
Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt dất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là \({43^ \circ }\), góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là \({62^ \circ }\) và đến điểm mốc khác là \({54^ \circ }\)(Hình 11). Tính khoảng cách giữa hai cột mốc này.
Cho tam giác ABC. Biết \(a = 49,4;b = 26,4;\widehat C = {47^ \circ }20'.\) Tính hai góc \(\widehat A,\widehat B\) và cạnh c.
Cho tam giác ABC. Biết \(a = 24,b = 13,c = 15.\) Tính các góc \(\widehat A,\widehat B,\widehat C.\)
a) Tam giác ABC có góc tù không?
a) Cạnh a và các góc \(\widehat B,\widehat C.\)
Cho tam giác MNP vuông tại M, NP = 16 và \(\widehat {PNM} = {30^o}\). Tính độ dài cạnh MP.
-
A.
\(8\sqrt 3 \)
-
B.
8
-
C.
32
-
D.
16
Một tàu các xuất phát từ đảo \(A,\) chạy 50 km theo hướng \(N{24^ \circ }E\) đến đảo \(B\) để lấy thêm ngư cụ, rồi chuyển hướng \(N{36^ \circ }W\) chạy tiếp 130 km đến ngư trường \(C.\)
a) Tính khoảng cách từ vị trí xuất phát từ A đến C (làm tròn đến hàng đơn vị, theo đơn vị đo ki lô mét).
b) Tìm hướng từ A đến C ( đơn vị đến hàng đơn vị, theo đơn vị độ).








Danh sách bình luận