 Đề thi toán 10, đề kiểm tra toán 10 cánh diều có đáp án và lời giải chi tiết
Đề thi toán 10, đề kiểm tra toán 10 cánh diều có đáp án và lời giải chi tiết
 Đề thi học kì 1 Toán 10 - Cánh diều
Đề thi học kì 1 Toán 10 - Cánh diều Đề thi học kì 1 Toán 10 Cánh diều - Đề số 7
Câu 1: Cho các phát biểu sau đây: (1) “17 là số nguyên tố”. (2) “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”. (3) “Các em C14 hãy cố gắng học tập thật tốt nhé!” (4) “Mọi hình chữ nhật đều nội tiếp được đường tròn”. Hỏi có bao nhiêu phát biểu là mệnh đề?
Đề bài
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
Câu 1: (ID: 592095) Cho các phát biểu sau đây:
(1) “17 là số nguyên tố”.
(2) “Tam giác vuông có một đường trung tuyến bằng nửa cạnh huyền”.
(3) “Các em C14 hãy cố gắng học tập thật tốt nhé!”
(4) “Mọi hình chữ nhật đều nội tiếp được đường tròn”.
Hỏi có bao nhiêu phát biểu là mệnh đề?
A. 4. B. 3. C. 2. D. 1.
Câu 2: (ID: 592097) Cho tam giác ABC có trung tuyến AM. Đặt \(\vec a{\rm{ \;}} = \overrightarrow {AB} ,{\mkern 1mu} {\mkern 1mu} \vec b{\rm{ \;}} = \overrightarrow {AM} \). Giả sử \(\overrightarrow {AC} {\rm{ \;}} = x\vec a{\rm{ \;}} + y\vec b,{\mkern 1mu} {\mkern 1mu} ,x,{\mkern 1mu} {\mkern 1mu} y \in \mathbb{R}\). Tìm cặp số (x;y) tương ứng.
A. (-1;-2). B. (1;2). C. (-1;2). D. (1;-2).
Câu 3: (ID: 592098) Lớp 10A có 37 học sinh, trong đó có 17 học sinh thích môn Văn, 19 học sinh thích môn Toán, 9 em không thích môn Văn và Toán. Số học sinh tích cả hai môn Văn và Toán là:
A. 13. B. 8. C. 6. D. 2.
Câu 4: (ID: 592099) Tìm tập nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x - 4 \ge 0}\\{\frac{{x - 1}}{2} - x \ge {\rm{ \;}} - 2}\end{array}} \right.\).
A. \(S = \left[ {3; + \infty } \right).\) B. \(S = \left[ {\frac{4}{3};3} \right].\) C. \(S = \left[ {\frac{4}{3}; + \infty } \right).\) D. \(S = \emptyset .\)
Câu 5: (ID: 592100) Miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + y - 1 > 0}\\{y \ge 2}\\{ - x + 2y > 3}\end{array}} \right.\) là phần không tô đậm của hình vẽ nào trong các hình vẽ sau:
A. 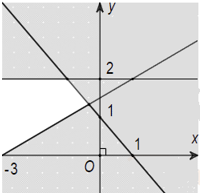 B.
B. 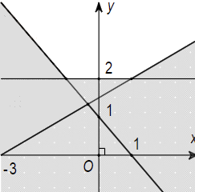 C.
C. 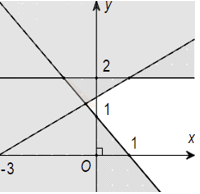 D.
D. 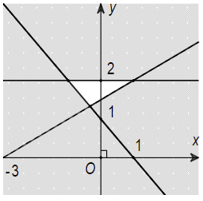
Câu 6: (ID: 592101) Cho tam giác ABC có AB = 9, AC = 18 và A = 600. Bán kính R của đường tròn ngoại tiếp tam giác ABC là:
A. 3. B. \(9\sqrt 3 .\) C. 9. D. 6.
Câu 7: (ID: 592102) Một người ngồi trên tàu hỏa đi từ ga A đến ga B. Khi đỗ tàu ở ga A, qua ống nhòm người đó nhìn thấy một tháp C. Hướng nhìn từ người đó đến tháp tạo với hướng đi của tàu một góc 600. Khi tàu đỗ ở ga B, người đó nhìn lại vẫn thấy tháp C, hướng nhìn từ người đó đến tháp tạo với hướng ngược với hướng đi của tàu một góc 450. Biết rằng đoạn đường tàu nối thẳng ga A với ga B dài 8km. Hỏi khoảng cách từ ga A đến tháp C gần nhất với số nào sau đây?

A. 5,9. B. 5,86. C. 5,78. D. 5,8.
Câu 8: (ID: 592103) Biểu thức \({\tan ^2}x{\sin ^2}x - {\tan ^2}x + {\sin ^2}x\) có giá trị bằng
A. -1. B. 0. C. 2. D. 1.
Câu 9: (ID: 592104) Gọi AN, CM là các đường trung tuyến của tam giác ABC. Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {AB} {\rm{ \;}} = \frac{2}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{2}{3}\overrightarrow {CM} \). B. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} - \frac{2}{3}\overrightarrow {CM} \). C. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{4}{3}\overrightarrow {CM} \). D. \(\overrightarrow {AB} {\rm{ \;}} = \frac{4}{3}\overrightarrow {AN} {\rm{ \;}} + \frac{2}{3}\overrightarrow {CM} \).
Câu 10: (ID: 592105) Gọi G là trọng tâm của tam giác ABC, nếu điểm M thỏa mãn hệ thức \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + 4\overrightarrow {MC} {\rm{ \;}} = \vec 0\) thì vị trí của điểm M thuộc miền nào trong hình vẽ?
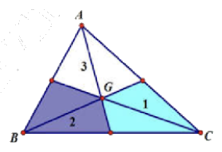
A. Miền 1. B. Miền 2. C. Miền 3. D. ở ngoài tam giác ABC.
Câu 11: Tập xác định của hàm số \(y = \frac{{\sqrt {2x + 1} }}{{3 - x}}\) là:
A. \(D = \left( {3; + \infty } \right)\). B. \(D = \left( { - \infty ;3} \right)\). C. \(D = \left[ { - \frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}\). D. \(D = \mathbb{R}\).
Câu 12: (ID: 592107) Trong tam giác ABC, hệ thức nào sau đây sai?
A. \(a = \frac{{b\sin A}}{{\sin B}}.\) B. \(b = R.\tan B.\) C. \(\sin C = \frac{{c\sin A}}{a}.\) D. \(a = 2R\sin A.\)
Câu 13: Cho đồ thị hàm số \(y = f\left( x \right)\) như hình vẽ
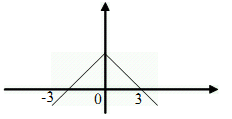
Kết luận nào trong các kết luận sau là đúng?
A. Hàm số đồng biến trên \(\mathbb{R}\). B. Tập xác định \(D = [ - 3;3]\).
C. Hàm số nghịch biến trên \((1;2)\) D. Cả ba đáp án đều sai.
Câu 14: Bảng biến thiên của hàm số \(y = - {x^2} + 2x - 1\) là:
A.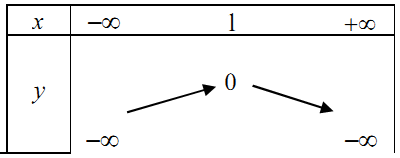 . B.
. B. 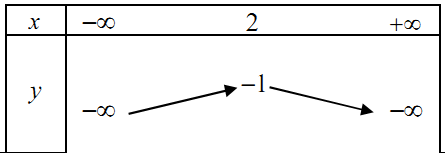 .
.
C. 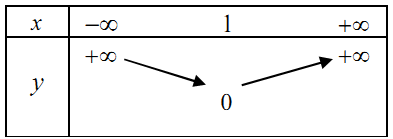 . D.
. D. 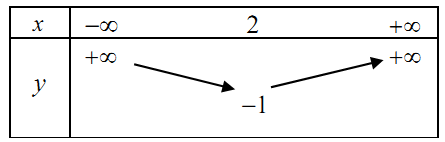 .
.
Câu 15: (ID: 591039) Cho hai tập hợp \(X = \left\{ {1;2;3;4} \right\}\), \(Y = \left\{ {1;2} \right\}\). Tập hợp \({C_X}Y\) là tập hợp nào sau đây?
A. \(\left\{ {3;4} \right\}.\) B. \(\left\{ {1;2;3;4} \right\}.\) C. \(\left\{ {1;2} \right\}.\) D. \(\emptyset .\)
Câu 16: Cho hàm số \(y = a{x^2} + bx + c\) có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?
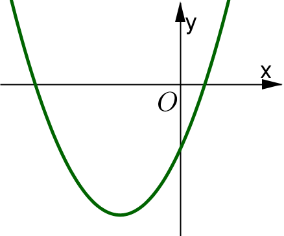
A. \(a > 0;{\rm{ }}b > 0;{\rm{ }}c > 0\). B. \(a > 0;{\rm{ }}b < 0;{\rm{ }}c > 0\). C. \(a > 0;{\rm{ }}b < 0;{\rm{ }}c < 0\). D. \(a > 0;{\rm{ }}b > 0;{\rm{ }}c < 0\).
Câu 17: (ID: 591062) Trong hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x + 3y - 2 \ge 0}\\{2x + y + 1 \le 0}\end{array}} \right.\). Trong các điểm sau, điểm nào thuộc miền nghiệm của hệ bất phương trình?
A. A(0;1). B. C(1;3). C. B(-1;1). D. D(-1;0).
Câu 18: Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số \(y = {x^2} - 4x + 3\) trên đoạn \(\left[ { - 1;4} \right]\) là
A. \( - 1\). B. \(2\). C. \(7\). D. \(8\).
Câu 19: (ID: 591058) Cho \(\tan \alpha {\rm{ \;}} = {\rm{ \;}} - 2\). Tính giá trị của biểu thức \(P = \frac{{2\sin \alpha {\rm{ \;}} + 3\cos \alpha }}{{3\sin \alpha {\rm{ \;}} - 2\cos \alpha }}\).
A. \(P = \frac{7}{4}.\) B. \(P = {\rm{ \;}} - \frac{1}{8}.\) C. \(P = {\rm{ \;}} - \frac{7}{4}.\) D. \(P = \frac{1}{8}.\)
Câu 20: (ID: 428923) Cho tam giác ABC có trung tuyến BM và trọng tâm \(G\). Đặt \(\overrightarrow {BC} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BA} {\rm{\;}} = b\). Hãy phân tích vectơ \(\overrightarrow {BG} \) theo \(\vec a\) và \(\vec b\).
A. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\) B. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{2}{3}\vec b\) C. \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{2}{3}\vec b\) D. \(\overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\vec a + \frac{1}{3}\vec b\)
Câu 21: (ID: 428861) Khẳng định nào sau đây là sai?
A. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {BC} ,k \ne 0\).
B. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AC} = k\overrightarrow {BC} ,k \ne 0\).
C. Ba điểm phân biệt \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} ,k \ne 0\).
D. Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\; = \;}}k\overrightarrow {AC} \).
Câu 22: (ID: 590921) Cho tam giác ABC biết AB = 5, AC = 7, BC = 6. Bán kính đường tròn nội tiếp tam giác xấp xỉ là:
A. 1,63 B. 1,71 C. 1,36 D. 1,06
Câu 23: Xác định parabol \(y = a{x^2} + bx + c\) biết (P) có đỉnh \(I(2;0)\) và \((P)\) cắt trục \(Oy\) tại điểm \(M(0; - 1)\).
A. \(\left( P \right):y = - \frac{1}{4}{x^2} - 3x - 1\) B. \(\left( P \right):y = - \frac{1}{4}{x^2} - x - 1\)
C. \(\left( P \right):y = - \frac{1}{4}{x^2} + x - 1\). D. \(\left( P \right):y = - \frac{1}{4}{x^2} + 2x - 1\)
Câu 24: (ID: 592001) Cho ba điểm không thẳng hàng A, B, C. Điều kiện cần và đủ để ba điểm A, B, C thỏa mãn điều kiện \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0\) là:
A. \(\Delta ABC\) đều. B. \(\Delta ABC\) cân tại C.
C. \(\Delta ABC\) vuông tại C. D. \(\Delta ABC\) vuông cân tại C.
Câu 25: (ID: 592017) Cho tam giác ABC vuông cân tại A, cạnh AC = a. Tính \(\overrightarrow {AB} .\overrightarrow {AC} \).
A. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = \vec 0.\) B. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = {a^2}.\) C. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = 0.\) D. \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = \sqrt 2 {a^2}.\)
Phần 2: Tự luận (5 điểm)
Câu 1: a) Xác định hàm số \(y = a{x^2} + bx + c\) biết đồ thị của nó có đỉnh \(I\left( {\frac{3}{2};\frac{1}{4}} \right)\) và cắt trục hoành tại điểm có hoành độ bằng \(2.\)
b) Xét sự biến thiên và vẽ đồ thị hàm số tìm được.
Câu 2: Cho tam giác ABC.
Tìm tập hợp các điểm M thỏa mãn điều kiện \(\left| {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} {\rm{ \;}} - 3\overrightarrow {MC} } \right|\).
Câu 3: Cho tam giác ABC có ba cạnh là a, b, c. Chứng minh rằng
\(\frac{{{a^2} + {b^2} + {c^2}}}{{2abc}} = \frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}\).
Câu 4: Tính chiều cao CD của cây trong hình vẽ dưới đây:
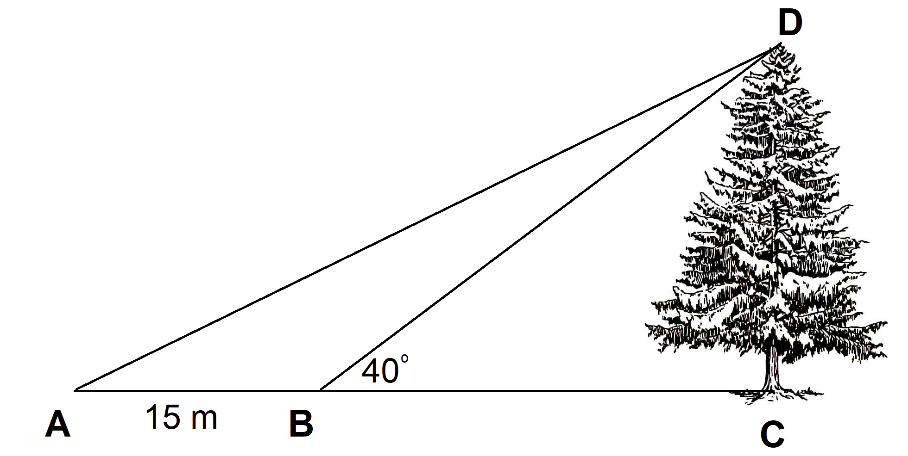
----- HẾT -----
Lời giải
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
|
1.B |
2.C |
3.B |
4.C |
5.C |
6.C |
7.B |
8.B |
9.D |
10.A |
|
11.C |
12.B |
13.C |
14.A |
15.A |
16.D |
17.C |
18.C |
19.D |
20.A |
|
21.D |
22.A |
23.C |
24.B |
25.C |
|
|
|
|
|
Câu 1 (NB):
Phương pháp:
Mệnh đề là câu khẳng định có tính đúng hoặc sai.
Cách giải:
Câu (3) không phải là mệnh đề.
Chọn B.
Câu 2 (TH):
Phương pháp:
Sử dụng công thức trung điểm: \(\overrightarrow {AM} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right)\).
Cách giải:
Vì M là trung điểm của BC nên
\(\begin{array}{*{20}{l}}{\overrightarrow {AM} {\rm{ \;}} = \frac{1}{2}\left( {\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} } \right)}\\{ \Leftrightarrow 2\overrightarrow {AM} {\rm{ \;}} = \overrightarrow {AB} {\rm{ \;}} + \overrightarrow {AC} }\\{ \Leftrightarrow \overrightarrow {AC} {\rm{ \;}} = {\rm{ \;}} - \overrightarrow {AB} {\rm{ \;}} + 2\overrightarrow {AM} }\\{ \Rightarrow x = {\rm{ \;}} - 1,{\mkern 1mu} {\mkern 1mu} y = 2.}\end{array}\)
Vậy cặp số (x;y) cần tìm là (-1;2).
Chọn C.
Câu 3 (TH):
Phương pháp:
Tính số HS thích học một trong hai môn.
Tính số HS thích học cả hai môn = Số HS thích môn Văn + số HS thích môn Toán – số HS thích một trong hai môn.
Cách giải:
Số học sinh thích môn Văn hoặc Toán là: 37 – 9 = 28 (bạn).
Số học sinh thích cả hai môn Văn và Toán là: (17 + 19) – 28 = 8 (bạn).
Chọn B.
Câu 4 (TH):
Phương pháp:
Giải từng bất phương trình.
Lấy giao hai tập hợp nghiệm của hai bất phương trình.
Cách giải:
Giải từng bất phương trình:
\(3x - 4 \ge 0 \Leftrightarrow x \ge \frac{4}{3} \Rightarrow {S_1} = \left[ {\frac{4}{3}; + \infty } \right)\).
\(\frac{{x - 1}}{2} - x \ge {\rm{ \;}} - 2 \Leftrightarrow x - 1 - 2x \ge {\rm{ \;}} - 2x \Leftrightarrow x \ge 1 \Rightarrow {S_2} = \left[ {1; + \infty } \right).\).
Vậy tập nghiệm của bất phương trình là \(S = {S_1} \cap {S_2} = \left[ {\frac{4}{3}; + \infty } \right).\)
Chọn C.
Câu 5 (TH):
Phương pháp:
Dựa vào các điểm thuộc miền nghiệm của bất phương trình.
Cách giải:
Thay tọa độ điểm (2;0) vào bất phương trình ta có: \(\left\{ {\begin{array}{*{20}{l}}{0 + 2 - 1 > 0}\\{2 \ge 2}\\{ - 0 + 2.2 > 3}\end{array}} \right.\) (đúng) nên điểm (0;2) thuộc miền nghiệm của hệ bất phương trình đã cho.
Dựa vào các đáp án ta thấy chỉ có đáp án C thỏa mãn.
Chọn C.
Câu 6 (VD):
Phương pháp:
Áp dụng định lí cosin trong tam giác ABC tính BC: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A\).
Sử dụng công thức tính diện tích tam giác: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A.\)
Sử dụng công thức \({S_{ABC}} = \frac{{AB.AC.BC}}{{4R}}\), từ đó suy ra R.
Cách giải:
Áp dụng định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{B{C^2} = A{B^2} + A{C^2} - 2AB.AC.\cos A}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {9^2} + {{18}^2} - 2.9.8.\cos {{60}^0} = 243}\\{ \Rightarrow BC = 9\sqrt 3 }\end{array}\)
Khi đó ta có: \({S_{ABC}} = \frac{1}{2}AB.AC.\sin A = \frac{1}{2}.9.18.\sin {60^0} = \frac{{81\sqrt 3 }}{2}\).
Mà \({S_{ABC}} = \frac{{AB.AC.BC}}{{4R}} \Rightarrow R = \frac{{AB.AC.BC}}{{4{S_{ABC}}}} = \frac{{9.18.9\sqrt 3 }}{{4.\frac{{81\sqrt 3 }}{2}}} = 9.\)
Chọn C.
Câu 7 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\).
Cách giải:
Xét tam giác ABC ta có: C = 1800 – (A + B) = 750.
Sử dụng định lí Sin trong tam giác ABC ta có: \(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}}\).
\( \Rightarrow AC = \frac{{AB}}{{\sin C}}.\sin B = \frac{8}{{\sin {{75}^0}}}.\sin {45^0} \approx 5,86.\)
Chọn B.
Câu 8 (TH):
Phương pháp:
Sử dụng \({\sin ^2}x + {\cos ^2}x = 1,{\mkern 1mu} {\mkern 1mu} \tan x = \frac{{\sin x}}{{\cos x}}\).
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{{{\tan }^2}x{{\sin }^2}x - {{\tan }^2}x + {{\sin }^2}x}\\{ = {{\tan }^2}x\left( {{{\sin }^2}x - 1} \right) + {{\sin }^2}x}\\{ = \frac{{{{\sin }^2}x}}{{{{\cos }^2}x}}.\left( { - {{\cos }^2}x} \right) + {{\sin }^2}x}\\{ = {\rm{ \;}} - {{\sin }^2}x + {{\sin }^2}x = 0.}\end{array}\)
Chọn B.
Câu 9 (VD):
Phương pháp:
Sử dụng quy tắc ba điểm, phép nhân vectơ với một số.
Cách giải:
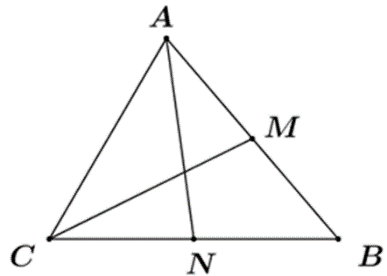
\(\begin{array}{*{20}{l}}{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} \overrightarrow {AB} = 2\overrightarrow {AM} = 2\left( {\overrightarrow {AN} + \overrightarrow {NC} + \overrightarrow {CM} } \right)}\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + \overrightarrow {BC} + 2\overrightarrow {CM} }\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + 2\overrightarrow {CM} + \left( {\overrightarrow {BM} - \overrightarrow {CM} } \right)}\\{ \Leftrightarrow \overrightarrow {AB} = 2\overrightarrow {AN} + 2\overrightarrow {CM} - \frac{1}{2}\overrightarrow {AB} - \overrightarrow {CM} }\\{ \Leftrightarrow \frac{3}{2}\overrightarrow {AB} = 2\overrightarrow {AN} + \overrightarrow {CM} }\\{ \Leftrightarrow \overrightarrow {AB} = \frac{4}{3}\overrightarrow {AN} + \frac{2}{3}\overrightarrow {CM} }\end{array}\)
Chọn D.
Câu 10 (TH):
Phương pháp:
Cho tam giác ABC trọng tâm G và điểm M bất kì, ta có \(\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = 3\overrightarrow {MG} .\)
Cách giải:
Theo bài ra ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + 4\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow \left( {\overrightarrow {MA} {\rm{ \;}} + \overrightarrow {MB} {\rm{ \;}} + \overrightarrow {MC} } \right) + 3\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow 3\overrightarrow {MG} {\rm{ \;}} + 3\overrightarrow {MC} {\rm{ \;}} = \vec 0}\\{ \Leftrightarrow \overrightarrow {MG} {\rm{ \;}} + \overrightarrow {MC} {\rm{ \;}} = \vec 0}\end{array}\)
=> M là trung điểm của GC.
Vậy M thuộc miền 1.
Chọn A.
Câu 11 (TH):
Phương pháp:
\(\sqrt {f(x)} \) xác định khi \(f(x) \ge 0\)
\(\frac{1}{{g(x)}}\) xác định khi \(g(x) \ne 0\)
Cách giải:
Hàm số \(y = \frac{{\sqrt {2x + 1} }}{{3 - x}}\) xác định khi \(\left\{ \begin{array}{l}2x + 1 \ge 0\\3 - x \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - \frac{1}{2}\\x \ne 3\end{array} \right.\)
Vậy tập xác định \(D = \left[ { - \frac{1}{2}; + \infty } \right)\backslash \left\{ 3 \right\}\)
Chọn C.
Câu 12 (TH):
Phương pháp:
Sử dụng định lí Sin trong tam giác: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R\).
Cách giải:
Sử dụng định lí Sin trong tam giác ta có:
\(\begin{array}{*{20}{l}}{\frac{a}{{\sin A}} = \frac{b}{{\sin B}} = \frac{c}{{\sin C}} = 2R}\\{ \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a = \frac{{b\sin A}}{{\sin B}}}\\{\sin c = \frac{{c\sin A}}{a}}\\{a = 2R\sin A}\end{array}} \right.}\end{array}\)
Suy ra A, C, D đúng.
Chọn B.
Câu 13 (NB):
Phương pháp:
Quan sát đồ thị và kết luận
Cách giải:
Quan sát đồ thị hàm số \(y = f\left( x \right)\) ta thấy

Đồ thị kéo dài qua điểm (-3;0) và (3;0) nên tập xác định \(D \ne [ - 3;3]\) (loại B).
Trên (0;3): Đồ thị đi xuống từ trái qua phải => Hàm số nghịch biến trên (0;3) (loại A)
=> Hàm số nghịch biến trên (1;2) vì \((1;2) \subset (0;3).\)
Chọn C.
Câu 14 (TH):
Cách giải:
Hàm số\(y = - {x^2} + 2x - 1\) có \(a = - 1,b = 2\)
Vì \(a = - 1 < 0\), nên loại C và D.
Hoành độ đỉnh \( - \frac{b}{{2a}} = - \frac{2}{{2.( - 1)}} = 1\), tung độ đỉnh \(y(1) = - {1^2} + 2.1 - 1 = 0\)
Chọn A.
Câu 15 (NB):
Phương pháp:
\({C_X}Y = X\backslash Y = \{ x \in X\) và \(x \notin Y\} .\)
Cách giải:
Ta có: \({C_X}Y = X\backslash Y = \left\{ {3;4} \right\}.\)
Chọn A.
Câu 16 (NB):
Phương pháp:
Quan sát đồ thị
Cách giải:
Vì Parabol hướng bề lõm lên trên nên \(a > 0\).
Đồ thị hàm số cắt \(Oy\) tại điểm \(\left( {0;c} \right)\) ở dưới \(Ox \Rightarrow c < 0\)(Loại A, B).
Hoành độ đỉnh Parabol là \( - \frac{b}{{2a}} < 0\), mà \(a > 0 \Rightarrow b > 0\)(Loại C)
Chọn D.
Câu 17 (TH):
Phương pháp:
Thay trực tiếp tọa độ các điểm ở các đáp án vào hệ bất phương trình.
Cách giải:
Thay tọa độ điểm A(0;1) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{0 + 3.1 - 2 \ge 0}\\{2.0 + 1 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{1 \ge 0}\\{2 \le 0}\end{array}} \right.\) (sai)
Thay tọa độ điểm C(1;3) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{1 + 3.3 - 2 \ge 0}\\{2.1 + 3 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{8 \ge 0}\\{6 \le 0}\end{array}} \right.\) (sai)
Thay tọa độ điểm B(-1;1) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ - 1 + 3.1 - 2 \ge 0}\\{2\left( { - 1} \right) + 1 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{0 \ge 0}\\{0 \le 0}\end{array}} \right.\) (đúng)
Thay tọa độ điểm D(-1;0) vào bất phương trình: \(\left\{ {\begin{array}{*{20}{l}}{ - 1 + 3.0 - 2 \ge 0}\\{2\left( { - 1} \right) + 0 + 1 \le 0}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{ - 3 \ge 0}\\{ - 1 \le 0}\end{array}} \right.\) (sai)
Vậy điểm B(-1;1) thuộc miền nghiệm của hệ bất phương trình.
Chọn C.
Câu 18 (VD):
Cách giải:
Hàm số \(y = {x^2} - 4x + 3\) có \(a = 1 > 0,b = - 4 \Rightarrow - \frac{b}{{2a}} = - \frac{{ - 4}}{{2.1}} = 2;y(2) = - 1.\)
\(y( - 1) = 8;y(4) = 3\)
Ta có bảng biến thiên trên \(\left[ { - 1;4} \right]\) là:
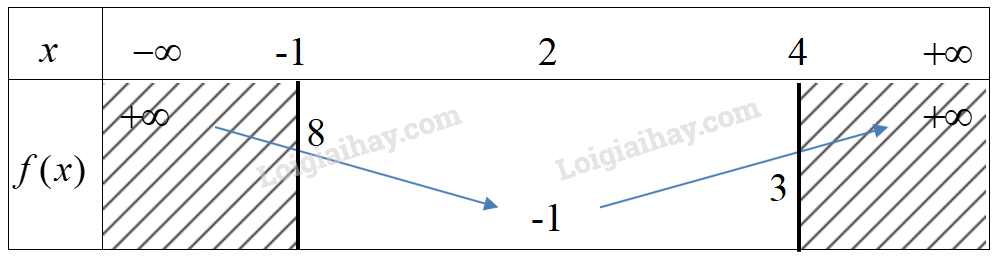
Từ bảng biến thiên suy ra:
Trên \(\left[ { - 1;4} \right]\): Giá trị lớn nhất của hàm số bằng \(8\) và giá trị nhỏ nhất của hàm số bằng \( - 1\)
Tổng giá trị lớn nhất và giá trị nhỏ nhất là \(8 + \left( { - 1} \right) = 7\).
Chọn C.
Câu 19 (VD):
Phương pháp:
Chia cả tử và mẫu biểu thức P cho \cos \alpha và biểu diễn biểu thức P theo \tan \alpha .
Cách giải:
Vì \(\tan \alpha {\rm{ \;}} = {\rm{ \;}} - 2\) xác định nên \(\cos \alpha {\rm{ \;}} \ne 0.\)
Chia cả tử và mẫu của biểu thức P cho \(\cos \alpha \) ta được:
\(\begin{array}{*{20}{l}}{P = \frac{{2\sin \alpha {\rm{ \;}} + 3\cos \alpha }}{{3\sin \alpha {\rm{ \;}} - 2\cos \alpha }} = \frac{{2\frac{{\sin \alpha }}{{\cos \alpha }} + 3}}{{3\frac{{\sin \alpha }}{{\cos \alpha }} - 2}}}\\{{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = \frac{{2\tan \alpha {\rm{ \;}} + 3}}{{3\tan \alpha {\rm{ \;}} - 2}} = \frac{{2.\left( { - 2} \right) + 3}}{{3.\left( { - 2} \right) - 2}} = \frac{{ - 1}}{{ - 8}} = \frac{1}{8}.}\end{array}\)
Chọn D.
Câu 20 (TH):
Phương pháp:
Áp dụng quy tắc cộng vecto, quy tắc hình bình hành để biểu diễn véctơ.
Cách giải:
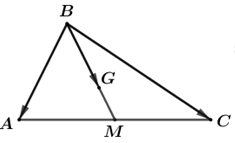
\(\overrightarrow {BM} {\rm{\;}} = \frac{1}{2}\left( {\overrightarrow {BA} {\rm{\;}} + \overrightarrow {BC} } \right) = \frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {BG} {\rm{\;}} = \frac{2}{3}\overrightarrow {BM} {\rm{\;}} = \frac{2}{3} \cdot \left( {\frac{1}{2}\overrightarrow {BA} {\rm{\;}} + \frac{1}{2}\overrightarrow {BC} } \right) = \frac{1}{3}\overrightarrow {BA} {\rm{\;}} + \frac{1}{3}\overrightarrow {BC} \)
Mặt khác, \(\overrightarrow {BA} {\rm{\;}} = \vec a,{\mkern 1mu} {\mkern 1mu} \overrightarrow {BC} {\rm{\;}} = \vec b\) nên ta có: \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\)
Vậy \(\overrightarrow {BG} {\rm{\;}} = \frac{1}{3}\vec a + \frac{1}{3}\vec b\).
Chọn A.
Câu 21 (NB):
Phương pháp:
Áp dụng điều kiện để hai vecto cùng phương. Điều kiện cần và đủ để ba điểm thẳng hàng.
Cách giải:
Theo lý thuyết, ba điểm \(A,{\mkern 1mu} {\mkern 1mu} B,{\mkern 1mu} {\mkern 1mu} C\) phân biệt thẳng hàng khi và chỉ khi tồn tại \(k\) khác \(0\) sao cho \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} \).
Do vậy, khẳng định sai là: Ba điểm phân biệt \(A,B,C\) thẳng hàng khi và chỉ khi \(\overrightarrow {AB} {\rm{\; = \;}}k\overrightarrow {AC} \).
Vì xảy ra trường hợp \(k = 0\), khi đó \(\overrightarrow {AB} {\rm{\;}} = k\overrightarrow {AC} {\rm{\;}} = 0.\overrightarrow {AC} {\rm{\;}} = 0\) (vô lý)
Chọn D.
Câu 22 (NB):
Phương pháp:
Dùng công thức diện tích \(S = pr = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} \)
Cách giải:
\(\begin{array}{*{20}{l}}{S = pr = \sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }\\{ \Rightarrow r = \frac{{\sqrt {p\left( {p - a} \right)\left( {p - b} \right)\left( {p - c} \right)} }}{p} = 1,63}\end{array}\)
với \(p = \frac{{a + b + c}}{2} = 9\)
Chọn A.
Câu 23 (VD):
Phương pháp:
Parabol \(\left( P \right):y = a{x^2} + bx + c\) có đỉnh \(I\left( { - \frac{b}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) và cắt Oy tại (0;c).
Cách giải:
Ta có (P) cắt Oy tại điểm \(M\left( {0; - 1} \right)\) suy ra \(y\left( 0 \right) = - 1 \Leftrightarrow c = - 1\)
Lại có: đỉnh \(I\left( {2;0} \right) \Rightarrow \left\{ \begin{array}{l} - \frac{b}{{2a}} = 2\\a{.2^2} + b.2 + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = - 4a\\4a + 2b - 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - \frac{1}{4}\\b = 1\end{array} \right.\)
Vậy parabol đó là \(\left( P \right):y = - \frac{1}{4}{x^2} + x - 1\)
Chọn C.
Câu 24 (TH):
Phương pháp:
Sử dụng quy tắc hình bình hành.
Sử dụng: hai vectơ vuông góc với nhau thì tích vô hướng bằng 0.
Cách giải:
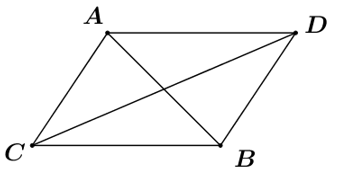
Lấy D sao cho ACBD là hình bình hành, khi đó ta có: \(\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} {\rm{ \;}} = \overrightarrow {CD} \).
Theo bài ra ta có: \(\left( {\overrightarrow {CA} {\rm{ \;}} + \overrightarrow {CB} } \right).\overrightarrow {AB} {\rm{ \;}} = 0 \Leftrightarrow \overrightarrow {CD} .\overrightarrow {AB} {\rm{ \;}} = 0\) \( \Rightarrow CD \bot AB\).
Hình bình hành ACBD có hai đường chéo vuông góc nên là hình thoi, do đó CA = CB.
Vậy tam giác ABC cân tại C.
Chọn B.
Câu 25 (NB):
Phương pháp:
Sử dụng định nghĩa tích vô hướng của hai vectơ: \(\vec a.\vec b{\rm{ \;}} = \left| {\vec a} \right|.\left| {\vec b} \right|.\cos \left( {\vec a,\vec b} \right)\).
Cách giải:
Vì tam giác ABC vuông cân tại A nên \(AB \bot AC\).
Vậy \(\overrightarrow {AB} .\overrightarrow {AC} {\rm{ \;}} = 0.\)
Chọn C.
Phần 2: Tự luận (4 điểm)
Câu 1 (VD):
Phương pháp:
Phương pháp:
a) Hàm số \(y = a{x^2} + bx + c(a \ne 0)\) có đỉnh \(I\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
b) Sự biến thiên 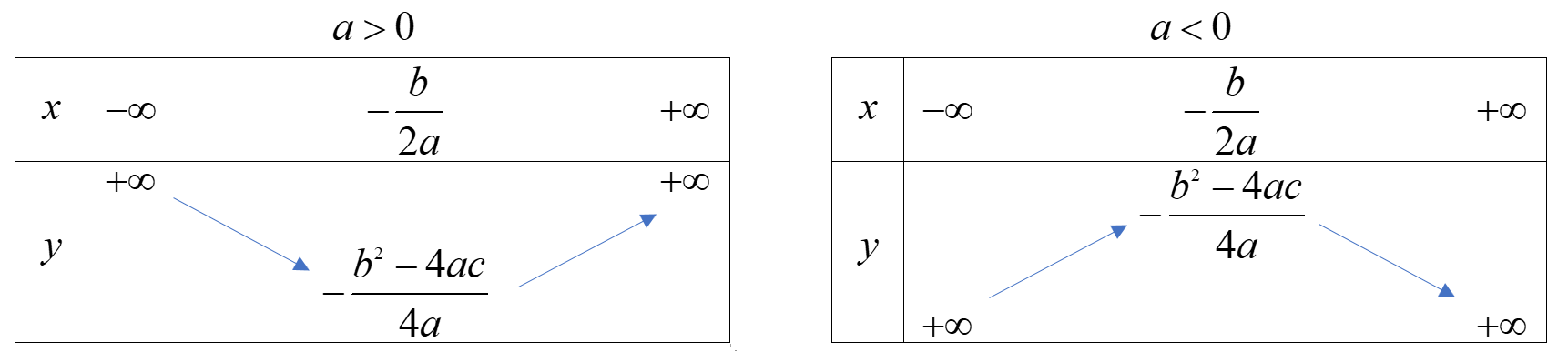
* Vẽ đồ thị
+ Đỉnh I\(\left( { - \frac{b}{{2a}};\frac{{ - \Delta }}{{4a}}} \right)\)
+ Trục đối xứng \(x = - \frac{b}{{2a}}\)
+ Giao với các trục (nếu có)
+ Lấy các điểm thuộc đồ thị (đối xứng nhau qua trục đối xứng).
Cách giải:
a) Ta có: Parabol cắt trục hoành tại điểm có hoành độ bằng \(2\) nên \(y(2) = 0 \Leftrightarrow 4a + 2b + c = 0\)
Đồ thị của nó có đỉnh \(I\left( {\frac{3}{2};\frac{1}{4}} \right)\) nên \(\left\{ \begin{array}{l}\frac{{ - b}}{{2a}} = \frac{3}{2}\\{\left( {\frac{3}{2}} \right)^2}a + \frac{3}{2}b + c = \frac{1}{4}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3a + b = 0\\9a + 6b + 4c = 1\end{array} \right.\)
Kết hợp, ta được hệ \(\left\{ \begin{array}{l}3a + b = 0\\9a + 6b + 4c = 1\\4a + 2b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 3\\c = - 2\end{array} \right.\)
Vậy parabol đó là \(y = - {x^2} + 3x - 2\)
b) Hàm số \(y = - {x^2} + 3x - 2\) có \(a = - 1 < 0\) và đỉnh là \(I\left( {\frac{3}{2};\frac{1}{4}} \right)\)
Ta có bảng biến thiên:
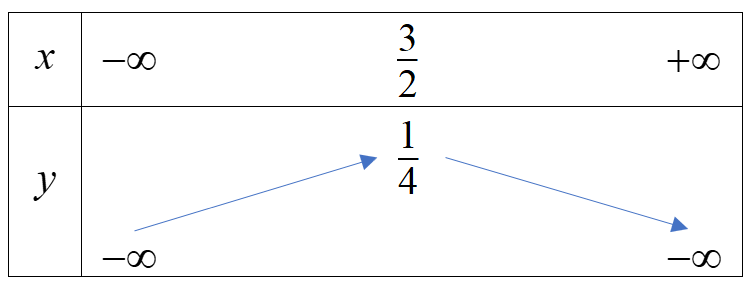
Hàm số đồng biến trên \(( - \infty ;\frac{3}{2})\) và nghịch biến trên \((\frac{3}{2}; + \infty )\)
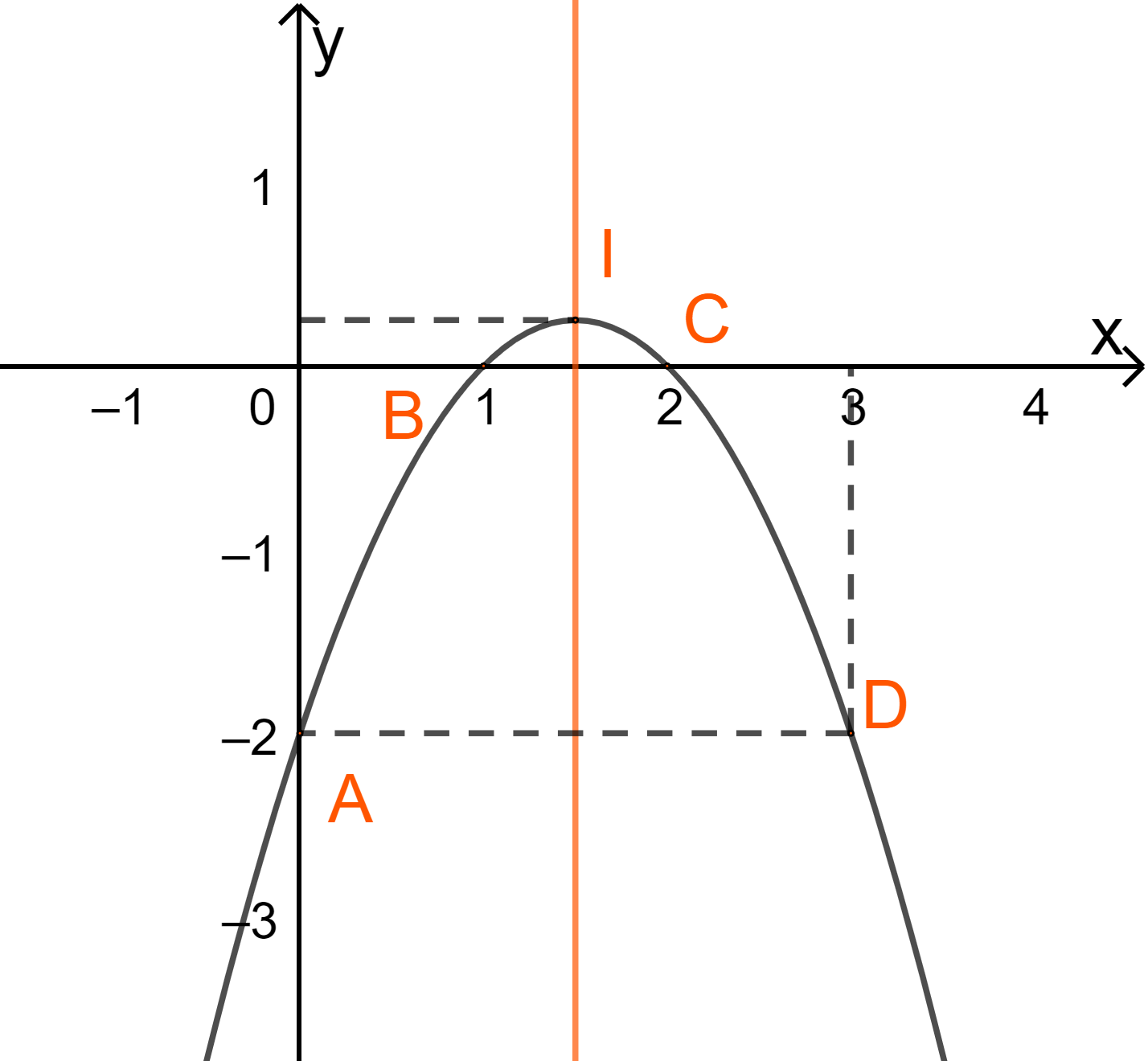
* Vẽ đồ thị hàm số
Đỉnh \(I\left( {\frac{3}{2};\frac{1}{4}} \right)\)
Trục đối xứng \(x = \frac{3}{2}\)
Cắt trục tung tại A(0;-2) và cắt Ox tại B(1;0) và C(2;0)
Lấy D(3;-2) thuộc (P), đối xứng với A(0;-2) qua trục đối xứng
Câu 2 (VD):
Phương pháp:
Gọi I là trung điểm của AB, J là điểm nằm trên đường thẳng AC thỏa mãn điều kiện \(\overrightarrow {JA} = 3\overrightarrow {JC} \)\( \Leftrightarrow \overrightarrow {JA} - 3\overrightarrow {JC} = \vec 0\)
Đưa đẳng thức đã cho về dạng MI = MJ, sử dụng công thức trung điểm, quy tắc ba điểm. Từ đó suy ra tập hợp điểm M.
Cách giải:
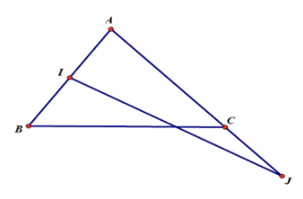
Gọi I là trung điểm của AB, J là điểm nằm trên đường thẳng AC thỏa mãn điều kiện \(\overrightarrow {JA} = 3\overrightarrow {JC} \)\( \Leftrightarrow \overrightarrow {JA} - 3\overrightarrow {JC} = \vec 0\)
Khi đó ta có:
\(\begin{array}{*{20}{l}}{\left| {\overrightarrow {MA} + \overrightarrow {MB} } \right| = \left| {\overrightarrow {MA} - 3\overrightarrow {MC} } \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| {\overrightarrow {MJ} + \overrightarrow {JA} - 3\left( {\overrightarrow {MJ} + \overrightarrow {JC} } \right)} \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| { - 2\overrightarrow {MJ} + \left( {\overrightarrow {JA} - 3\overrightarrow {JC} } \right)} \right|}\\{ \Leftrightarrow \left| {2\overrightarrow {MI} } \right| = \left| { - 2\overrightarrow {MJ} } \right|}\\{ \Leftrightarrow MI = MJ}\end{array}\)
Vậy tập hợp các điểm M là đường trung trực của IJ.
Câu 3 (VDC):
Phương pháp:
Sử dụng \(\overrightarrow {AB} {\rm{ \;}} + \overrightarrow {BC} {\rm{ \;}} + \overrightarrow {CA} {\rm{ \;}} = \vec 0\), bình phương hai vế, sử dụng khái niệm tích vô hướng của 2 vectơ.
Cách giải:
Ta có:
\(\begin{array}{*{20}{l}}{\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} = \vec 0}\\{ \Rightarrow {{\left( {\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CA} } \right)}^2} = 0}\\{ \Leftrightarrow {{\overrightarrow {AB} }^2} + {{\overrightarrow {BC} }^2} + {{\overrightarrow {CA} }^2} + 2\overrightarrow {AB} .\overrightarrow {BC} + 2\overrightarrow {BC} .\overrightarrow {CA} + 2\overrightarrow {CA} .\overrightarrow {AB} = 0}\\{ \Leftrightarrow {a^2} + {b^2} + {c^2} = 2\overrightarrow {BA} .\overrightarrow {BC} + 2\overrightarrow {CB} .\overrightarrow {CA} + 2\overrightarrow {AC} .\overrightarrow {AC} }\\{ \Leftrightarrow {a^2} + {b^2} + {c^2} = 2ac\cos B + 2bc\cos A + 2ab\cos C}\\{ \Leftrightarrow \frac{{{a^2} + {b^2} + {c^2}}}{{2abc}} = \frac{{\cos A}}{a} + \frac{{\cos B}}{b} + \frac{{\cos C}}{c}{\mkern 1mu} \left( {dpcm} \right).}\end{array}\)
Mặt khác, theo định lí cosin trong tam giác ABC ta có:
\(\begin{array}{*{20}{l}}{{a^2} = {b^2} + {c^2} - 2bc\cos A}\\{ \Leftrightarrow {a^2} = 5{a^2} - 2bc\cos A}\\{ \Leftrightarrow 2bc\cos A = 4{a^2}}\\{ \Leftrightarrow bc = \frac{{2{a^2}}}{{\cos A}} = \frac{{2{a^2}}}{{\cos \alpha }}}\end{array}\)
Vậy \({S_{\Delta ABC}} = \frac{1}{2}bc\sin A = \frac{1}{2}\frac{{2{a^2}}}{{2\cos \alpha }}\sin \alpha {\rm{ \;}} = {a^2}\tan \alpha .\)
Câu 4 (VD):
Cách giải:
Ta có: \(\widehat {DBA} = {180^ \circ } - \widehat {DBC} = {180^ \circ } - {40^ \circ } = {140^ \circ } \Rightarrow \widehat {ADB} = {180^ \circ } - {30^ \circ } - {140^ \circ } = {10^ \circ }\)
Áp dụng định lí sin trong \(\Delta ADB\) ta có:
\(\begin{array}{l}\frac{{AB}}{{\sin D}} = \frac{{AD}}{{\sin B}} \Leftrightarrow \frac{{15}}{{\sin {{10}^ \circ }}} = \frac{{AD}}{{\sin {{140}^ \circ }}}\\ \Rightarrow AD = \sin {140^ \circ }.\frac{{15}}{{\sin {{10}^ \circ }}}\end{array}\)
Lại có: \(CD = AD.\sin A = AD.\sin {30^ \circ }\)
\( \Rightarrow CD = \sin {140^ \circ }.\frac{{15}}{{\sin {{10}^ \circ }}}.\sin {30^ \circ } \approx 27,76\;(m)\)
Vậy cây đó cao khoảng 27,76m.












Danh sách bình luận