-
Đề khảo sát chất lượng đầu năm
-
Đề thi giữa kì 1 Toán 10
- Đề thi giữa kì 1 - Đề số 1
- Đề thi giữa kì 1 - Đề số 2
- Đề thi giữa kì 1 - Đề số 3
- Đề thi giữa kì 1 - Đề số 4
- Đề thi giữa kì 1 - Đề số 5
- Đề thi giữa kì 1 - Đề số 6
- Đề thi giữa kì 1 - Đề số 7
- Đề thi giữa kì 1 - Đề số 8
- Đề thi giữa kì 1 - Đề số 9
- Đề thi giữa kì 1 - Đề số 10
- Đề thi giữa kì 1 - Đề số 11
- Đề thi giữa kì 1 - Đề số 12
- Đề thi giữa kì 1 - Đề số 13
-
Đề thi học kì 1
- Đề cương ôn tập học kì 1
- Đề thi học kì 1 Toán 10 - Đề số 1
- Đề thi học kì 1 Toán 10 - Đề số 2
- Đề thi học kì 1 Toán 10 - Đề số 3
- Đề thi học kì 1 Toán 10 - Đề số 4
- Đề thi học kì 1 Toán 10 - Đề số 5
- Đề thi học kì 1 Toán 10 - Đề số 6
- Đề thi học kì 1 Toán 10 - Đề số 7
- Đề thi học kì 1 Toán 10 - Đề số 8
- Đề thi học kì 1 Toán 10 - Đề số 9
- Đề thi học kì 1 Toán 10 - Đề số 10
- Đề thi học kì 1 Toán 10 - Đề số 11
- Đề thi học kì 1 Toán 10 - Đề số 12
- Đề thi học kì 1 Toán 10 - Đề số 13
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề khảo sát chất lượng đầu năm Toán 10 Cánh diều - Đề số 3
Tổng hợp đề thi học kì 1 lớp 10 tất cả các môn - Cánh diều
Toán - Văn - Anh - Lí - Hóa - Sinh - Sử - Địa...
Đề bài
Số đường tròn nội tiếp của một đa giác đều là
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình \( - 3{x^2} + 5x + 1 = 0\).
-
A.
\( - \dfrac{5}{6}\)
-
B.
\(\dfrac{5}{6}\)
-
C.
\( - \dfrac{5}{3}\)
-
D.
\(\dfrac{5}{3}\)
Rút gọn biểu thức \(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) với \(a > 0\) ta được:
-
A.
\(\dfrac{{47}}{{10}}\sqrt a \)
-
B.
\(\dfrac{{21}}{5}\sqrt a \)
-
C.
\(\dfrac{{47}}{{10}}\sqrt {2a} \)
-
D.
\(\dfrac{{47}}{5}\sqrt {2a} \)
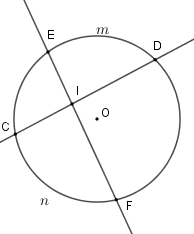
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Hàm số nào sau đây là hàm số đồng biến?
-
A.
\(y = - \left( {\dfrac{x}{2} - 3} \right)\)
-
B.
\(y = \dfrac{{\sqrt 3 }}{2}\left( {x + 1} \right)\)
-
C.
\(y = - 5 - 3x\)
-
D.
\(y = - \left( {9 + 3x} \right)\)
Hệ phương trình \(\left\{ \begin{array}{l}{x^2} = 3x - y\\{y^2} = 3y - x\end{array} \right.\) có bao nhiêu cặp nghiệm \(\left( {x;y} \right)\) ?
-
A.
\(1.\)
-
B.
\(2.\)
-
C.
\(3.\)
-
D.
\(4.\)
Tập nghiệm của phương trình \(\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}} = 2\) là:
-
A.
\(S = \left\{ {1; - 7} \right\}\)
-
B.
\(S = \left\{ { - 1;7} \right\}\)
-
C.
\(S = \left\{ 7 \right\}\)
-
D.
\(S = \left\{ { - 1} \right\}\)
Chọn khẳng định đúng. Góc ở tâm là góc
-
A.
Có đỉnh nằm trên đường tròn
-
B.
Có đỉnh trùng với tâm đường tròn
-
C.
Có hai cạnh là hai đường kính của đường tròn
-
D.
Có đỉnh nằm trên bán kính của đường tròn
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi:
-
A.
\(m \notin \left\{ {0;\dfrac{1}{2}} \right\}\)
-
B.
\(m > 0\)
-
C.
\(m \ne 0\)
-
D.
\(m \ne \dfrac{1}{2}\)
Cho hàm số \(y = f\left( x \right) = \dfrac{1}{2}{x^2}\) . Tổng các giá trị của \(a\) thỏa mãn \(f\left( a \right) = 3 + \sqrt 5 \) là
-
A.
\(1\)
-
B.
\(2\sqrt 5 \)
-
C.
\(0\)
-
D.
\( - 2\)
Viết phương trình đường thẳng \(d\) biết \(d\) tạo với đường thẳng \(y = 2\) (theo chiều dương) một góc bằng \(135^\circ \) và cắt trục tung tại điểm có tung độ bằng \(4\).
-
A.
\(y = x - 4\)
-
B.
\(y = - x - 4\)
-
C.
\(y = x + 4\)
-
D.
\(y = - x + 4\)
Phép tính \(\sqrt {{{12}^2}.{{\left( { - 11} \right)}^2}} \) có kết quả là?
-
A.
\( - 33\)
-
B.
\( - 132\)
-
C.
\(132\)
-
D.
Không tồn tại.
Cho hai số tự nhiên biết rằng số thứ nhất lớn hơn hai lần số thứ hai là \(3\) và hiệu các bình phương của chúng bằng \(360\) . Tìm số bé hơn.
-
A.
\(12\)
-
B.
\(10\)
-
C.
\(21\)
-
D.
\(9\)
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
-
A.
$BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 32'$
-
B.
$BC = \sqrt {74} (cm);\widehat C \approx 36^\circ 32'$
-
C.
$BC = \sqrt {74} (cm) ;\widehat C \approx 35^\circ 33'$
-
D.
$BC = \sqrt {75} (cm) ;\widehat C \approx 35^\circ 32'$
Cho tam giác \(ABC\) có các đường cao \(BD,CE\) . Chọn khẳng định đúng.
-
A.
Bốn điểm \(B,E,D,C\) cùng nằm trên một đường tròn
-
B.
Năm điểm \(A,B,E,D,C\) cùng nằm trên một đường tròn
-
C.
Cả A, B đều sai
-
D.
Cả A, B đều đúng
Phương trình \({(2x + 1)^4}-8{(2x + 1)^2}-9 = 0\) có tổng các nghiệm là
-
A.
\(1\)
-
B.
\( - 2\)
-
C.
\( - 1\)
-
D.
\(2\sqrt 2 \)
Cho parabol\((P):y = 5{x^2}\) và đường thẳng \((d):y = - 4x - 4\). Số giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là:
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(3\)
-
D.
\(2\)
Đồ thị hàm số \(y = 5x - \dfrac{2}{5}\) đi qua điểm nào dưới đây?
-
A.
\(A\left( {1;\dfrac{{22}}{5}} \right)\)
-
B.
\(B\left( {\dfrac{1}{5};\dfrac{3}{5}} \right)\)
-
C.
\(C\left( { - \dfrac{2}{{25}}; - \dfrac{3}{5}} \right)\)
-
D.
\(D\left( {2;10} \right)\)
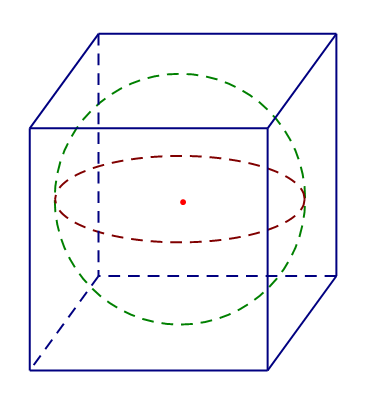
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Nếu diện tích diện tích toàn phần của hình lập phương là \(24c{m^2}\) thì diện tích mặt cầu là:
-
A.
\(4\pi \)
-
B.
\(4\)
-
C.
\(2\pi \)
-
D.
\(2\)
Phương trình \(\sqrt {{x^2} - 2x + 10} + \sqrt {6{x^2} - 12x + 31} = 8\) có nghiệm là
-
A.
Số lẻ dương
-
B.
Số chẵn dương
-
C.
Số lẻ âm
-
D.
Số vô tỉ
Một cột đèn điện \(AB\) cao \(7m\) có bóng in trên mặt đất là \(AC\) dài \(4m.\) Hãy tính góc \(\widehat {BCA}\) (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
-
A.
\(59^\circ 45'\)
-
B.
\(62^\circ \)
-
C.
\(61^\circ 15'\)
-
D.
\(60^\circ 15'\)
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 10cm\) và đường kính đáy là \(d= 6cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(129\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(69\pi \,\left( {c{m^2}} \right)\)
Một phòng họp có 360 ghế ngồi được xếp thành từng dãy và số ghế của từng dãy đều như nhau. Nếu số dãy tăng thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400 ghế. Hỏi trong phòng họp có bao nhiêu dãy ghế (biết số dãy ghế ít hơn 20).
-
A.
14 dãy
-
B.
15 dãy
-
C.
16 dãy
-
D.
17 dãy
Thu gọn $\sqrt[3]{{125{a^3}}}$ ta được
-
A.
$25a$
-
B.
$5a$
-
C.
$ - 25{a^3}$
-
D.
$ - 5a$
Không dùng bảng số và máy tính, hãy so sánh \(\cot 50^\circ \) và \(\cot 46^\circ \)
-
A.
\(\cot 46^\circ = \cot 50^\circ \)
-
B.
\(\cot 46^\circ > \cot 50^\circ \)
-
C.
\(\cot 46^\circ < \cot 50^\circ \)
-
D.
\(\cot 46^\circ \ge \cot 50^\circ \)
Cho đường thẳng \(d\):\(y = \dfrac{1}{3}x - 10\). Hệ số góc của đường thẳng \(d\) là
-
A.
\(3\)
-
B.
\(\dfrac{1}{3}\)
-
C.
\( - \dfrac{1}{3}\)
-
D.
\( - 3\)
Cho hai vòi nước cùng lúc chảy vào một bể cạn. Nếu chảy riêng từng vòi thì vòi thứ nhất chảy đầy bể chậm hơn vòi thứ hai \(2\) giờ. Khi nước đầy bể, người ta khóa vòi thứ nhất và vòi thứ hai lại, đồng thời mở vòi thứ ba cho nước chảy ra thì sau \(7,5\) giờ bể cạn nước. Khi nước trong bể đã cạn mở cả ba vòi thì sau \(20\) giờ bể lại đầy nước. Hỏi nếu chỉ dùng vòi thứ nhất thì sau bao lâu bể đầy nước?
-
A.
\(9\) giờ
-
B.
\(12\) giờ
-
C.
\(10\) giờ
-
D.
\(8\) giờ
Phát biểu nào sau đây đúng nhất
-
A.
Mỗi tam giác luôn có một đường tròn ngoại tiếp
-
B.
Mỗi tứ giác luôn có một đường tròn nội tiếp
-
C.
Cả A và B đều đúng
-
D.
Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó
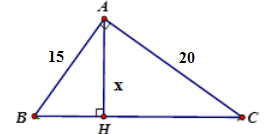
Tính \(x\) trong hình vẽ sau:
-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Cho hai hàm số \(f\left( x \right) = 6{x^4}\) và \(h\left( x \right) = 7 - \dfrac{{3.x}}{2}\). So sánh \(f\left( { - 1} \right)\) và \(h\left( {\dfrac{2}{3}} \right)\)
-
A.
\(f\left( { - 1} \right) = h\left( {\dfrac{2}{3}} \right)\)
-
B.
\(f\left( { - 1} \right) > h\left( {\dfrac{2}{3}} \right)\)
-
C.
\(f\left( { - 1} \right) < h\left( {\dfrac{2}{3}} \right)\)
-
D.
Không đủ điều kiện so sánh
Tìm \(m\) để hai phương trình \({x^2} + mx + 2 = 0\) và \({x^2} + 2x + m = 0\) có ít nhất một nghiệm chung.
-
A.
\(1\)
-
B.
\( - 3\)
-
C.
\( - 1\)
-
D.
\(3\)
Tìm cặp giá trị \((m;n)\) để hai hệ phương trình sau tương đương \(\left\{ \begin{array}{l}3x + 3y = 3\\x + \dfrac{1}{3}y = \dfrac{1}{3}\end{array} \right.(I)\) và
$\left\{ \begin{array}{l}{\rm{x}} - ny = 1\\3mx + my = 1\end{array} \right.(II)$
-
A.
\(\left( {1;\dfrac{1}{2}} \right)\)
-
B.
\(\left( 1;-1 \right)\)
-
C.
\(( - 1;1)\)
-
D.
\(\left( {\dfrac{1}{2}; - 1} \right)\)
Rút gọn biểu thức sau \(\sqrt {{{\left( {5 - \sqrt {11} } \right)}^2}} + \sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} \).
-
A.
\(2 + 2\sqrt {11} \)
-
B.
\(8\)
-
C.
\(2\)
-
D.
\(2\sqrt {11} \)
Đưa thừa số \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \) (\(x < 0\)) vào trong dấu căn ta được:
-
A.
\(\sqrt {\dfrac{{300}}{x}} \)
-
B.
\(\sqrt {\dfrac{{ - 300}}{x}} \)
-
C.
\( - \sqrt {\dfrac{{ - 300}}{x}} \)
-
D.
\( - \sqrt {\dfrac{{ - 60}}{x}} \)
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt các đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt các đường thẳng AB tại I. Chọn đáp án đúng.
-
A.
Các tam giác $FNI,{\rm{ }}INE$ cân
-
B.
$\widehat {IEN} = 2\widehat {NDC}$
-
C.
$\widehat {DNI} = 3\widehat {DCN}$
-
D.
Tất cả các câu đều sai
Lời giải và đáp án
Số đường tròn nội tiếp của một đa giác đều là
-
A.
\(1\)
-
B.
\(2\)
-
C.
\(3\)
-
D.
\(0\)
Đáp án : A
Bất kì đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
So sánh hai số \(5\) và \(\sqrt {50} - 2\).
-
A.
\(5 > \sqrt {50} - 2\)
-
B.
\(5 = \sqrt {50} - 2\)
-
C.
\(5 < \sqrt {50} - 2\)
-
D.
Chưa đủ điều kiện để so sánh.
Đáp án : C
So sánh hai căn bậc hai: Với hai số \(a,b\) không âm ta có \(a < b \Leftrightarrow \sqrt a < \sqrt b \).
Tách \(5 = 7 - 2 = \sqrt {49} - 2\).
Vì \(49 < 50 \) nên \( \sqrt {49} < \sqrt {50} \)
\( 7 < \sqrt {50} \)
\(7 - 2 < \sqrt {50} - 2 \)
\( 5 < \sqrt {50} - 2\).
Không giải phương trình, tính tổng hai nghiệm (nếu có) của phương trình \( - 3{x^2} + 5x + 1 = 0\).
-
A.
\( - \dfrac{5}{6}\)
-
B.
\(\dfrac{5}{6}\)
-
C.
\( - \dfrac{5}{3}\)
-
D.
\(\dfrac{5}{3}\)
Đáp án : D
Nếu \({x_1},{x_2}\) là hai nghiệm của phương trình \(a{x^2} + bx + c = 0\,\,(a \ne 0)\) thì \(\left\{ \begin{array}{l}{x_1} + {x_2} = \dfrac{{ - b}}{a}\\{x_1} \cdot {x_2} = \dfrac{c}{a}\end{array} \right..\)
Phương trình \( - 3{x^2} + 5x + 1 = 0\) có \(\Delta = {5^2} - 4.1.\left( { - 3} \right) = 37 > 0\) nên phương trình có hai nghiệm \({x_1};{x_2}\)
Theo định lí Vieftee, ta có \({x_1} + {x_2} = - \dfrac{5}{{ - 3}}= \dfrac{5}{3}\).
Rút gọn biểu thức \(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) với \(a > 0\) ta được:
-
A.
\(\dfrac{{47}}{{10}}\sqrt a \)
-
B.
\(\dfrac{{21}}{5}\sqrt a \)
-
C.
\(\dfrac{{47}}{{10}}\sqrt {2a} \)
-
D.
\(\dfrac{{47}}{5}\sqrt {2a} \)
Đáp án : C
- Khử mẫu biểu thức lấy căn theo công thức \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt {AB} }}{B}\,\left( {A \ge 0,B > 0} \right)\)
- Sử dụng công thức khai phương một thương \(\sqrt {\dfrac{A}{B}} = \dfrac{{\sqrt A }}{{\sqrt B }}\) với \(A \ge 0,B > 0\) và công thức khai phương một tích \(\sqrt {AB} = \sqrt A .\sqrt B ,\,\,\left( {A,B \ge 0} \right)\)
- Cộng trừ các căn thức bậc hai.
\(3\sqrt {8a} + \dfrac{1}{4}\sqrt {\dfrac{{32a}}{{25}}} - \dfrac{a}{{\sqrt 3 }}.\sqrt {\dfrac{3}{{2a}}} - \sqrt {2a} \) \( = 3\sqrt {4.2a} + \dfrac{1}{4}\dfrac{{\sqrt {16.2a} }}{{\sqrt {25} }} - \dfrac{a}{{\sqrt 3 }}.\dfrac{{\sqrt 3 }}{{\sqrt {2a} }} - \sqrt {2a} \) \( = 3.2\sqrt {2a} + \dfrac{1}{4}.\dfrac{{4\sqrt {2a} }}{5} - \dfrac{a}{{\sqrt 3 }}.\dfrac{{\sqrt 3 .\sqrt {2a} }}{{2a}} - \sqrt {2a} \) \( = 6\sqrt {2a} + \dfrac{1}{5}\sqrt {2a} - \dfrac{1}{2}\sqrt {2a} - \sqrt {2a} \)
\( = \sqrt {2a} .\left( {6 + \dfrac{1}{5} - \dfrac{1}{2} - 1} \right) = \dfrac{{47}}{{10}}\sqrt {2a} \)
Cho hình vẽ dưới đây, góc \(DIE\) có số đo bằng
-
A.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
-
B.
$\dfrac{1}{2}$(sđ \(\overparen{DmE} - \) sđ \(\overparen{CnF}\) )
-
C.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
-
D.
$\dfrac{1}{2}$(sđ \(\overparen{DF} + \) sđ \(\overparen{CE}\) )
Đáp án : A
Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
\(\widehat {DIE} = \)$\dfrac{1}{2}$(sđ \(\overparen{DmE} + \) sđ \(\overparen{CnF}\) )
Hàm số nào sau đây là hàm số đồng biến?
-
A.
\(y = - \left( {\dfrac{x}{2} - 3} \right)\)
-
B.
\(y = \dfrac{{\sqrt 3 }}{2}\left( {x + 1} \right)\)
-
C.
\(y = - 5 - 3x\)
-
D.
\(y = - \left( {9 + 3x} \right)\)
Đáp án : B
Hàm số bậc nhất \(y = ax + b\) \(\left( {a \ne 0} \right)\)xác định với mọi giá trị của \(x\) thuộc \(\mathbb{R}\)và có tính chất sau
- Đồng biến trên \(\mathbb{R}\) nếu \(a > 0\).
- Nghịch biến trên \(\mathbb{R}\) nếu \(a < 0\).
Hàm số \(y = - \left( {\dfrac{x}{2} - 3} \right)\)\( \Leftrightarrow y = - \dfrac{1}{2}x + 3\) có \(a = - \dfrac{1}{2} < 0\) nên là hàm số nghịch biến
Hàm số \(y = \dfrac{{\sqrt 3 }}{2}\left( {x + 1} \right)\)\( \Leftrightarrow y = \dfrac{{\sqrt 3 }}{2}x + \dfrac{{\sqrt 3 }}{2}\) có \(a = \dfrac{{\sqrt 3 }}{2} > 0\) nên là hàm số đồng biến
Hàm số \(y = - 5 - 3x\)\( \Leftrightarrow y = x - 9\)có \(a = - 1 < 0\) nên là hàm số nghịch biến.
Hàm số \(y = - \left( {9 + 3x} \right) \Leftrightarrow y = - 9 - 3x\) có \(a = - 3 < 0\) nên là hàm số nghịch biến.
Hệ phương trình \(\left\{ \begin{array}{l}{x^2} = 3x - y\\{y^2} = 3y - x\end{array} \right.\) có bao nhiêu cặp nghiệm \(\left( {x;y} \right)\) ?
-
A.
\(1.\)
-
B.
\(2.\)
-
C.
\(3.\)
-
D.
\(4.\)
Đáp án : B
Giải hệ phương trình đối xứng loại 2
+ Trừ vế với vế của hai phương trình ta được phương trình mới
+ Biến đổi phương trình nhận được và kết hợp với một trong hai phương trình ban đầu ta tìm được \(x;y\) .
Ta có : \(\left\{ \begin{array}{l}{x^2} = 3x - y\\{y^2} = 3y - x\end{array} \right.\)\( \Rightarrow {x^2} - {y^2} = 4x - 4y\)\( \Rightarrow \left( {x - y} \right)\left( {x + y} \right) - 4\left( {x - y} \right) = 0 \Leftrightarrow \left( {x - y} \right)\left( {x + y - 4} \right) = 0\) \( \Leftrightarrow \left[ \begin{array}{l}x - y = 0\\x + y - 4 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = y\\y = 4 - x\end{array} \right.\)
Khi \(x = y\) thì \({x^2} - 2x = 0 \Leftrightarrow x = 0;x = 2\)
Khi \(y = 4 - x\) thì \({x^2} - 4x + 4 = 0\) \( \Leftrightarrow x = 2\)
Vậy hệ phương trình có 2 nghiệm \(\left( {0;0} \right),\left( {2;2} \right)\).
Tập nghiệm của phương trình \(\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}} = 2\) là:
-
A.
\(S = \left\{ {1; - 7} \right\}\)
-
B.
\(S = \left\{ { - 1;7} \right\}\)
-
C.
\(S = \left\{ 7 \right\}\)
-
D.
\(S = \left\{ { - 1} \right\}\)
Đáp án : B
- Áp dụng \(\sqrt[3]{x} + \sqrt[3]{y} = {\left( {\sqrt[3]{x} + \sqrt[3]{y}} \right)^3} = x + y + 3\sqrt[3]{{xy}}\left( {\sqrt x + \sqrt y } \right)\)
-Lập phương hai vế, sau đó biến đổi để đưa về dạng cơ bản \(\sqrt[3]{x} = a \) thì \(x = {a^3}\)
Ta có: \(\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}} = 2\)
\( {\left( {\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}}} \right)^3} = {2^3}\)
\( x + 1 + 7 - x + 3\sqrt[3]{{\left( {x + 1} \right)\left( {7 - x} \right)}}\left( {\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}}} \right) = 8\)
Mà \(\sqrt[3]{{x + 1}} + \sqrt[3]{{7 - x}} = 2\) nên ta có phương trình
\(3\sqrt[3]{{\left( {x + 1} \right)\left( {7 - x} \right)}}. 2 + 8 = 8\\ 6\sqrt[3]{{\left( {x + 1} \right)\left( {7 - x} \right)}} = 0\)
\( \sqrt[3]{{\left( {x + 1} \right)\left( {7 - x} \right)}} = 0 \\ \left( {x + 1} \right)\left( {7 - x} \right) = 0 \\ \left[ \begin{array}{l}x + 1 = 0\\7 - x = 0\end{array} \right. \\ \left[ \begin{array}{l}x = - 1\\x = 7\end{array} \right.\)
Tập nghiệm của phương trình là \(S = \left\{ { - 1;7} \right\}\).
Chọn khẳng định đúng. Góc ở tâm là góc
-
A.
Có đỉnh nằm trên đường tròn
-
B.
Có đỉnh trùng với tâm đường tròn
-
C.
Có hai cạnh là hai đường kính của đường tròn
-
D.
Có đỉnh nằm trên bán kính của đường tròn
Đáp án : B
Góc có đỉnh trùng với tâm đường tròn được gọi là góc ở tâm.
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi:
-
A.
\(m \notin \left\{ {0;\dfrac{1}{2}} \right\}\)
-
B.
\(m > 0\)
-
C.
\(m \ne 0\)
-
D.
\(m \ne \dfrac{1}{2}\)
Đáp án : A
Sử dụng định nghĩa hàm số bậc nhất
Hàm số bậc nhất là hàm số dạng \(y = ax + b\,\,\left( {a \ne 0} \right)\)
Hàm số \(y = \dfrac{{3m}}{{1 - 2m}}x - 5\) là hàm số bậc nhất khi \(\left\{ \begin{array}{l}\dfrac{{3m}}{{1 - 2m}} \ne 0\\1 - 2m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3m \ne 0\\2m \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne \dfrac{1}{2}\end{array} \right.\)
Cho hàm số \(y = f\left( x \right) = \dfrac{1}{2}{x^2}\) . Tổng các giá trị của \(a\) thỏa mãn \(f\left( a \right) = 3 + \sqrt 5 \) là
-
A.
\(1\)
-
B.
\(2\sqrt 5 \)
-
C.
\(0\)
-
D.
\( - 2\)
Đáp án : C
Giá trị của hàm số \(y = a{x^2}\left( {a \ne 0} \right)\) tại điểm \(x = {x_0}\) là \({y_0} = a{x_o}^2\).
Sử dụng hằng đẳng thực bình phương của một tổng để tính.
Ta có \(f\left( a \right) = 3 + \sqrt 5 \)
hay \(\dfrac{1}{2}{a^2} = 3 + \sqrt 5 \)
\({a^2} = 6 + 2\sqrt 5 \)
\({a^2} =5 +2\sqrt 5.1 + 1\)
\({a^2} =(\sqrt 5)^2+2\sqrt 5.1+1^2\)
\({a^2} = {\left( {\sqrt 5 + 1} \right)^2}\)
Suy ra \(a = \sqrt 5 + 1\) hoặc \(a = - \sqrt 5 - 1\)
Vậy tổng các giá trị của \(a\) là \(\left( {\sqrt 5 + 1} \right) + \left( { - \sqrt 5 - 1} \right) = 0\)
Viết phương trình đường thẳng \(d\) biết \(d\) tạo với đường thẳng \(y = 2\) (theo chiều dương) một góc bằng \(135^\circ \) và cắt trục tung tại điểm có tung độ bằng \(4\).
-
A.
\(y = x - 4\)
-
B.
\(y = - x - 4\)
-
C.
\(y = x + 4\)
-
D.
\(y = - x + 4\)
Đáp án : D
Gọi phương trình đường thẳng \(d:y = ax + b\) \(\left( {a \ne 0} \right)\)
Xác định hệ số \(a\) dựa vào góc tạo bởi đường thẳng \(d\) với đường thẳng cho trước tìm \(b\) dựa vào giao điểm với trục tung.
Gọi phương trình đường thẳng \(d:y = ax + b\,\,\left( {a \ne 0} \right)\)
Vì góc tạo bởi đường thẳng \(d\) và đường thẳng \(y = 2\) là \(135^\circ \) nên góc tạo bởi đường thẳng \(d\) và trục \(Ox\) cũng là \(135^\circ \)(do đường thẳng \(y = 1\) song song với trục \(Ox\)) nên \(a = \tan 135^\circ = - 1\)
\( \Rightarrow y = - x + b\)
Vì đường thẳng \(d\) cắt trục tung tại điểm có tung độ \(4\) nên \(b = 4\).
Từ đó \(d:y = - x + 4\).
Phép tính \(\sqrt {{{12}^2}.{{\left( { - 11} \right)}^2}} \) có kết quả là?
-
A.
\( - 33\)
-
B.
\( - 132\)
-
C.
\(132\)
-
D.
Không tồn tại.
Đáp án : C
- Sử dụng công thức khai phương một tích: Với hai số \(a,b\) không âm, ta có \(\sqrt a .\sqrt b = \sqrt {ab} \)
- Sử dụng hằng đẳng thức: \(\sqrt {{A^2}} = \left| A \right|\)
\(\sqrt {{{12}^2}.{{\left( { - 11} \right)}^2}} = \sqrt {{{12}^2}} .\sqrt {{{\left( { - 11} \right)}^2}} = \left| {12} \right|.\left| { - 11} \right| = 12.11 = 132\).
Cho hai số tự nhiên biết rằng số thứ nhất lớn hơn hai lần số thứ hai là \(3\) và hiệu các bình phương của chúng bằng \(360\) . Tìm số bé hơn.
-
A.
\(12\)
-
B.
\(10\)
-
C.
\(21\)
-
D.
\(9\)
Đáp án : D
Gọi số thứ nhất là $a;a \in {\mathbb{N}}$ ; số thứ hai là $b;b \in {\mathbb{N}}.$
Vì số thứ nhất lớn hơn hai lần số thứ hai là \(3\) nên ta biểu diễn được b theo a.
Vì hiệu các bình phương của chúng bằng \(360\) nên ta viết được phương trình theo a.
Tính \(\Delta '\) để tìm a, từ đó ta tính được b.
Gọi số thứ nhất là \(a;a \in {\mathbb{N}^*}\) ; số thứ hai là \(b;b \in {\mathbb{N}^*}\)
Giả sử \(a > b.\)
Vì số thứ nhất lớn hơn hai lần số thứ hai là \(3\) nên ta có \(a - 2b = 3\) hay \(a = 2b + 3\)
Vì hiệu các bình phương của chúng bằng \(360\) nên ta có phương trình: \({a^2} - {b^2} = 360\,\,\left( * \right)\)
Thay \(a = 2b + 3\) vào (*) ta được \({\left( {2b + 3} \right)^2} - {b^2} = 360\) hay \(3{b^2} + 12b - 351 = 0\)
Ta có \(\Delta ' = 1089\) suy ra \( \sqrt {\Delta '} = 33\) nên \(b_1 = \dfrac{{ - 6 + 33}}{3} = 9\left( {tm} \right)\); \(b_2 = \dfrac{{ - 6 - 33}}{3} = - 13\left( {ktm} \right)\)
Với \(b = 9\) thì \(a = 2.9 + 3 = 21\)
Vậy số bé hơn là \(9\) .
Cho tam giác \(ABC\) vuông tại \(A\) có \(AC = 7\,cm,AB = \,5cm\). Tính $BC;\widehat C$ .
-
A.
$BC = \sqrt {74} (cm);\widehat C \approx 35^\circ 32'$
-
B.
$BC = \sqrt {74} (cm);\widehat C \approx 36^\circ 32'$
-
C.
$BC = \sqrt {74} (cm) ;\widehat C \approx 35^\circ 33'$
-
D.
$BC = \sqrt {75} (cm) ;\widehat C \approx 35^\circ 32'$
Đáp án : A
+) Tính cạnh còn lại theo định lý Py-ta-go
+) Tìm tỉ số lượng giác của góc từ đó suy ra góc.
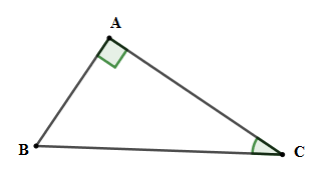
Xét tam giác \(ABC\) vuông tại \(A\) có
+) $B{C^2} = A{B^2} + A{C^2} = {5^2} + {7^2} = 74 \Rightarrow BC = \sqrt {74} (cm)$
+) $\tan C = \dfrac{{AB}}{{AC}} = \dfrac{5}{7} \Rightarrow \widehat C \approx 35^\circ 32'$
Vậy $BC = \sqrt {74}(cm) ;\widehat C \approx 35^\circ 32'$.
Cho tam giác \(ABC\) có các đường cao \(BD,CE\) . Chọn khẳng định đúng.
-
A.
Bốn điểm \(B,E,D,C\) cùng nằm trên một đường tròn
-
B.
Năm điểm \(A,B,E,D,C\) cùng nằm trên một đường tròn
-
C.
Cả A, B đều sai
-
D.
Cả A, B đều đúng
Đáp án : A
Sử dụng: Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
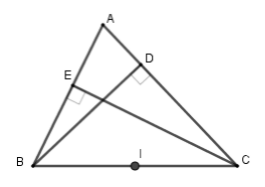
Gọi \(I\) là trung điểm của \(BC\).
Xét tam giác \(BEC\) vuông tại \(E\) có \(EI = IB = IC = \dfrac{{BC}}{2}\) (vì \(EI\) là đường trung tuyến ứng với cạnh huyền)
Xét tam giác \(BDC\) vuông tại \(D\) có \(DI = IB = IC = \dfrac{{BC}}{2}\) (vì \(DI\) là đường trung tuyến ứng với cạnh huyền)
Từ đó ta có \(ID = IE = IB = IC = \dfrac{{BC}}{2}\) nên bốn điểm \(B,E,D,C\) cùng nằm trên một đường tròn có bán kính \(R = \dfrac{{BC}}{2}\).
Ta thấy \(IA > ID\) nên điểm \(A\) không thuộc đường tròn trên.
Phương trình \({(2x + 1)^4}-8{(2x + 1)^2}-9 = 0\) có tổng các nghiệm là
-
A.
\(1\)
-
B.
\( - 2\)
-
C.
\( - 1\)
-
D.
\(2\sqrt 2 \)
Đáp án : C
Giải phương trình trùng phương bằng cách đặt \({\left( {2x + 1} \right)^2} = t\,\left( {t \ge 0} \right)\)
Đưa về giải phương trình bậc hai ẩn \(t\) , so sánh điều kiện \(t \ge 0\) rồi thay lại cách đặt để tìm \(x\).
Đặt \({\left( {2x + 1} \right)^2} = t\,\left( {t \ge 0} \right)\) ta được phương trình \({t^2} - 8t - 9 = 0\) (*)
Ta có \(a - b + c = 1 - \left( { - 8} \right) + \left( { - 9} \right) = 0\) nên phương trình (*) có hai nghiệm \({t_1} = 9\left( {tm} \right);{t_2} = -1\left( {ktm} \right)\)
Thay lại cách đặt ta có \({\left( {2x + 1} \right)^2} = 9 \Leftrightarrow \left[ \begin{array}{l}2x + 1 = 3\\2x + 1 = - 3\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
Suy ra tổng các nghiệm là \(1 + \left( { - 2} \right) = - 1\).
Cho parabol\((P):y = 5{x^2}\) và đường thẳng \((d):y = - 4x - 4\). Số giao điểm của đường thẳng \(d\) và parabol \(\left( P \right)\) là:
-
A.
\(1\)
-
B.
\(0\)
-
C.
\(3\)
-
D.
\(2\)
Đáp án : B
Cho parabol \((P):y = {\rm{a}}{{\rm{x}}^2}(a \ne 0)\) và đường thẳng \(d:y = mx + n\). Để tìm tọa độ giao điểm (nếu có) của \((d)\) và \((P)\), ta làm như sau:
Bước 1. Xét phương trình hoành độ giao điểm của \((d)\) và \((P)\): \({\rm{a}}{{\rm{x}}^2} = mx + n\)
Bước 2. Giải phương trình (*) ta tìm được nghiệm (nếu có). Từ đó suy ra số giao điểm của parabol và đường thẳng
Xét phương trình hoành độ giao điểm của parabol \(\left( P \right)\) và đường thẳng \((d):\)
\(5{x^2} = - 4x - 4 \\ 5{x^2} + 4x + 4 = 0 \\{x^2} + 4{x^2} + 4x + 4 = 0 \\ {x^2} + {\left( {x + 2} \right)^2} = 0\,\,\left( * \right)\)
Xét \({x^2} + {\left( {x + 2} \right)^2} \ge 0;\forall x\) và dấu “=” xảy ra khi \(\left\{ \begin{array}{l}x = 0\\x + 2 = 0\end{array} \right. \) hay \(\left\{ \begin{array}{l}x = 0\\x = - 2\end{array} \right.\) (vô lý) nên \({x^2} + {\left( {x + 2} \right)^2} > 0;\forall x\)
Hay phương trình (*) vô nghiệm.
Vậy không có giao điểm của đường thẳng \((d)\) và parabol \(\left( P \right)\).
Đồ thị hàm số \(y = 5x - \dfrac{2}{5}\) đi qua điểm nào dưới đây?
-
A.
\(A\left( {1;\dfrac{{22}}{5}} \right)\)
-
B.
\(B\left( {\dfrac{1}{5};\dfrac{3}{5}} \right)\)
-
C.
\(C\left( { - \dfrac{2}{{25}}; - \dfrac{3}{5}} \right)\)
-
D.
\(D\left( {2;10} \right)\)
Đáp án : B
Đồ thị hàm số \(y = ax + b(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b\).
Thay tọa độ từng điểm vào hàm số ta được
+) Với \(A\left( {1;\dfrac{{22}}{5}} \right)\). Thay \(x = 1;y = \dfrac{{22}}{5}\) vào \(y = 5x - \dfrac{2}{5}\) ta được \(5.1 - \dfrac{2}{5} = \dfrac{{22}}{5} \Leftrightarrow \dfrac{{23}}{5} = \dfrac{{22}}{5}\) (Vô lý)
+) Với \(B\left( {\dfrac{1}{5};\dfrac{3}{5}} \right)\). Thay \(x = \dfrac{1}{5};y = \dfrac{3}{5}\) vào \(y = 5x - \dfrac{2}{5}\) ta được \(5.\dfrac{1}{5} - \dfrac{2}{5} = 1 - \dfrac{2}{5} = \dfrac{3}{5}\) (Luôn đúng)
+) Với \(C\left( { - \dfrac{2}{{25}}; - \dfrac{3}{5}} \right)\). Thay \(x = - \dfrac{2}{{25}};y = - \dfrac{3}{5}\) vào \(y = 5x - \dfrac{2}{5}\) ta được \(5.\dfrac{{ - 2}}{{25}} - \dfrac{2}{5} = - \dfrac{3}{5} \Leftrightarrow - \dfrac{4}{5} = - \dfrac{3}{5}\) (Vô lý)
+)Với \(D\left( {2;10} \right)\). Thay \(x = 2;y = 10\) vào \(y = 5x - \dfrac{2}{5}\) ta được \(5.2 - \dfrac{2}{5} = 10 \Leftrightarrow \dfrac{{48}}{5} = 10\) (Vô lý)
\( \Rightarrow B\left( {\dfrac{1}{5};\dfrac{3}{5}} \right)\) thuộc đồ thị hàm số \(y = 5x - \dfrac{2}{5}\).
Cho một hình cầu và một hình lập phương ngoại tiếp nó. Nếu diện tích diện tích toàn phần của hình lập phương là \(24c{m^2}\) thì diện tích mặt cầu là:
-
A.
\(4\pi \)
-
B.
\(4\)
-
C.
\(2\pi \)
-
D.
\(2\)
Đáp án : A
Sử dụng công thức diện tích mặt cầu \(S = 4\pi {R^2}\) và diện tích toàn phần của hình lập phương \({S_{tp}} = 6{a^2}\) với \(a\) là độ dài cạnh của hình lập phương.
Vì hình cầu nội tiếp hình lập phương nên bán kính hình cầu \(R = \dfrac{a}{2}\) với \(a\) là cạnh hình lập phương.
Diện tích toàn phần của hình lập phương là:
\({S_{tp}} = 6{a^2} = 24 \)
Suy ra \(a = 2cm\)
Do đó \(R = \dfrac{2}{2} = 1cm\)
Khi đó ta có diện tích mặt cầu là:
\(S = 4\pi {R^2} = 4\pi {.1^2} = 4\pi \left( {c{m^2}} \right)\)
Phương trình \(\sqrt {{x^2} - 2x + 10} + \sqrt {6{x^2} - 12x + 31} = 8\) có nghiệm là
-
A.
Số lẻ dương
-
B.
Số chẵn dương
-
C.
Số lẻ âm
-
D.
Số vô tỉ
Đáp án : A
Ta có \(\sqrt {{x^2} - 2x + 10} + \sqrt {6{x^2} - 12x + 31} = 8\)\( \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + 9} + \sqrt {6{{\left( {x - 1} \right)}^2} + 25} = 8\)
Nhận thấy \(\sqrt {{{\left( {x - 1} \right)}^2} + 9} \ge 3;\sqrt {6{{\left( {x - 1} \right)}^2} + 25} \ge 5\) nên \(\sqrt {{{\left( {x - 1} \right)}^2} + 9} + \sqrt {6{{\left( {x - 1} \right)}^2} + 25} \ge 3 + 5\)
\( \Leftrightarrow \sqrt {{{\left( {x - 1} \right)}^2} + 9} + \sqrt {6{{\left( {x - 1} \right)}^2} + 25} \ge 8\)
Dấu “=” xảy ra khi \(\left\{ \begin{array}{l}\sqrt {{{\left( {x - 1} \right)}^2} + 9} = 3\\\sqrt {6{{\left( {x - 1} \right)}^2} + 25} = 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x - 1 = 0\\x - 1 = 0\end{array} \right. \Rightarrow x = 1\)
Vậy phương trình đã cho có nghiệm duy nhất \(x = 1.\)
Một cột đèn điện \(AB\) cao \(7m\) có bóng in trên mặt đất là \(AC\) dài \(4m.\) Hãy tính góc \(\widehat {BCA}\) (làm tròn đến phút) mà tia sáng mặt trời tạo với mặt đất.
-
A.
\(59^\circ 45'\)
-
B.
\(62^\circ \)
-
C.
\(61^\circ 15'\)
-
D.
\(60^\circ 15'\)
Đáp án : D
Sử dụng tỉ số lượng giác của góc nhọn từ đó suy ra góc.
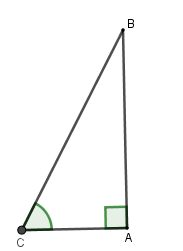
Ta có \(\tan C = \dfrac{{AB}}{{AC}} = \dfrac{7}{4} \Rightarrow \widehat C \simeq 60^\circ 15'\)
Hộp sữa ông Thọ có dạng hình trụ (đã bỏ nắp) có chiều cao \(h = 10cm\) và đường kính đáy là \(d= 6cm\) . Tính diện tích các mặt của hộp sữa. Lấy \(\pi \approx 3,14\)
-
A.
\(110\pi \,\left( {c{m^2}} \right)\)
-
B.
\(129\pi \,\left( {c{m^2}} \right)\)
-
C.
\(96\pi \,\left( {c{m^2}} \right)\)
-
D.
\(69\pi \,\left( {c{m^2}} \right)\)
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình trụ \({S_{xq}} = 2\pi Rh\) và diện tích một đáy
Bán kính đường tròn đáy \(R = \dfrac{6}{2} = 3\,cm\) nên diện tích một đáy là \(S_đ=\pi.R^2=9\pi\,(cm^2)\)
Ta có diện tích xung quanh của hình trụ:
\({S_{xq}} = 2\pi Rh = 2\pi .3.10 = 60\pi \,c{m^2}\)
Vì hộp sữa đã mất nắp nên diện tích các mặt của hộp sữa là:
\({S_{tp}} = 9\pi + 60\pi = 69\pi \,\left( {c{m^2}} \right)\)
Một phòng họp có 360 ghế ngồi được xếp thành từng dãy và số ghế của từng dãy đều như nhau. Nếu số dãy tăng thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400 ghế. Hỏi trong phòng họp có bao nhiêu dãy ghế (biết số dãy ghế ít hơn 20).
-
A.
14 dãy
-
B.
15 dãy
-
C.
16 dãy
-
D.
17 dãy
Đáp án : B
Các bước giải bài toán bằng cách lập phương trình:
+ Chọn ẩn và đặt điều kiện cho ẩn
+ Biểu thị các đại lượng chưa biết qua ẩn và các đại lượng đã biết.
+ Lập phương trình - giải phương trình.
+ Chọn kết quả và trả lời.
Gọi số dãy ghế là x \((x \in N*)\) (dãy)
Số ghế ở mỗi dãy là: \(\dfrac{{360}}{x}\) (ghế)
Số dãy ghế lúc sau là: \(x + 1\) (dãy)
Số ghế ở mỗi dãy lúc sau là: \(\dfrac{{360}}{x} + 1\) (ghế)
Vì sau khi tăng số dãy tăng thêm 1 và số ghế của mỗi dãy tăng thêm 1 thì trong phòng có 400 ghế nên ta có phương trình:
\(\begin{array}{l}(x + 1)\left( {\dfrac{{360}}{x} + 1} \right) = 400\\ (x + 1)\left( {\dfrac{{360 + x}}{x}} \right) = 400\\(x + 1)(360 + x) = 400x\\ 360x + {x^2} + 360 + x = 400x\\ {x^2} - 39x + 360 = 0\end{array}\)
Ta có: \(\Delta = {( - 39)^2} - 4.1.360 = 81 > 0\) nên phương trình có 2 nghiệm phân biệt: \({x_1} = \dfrac{{39 + \sqrt {81} }}{2} = 24\,\,\,\,(ktm)\) và \({x_2} = \dfrac{{39 - \sqrt {81} }}{2} = 15\,\,\,\,(tm)\)
Vậy số dãy ghế là 15 (dãy).
Thu gọn $\sqrt[3]{{125{a^3}}}$ ta được
-
A.
$25a$
-
B.
$5a$
-
C.
$ - 25{a^3}$
-
D.
$ - 5a$
Đáp án : B
Sử dụng công thức $\sqrt[3]{{{a^3}}} = a$
Ta có $\sqrt[3]{{125{a^3}}} = \sqrt[3]{{{{\left( {5a} \right)}^3}}} = 5a$
Không dùng bảng số và máy tính, hãy so sánh \(\cot 50^\circ \) và \(\cot 46^\circ \)
-
A.
\(\cot 46^\circ = \cot 50^\circ \)
-
B.
\(\cot 46^\circ > \cot 50^\circ \)
-
C.
\(\cot 46^\circ < \cot 50^\circ \)
-
D.
\(\cot 46^\circ \ge \cot 50^\circ \)
Đáp án : B
Sử dụng nhận xét : Với góc nhọn \(\alpha ,\,\beta ,\) ta có: \(\alpha < \beta \Leftrightarrow \cot \alpha > \cot \beta \)
Vì \(46^\circ < 50^\circ \Leftrightarrow \cot 46^\circ > \cot 50^\circ \).
Cho đường thẳng \(d\):\(y = \dfrac{1}{3}x - 10\). Hệ số góc của đường thẳng \(d\) là
-
A.
\(3\)
-
B.
\(\dfrac{1}{3}\)
-
C.
\( - \dfrac{1}{3}\)
-
D.
\( - 3\)
Đáp án : B
Sử dụng lý thuyết về hệ số góc của đường thẳng.
Đường thẳng \(d\) có phương trình \(y = ax + b\,\left( {a \ne 0} \right)\)có \(a\) là hệ số góc.
Đường thẳng \(d\):\(y = \dfrac{1}{3}x - 10\) có hệ số góc là \(a = \dfrac{1}{3}\).
Cho hai vòi nước cùng lúc chảy vào một bể cạn. Nếu chảy riêng từng vòi thì vòi thứ nhất chảy đầy bể chậm hơn vòi thứ hai \(2\) giờ. Khi nước đầy bể, người ta khóa vòi thứ nhất và vòi thứ hai lại, đồng thời mở vòi thứ ba cho nước chảy ra thì sau \(7,5\) giờ bể cạn nước. Khi nước trong bể đã cạn mở cả ba vòi thì sau \(20\) giờ bể lại đầy nước. Hỏi nếu chỉ dùng vòi thứ nhất thì sau bao lâu bể đầy nước?
-
A.
\(9\) giờ
-
B.
\(12\) giờ
-
C.
\(10\) giờ
-
D.
\(8\) giờ
Đáp án : C
Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là \(x\) (giờ), \(\left( {x > 2} \right)\).
Biểu diễn tốc độ chảy của các vòi trong một giờ.
Lập phương trình.
Giải phương trình để tìm x.
Gọi thời gian mà vòi thứ nhất chảy riêng đầy bể là \(x\) (giờ), \(\left( {x > 2} \right)\).
Trong một giờ:
- Vòi thứ nhất chảy được \(\dfrac{1}{x}\) ( bể).
- Vòi thứ hai chảy được \(\dfrac{1}{{x - 2}}\) ( bể).
- Vì vòi thứ ba chảy ra trong 7,5 giờ thì cạn bề nên trong 1h vòi thứ ba chảy được \(\dfrac{2}{{15}}\) ( bể).
Khi mở cả ba vòi thì vòi thứ nhất và vòi thứ hai chảy vào bể còn vòi thứ ba cho nước ở bể chảy ra nên ta có phương trình:
\(\dfrac{1}{x} + \dfrac{1}{{x - 2}} - \dfrac{2}{{15}} = \dfrac{1}{{20}}\)
\(\dfrac{1}{x} + \dfrac{1}{{x - 2}} = \dfrac{{11}}{{60}}\)
\(\dfrac{{x - 2 + x}}{{x\left( {x - 2} \right)}} = \dfrac{{11}}{{60}}\)
\(\dfrac{{2x - 2}}{{{x^2} - 2x}} = \dfrac{{11}}{{60}}\)
\(120x - 120 = 11{x^2} - 22x\)
\(11{x^2} - 142x + 120 = 0\)
Ta có \(\Delta ' = 3721 > 0\) suy ra \(\sqrt {\Delta '} = 61\) nên phương trình có hai nghiệm phân biệt \(x_1 = \dfrac{{71 - 61}}{{11}} = \dfrac{{10}}{{11}}\left( {ktm} \right)\) và \(x_2 = \dfrac{{71 + 61}}{{11}} = 12\left( {tm} \right)\)
Vậy chỉ dùng vòi thứ nhất thì sau \(10\) giờ bể đầy nước.
Phát biểu nào sau đây đúng nhất
-
A.
Mỗi tam giác luôn có một đường tròn ngoại tiếp
-
B.
Mỗi tứ giác luôn có một đường tròn nội tiếp
-
C.
Cả A và B đều đúng
-
D.
Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác là đường tròn nội tiếp tam giác đó
Đáp án : A
Mỗi tam giác luôn có một và chỉ một đường tròn ngoại tiếp ⇒ Câu A đúng
Không phải tứ giác nào cũng có đường tròn nội tiếp ⇒ Câu B sai
Đường tròn tiếp xúc với các đường thẳng chứa các cạnh của tam giác không phải lúc nào cũng là đường tròn nội tiếp tam giác (mà có thể là đường tròn bàng tiếp) ⇒ Câu D sai
Tính \(x\) trong hình vẽ sau:
-
A.
\(x = 14\)
-
B.
\(x = 13\)
-
C.
\(x = 12\)
-
D.
\(x = \sqrt {145} \)
Đáp án : C
Tính \(x\) theo hệ thức lượng \(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có:
\(\dfrac{1}{{A{H^2}}} = \dfrac{1}{{A{B^2}}} + \dfrac{1}{{A{C^2}}}\)\( \Rightarrow AH = \dfrac{{AB.AC}}{{\sqrt {A{B^2} + A{C^2}} }} = \dfrac{{15.20}}{{\sqrt {{{15}^2} + {{20}^2}} }} = 12\)
Vậy \(x = 12\).
Cho hai hàm số \(f\left( x \right) = 6{x^4}\) và \(h\left( x \right) = 7 - \dfrac{{3.x}}{2}\). So sánh \(f\left( { - 1} \right)\) và \(h\left( {\dfrac{2}{3}} \right)\)
-
A.
\(f\left( { - 1} \right) = h\left( {\dfrac{2}{3}} \right)\)
-
B.
\(f\left( { - 1} \right) > h\left( {\dfrac{2}{3}} \right)\)
-
C.
\(f\left( { - 1} \right) < h\left( {\dfrac{2}{3}} \right)\)
-
D.
Không đủ điều kiện so sánh
Đáp án : A
Sử dụng cách tính giá trị hàm số tại một điểm
Để tính giá trị \({y_0}\) của hàm số \(y = f\left( x \right)\) tại điểm \({x_0}\) ta thay \(x = {x_0}\) vào \(f\left( x \right)\), ta được \({y_0} = f\left( {{x_0}} \right)\).
So sánh các giá trị tìm được
Thay \(x = - 1\) vào hàm số \(f\left( x \right) = 6{x^4}\) ta được \(f\left( { - 1} \right) = 6.{\left( { - 1} \right)^4} = 6\).
Thay \(x = \dfrac{2}{3}\) vào hàm số \(h\left( x \right) = 7 - \dfrac{{3x}}{2}\) ta được \(h\left( {\dfrac{2}{3}} \right) = 7 - \dfrac{{3.\dfrac{2}{3}}}{2} = 6\).
Nên \(f\left( { - 1} \right) = h\left( {\dfrac{2}{3}} \right)\).
Tìm \(m\) để hai phương trình \({x^2} + mx + 2 = 0\) và \({x^2} + 2x + m = 0\) có ít nhất một nghiệm chung.
-
A.
\(1\)
-
B.
\( - 3\)
-
C.
\( - 1\)
-
D.
\(3\)
Đáp án : B
Hai phương trình có nghiệm chung thì nghiệm chung đó phải thoả mãn cả hai phương trình
Gọi \({x_0}\) là nghiệm chung của hai phương trình thì \({x_0}\) phải thỏa mãn hai phương trình trên.
Thay \(x = {x_0}\) vào hai phương trình trên ta được \(\left\{ \begin{array}{l}{x_0}^2 + m{x_0} + 2 = 0\\{x_0}^2 + 2{x_0} + m = 0\end{array} \right. \) \(\Rightarrow (m - 2){x_0} + 2 - m = 0\) \(\Leftrightarrow (m - 2)(x_0-1)= 0\)
+) Nếu \(m = 2\) thì \(0 = 0\) (luôn đúng) hay hai phương trình trùng nhau.
Lúc này phương trình \({x^2} + 2x + 2 = 0 \Leftrightarrow {\left( {x + 1} \right)^2} = - 1\) vô nghiệm nên cả hai phương trình đều vô nghiệm.
Vậy \(m = 2\) không thỏa mãn.
+) Nếu \(m \ne 2\) thì \({x_0} = 1\).
Thay \({x_0} = 1\) vào phương trình \({x_0}^2 + m{x_0} + 2 = 0\) ta được \(1 + m + 2 = 0 \Leftrightarrow m = - 3\).
Vậy \(m = - 3\) thì hai phương trình có nghiệm chung.
Tìm cặp giá trị \((m;n)\) để hai hệ phương trình sau tương đương \(\left\{ \begin{array}{l}3x + 3y = 3\\x + \dfrac{1}{3}y = \dfrac{1}{3}\end{array} \right.(I)\) và
$\left\{ \begin{array}{l}{\rm{x}} - ny = 1\\3mx + my = 1\end{array} \right.(II)$
-
A.
\(\left( {1;\dfrac{1}{2}} \right)\)
-
B.
\(\left( 1;-1 \right)\)
-
C.
\(( - 1;1)\)
-
D.
\(\left( {\dfrac{1}{2}; - 1} \right)\)
Đáp án : B
Giải hệ phương trình (I) sau đó thay nghiệm tìm được vào hệ phương trình (II) để tìm \(m.\)
Giải hệ phương trình (I) \( \Leftrightarrow \left\{ \begin{array}{l}3x + 3y = 3\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3x + 3y - \left( {3x + y} \right) = 3 - 1\\3x + y = 1\end{array} \right.\) \(\left\{ \begin{array}{l}2y = 2\\3x + y = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\3x + 1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 1\\x = 0\end{array} \right.\)
Hai phương trình tương đương \( \Leftrightarrow \) hai phương trình có cùng tập nghiệm hay (0; 1) cũng là nghiệm của phương trình (II).
Thay \(\left\{ \begin{array}{l}x = 0\\y = 1\end{array} \right.\) vào hệ phương trình (II) ta được \(\left\{ \begin{array}{l}0 - n.1 = 1\\0 + m.1 = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}n = - 1\\m = 1\end{array} \right.\)
Vậy \(n = - 1;m =1\).
Rút gọn biểu thức sau \(\sqrt {{{\left( {5 - \sqrt {11} } \right)}^2}} + \sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} \).
-
A.
\(2 + 2\sqrt {11} \)
-
B.
\(8\)
-
C.
\(2\)
-
D.
\(2\sqrt {11} \)
Đáp án : C
+ Sử dụng hằng đẳng thức \(\sqrt {{A^2}} = \left| A \right|\)
+ So sánh hai căn bậc hai \(\sqrt A > \sqrt B \Leftrightarrow A > B\) với \(A,B\) không âm để phá dấu giá trị tuyệt đối.
Ta có: \(\sqrt {{{\left( {5 - \sqrt {11} } \right)}^2}} + \sqrt {{{\left( {3 - \sqrt {11} } \right)}^2}} = \left| {5 - \sqrt {11} } \right| + \left| {3 - \sqrt {11} } \right|\)
Vì:
+) \(5 = \sqrt {25} > \sqrt {11} \) nên \(5 - \sqrt {11} > 0 \), do đó \(\left| {5 - \sqrt {11} } \right| = 5 - \sqrt {11} \)
+) \(3 = \sqrt 9 < \sqrt {11} \) nên \( 3 - \sqrt {11} < 0 \), do đó \( \left| {3 - \sqrt {11} } \right| = \sqrt {11} - 3\)
Vì vậy
\(\sqrt {{{\left( {5 - \sqrt {11} } \right)}^2}} + \sqrt {{{\left( {\sqrt {11} - 3} \right)}^2}} = \left| {5 - \sqrt {11} } \right| + \left| {\sqrt {11} - 3} \right|\)\( = 5 - \sqrt {11} + \sqrt {11} - 3 = 2\).
Đưa thừa số \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \) (\(x < 0\)) vào trong dấu căn ta được:
-
A.
\(\sqrt {\dfrac{{300}}{x}} \)
-
B.
\(\sqrt {\dfrac{{ - 300}}{x}} \)
-
C.
\( - \sqrt {\dfrac{{ - 300}}{x}} \)
-
D.
\( - \sqrt {\dfrac{{ - 60}}{x}} \)
Đáp án : C
Đưa thừa số vào trong dấu căn
+) \(A\sqrt B = \sqrt {{A^2}B} \) với \(A \ge 0\) và \(B \ge 0\)
+) \(A\sqrt B = - \sqrt {{A^2}B} \) với \(A < 0\) và \(B \ge 0\)
Ta có: \(5x\sqrt {\dfrac{{ - 12}}{{{x^3}}}} \)\( = - \sqrt {{{\left( {5x} \right)}^2}.\dfrac{{ - 12}}{{{x^3}}}} = \sqrt {25{x^2}\left( {\dfrac{{ - 12}}{x^3}} \right)} = - \sqrt {\dfrac{{ - 300}}{x}} \).
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt các đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt các đường thẳng AB tại I. Chọn đáp án đúng.
-
A.
Các tam giác $FNI,{\rm{ }}INE$ cân
-
B.
$\widehat {IEN} = 2\widehat {NDC}$
-
C.
$\widehat {DNI} = 3\widehat {DCN}$
-
D.
Tất cả các câu đều sai
Đáp án : A
+) Nhận biết được góc có đỉnh nằm trong, ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm trong, ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn, mối uan hệ giữa số đo cung và dây cung
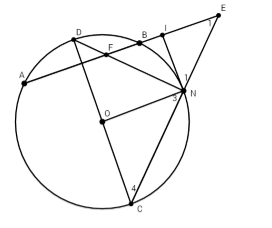
Ta có tam giác AOB cân tại O nên dễ dàng chỉ ra được $sđ\overparen{AD} = sđ\overparen{DB}$
$\begin{array}{l}\widehat {IFN} = \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{AD}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{BD}} \right)\\ = \dfrac{1}{2}sđ\overparen{DN} = \widehat {INF}\end{array}$
Suy ra tam giác FIN cân tại I
Ta có:
$\begin{array}{l}{\widehat N_1} + \widehat {{N_3}} = {90^0} \Rightarrow {\widehat N_1} + \widehat {{C_4}} = {90^0}\\\widehat {{E_1}} = \dfrac{1}{2}\left( {sđ\overparen{AC} - sđ\overparen{BN}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{BC} - sđ\overparen{CN}} \right) = \dfrac{1}{2}sđ\overparen{NC}\\ \Rightarrow \widehat {{C_4}} + \widehat {{E_1}} = \dfrac{1}{2}sđ\overparen{DN} + \dfrac{1}{2}sđ\overparen{NC} \\= \dfrac{1}{2}sđ\overparen{DC} = {90^0}\\ \Rightarrow \widehat {{E_1}} = \widehat {{N_1}}\end{array}$
Do đó \(\Delta INE\) cân tại I.
Trên một hệ trục toạ độ, vẽ parabol
>> Học trực tuyến Lớp 10 cùng thầy cô giáo giỏi tại Tuyensinh247.com, Cam kết giúp học sinh học tốt, bứt phá điểm 9,10 chỉ sau 3 tháng, hoàn trả học phí nếu học không hiệu quả.
 |
 |
 |
 |
 |
 |
 |
 |
