 Đề thi toán 10, đề kiểm tra toán 10 cánh diều có đáp án và lời giải chi tiết
Đề thi toán 10, đề kiểm tra toán 10 cánh diều có đáp án và lời giải chi tiết
 Đề thi học kì 1 Toán 10 - Cánh diều
Đề thi học kì 1 Toán 10 - Cánh diều Đề cương ôn tập học kì 1 Toán 10 - Cánh diều
Tải vềA. Nội dung ôn tập Mệnh đề và tập hợp 1. Mệnh đề toán học 2. Tập hợp. Các phép toán trên tập hợp Bất phương trình và hệ bất phương trình bậc nhất hai ẩn 1. Bất phương trình bậc nhất hai ẩn 2. Hệ bất phương trình bậc nhất hai ẩn
A. NỘI DUNG ÔN TẬP
Mệnh đề và tập hợp
1. Mệnh đề toán học
2. Tập hợp. Các phép toán trên tập hợp
Bất phương trình và hệ bất phương trình bậc nhất hai ẩn
1. Bất phương trình bậc nhất hai ẩn
2. Hệ bất phương trình bậc nhất hai ẩn
Hàm số bậc hai và đồ thị
1. Hàm số và đồ thị
2. Hàm số bậc hai. Đồ thị hàm số bậc hai và ứng dụng
3. Dấu của tam thức bậc hai
4. Bất phương trình bậc hai một ẩn
5. Hai dạng bất phương trình quy về phương trình bậc hai
Hệ thức lượng trong tam giác. Vecto
1. Giá trị lượng giác của một góc từ \({0^o}\) đến \({180^o}\). Định lí cosin và định lí sin trong tam giác
2. Giải tam giác
3. Khái niệm vecto
4. Tổng và hiệu của hai vectơ
5. Tích của một số với một vecto
6. Tích vô hướng của hai vectơ
B. BÀI TẬP
ĐỀ BÀI
Phần I: Trắc nghiệm nhiều phương án lựa chọn
Câu 1. Các kí hiệu nào sau đây dùng để viết đúng mệnh đề “7 là một số tự nhiên”?
A. \(7 \subset \mathbb{N}\)
B. \(7 \in \mathbb{N}\)
C. \(7 < \mathbb{N}\)
D. \(7 \le \mathbb{N}\)
Câu 2. Trong các tập hợp sau, tập hợp nào là tập hợp rỗng?
A. \(A = \{ x \in \mathbb{Z}|\left| x \right| < 1\} \)
B. \(B = \{ x \in \mathbb{Z}|6{x^2} - 7x + 1 = 0\} \)
C. \(C = \{ x \in \mathbb{Z}|{x^2} - 4x + 2 = 0\} \)
D. \(C = \{ x \in \mathbb{R}|{x^2} - 4x + 3 = 0\} \)
Câu 3. Cặp số nào dưới đây là nghiệm của bất phương trình 2x – y > 3?
A. (3;1)
B. (-1;4)
C. (2;-3)
D. (1;-2)
Câu 4. Miền tam giác ABC kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
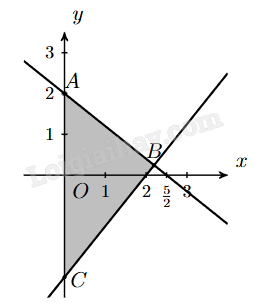
A. \(\left\{ \begin{array}{l}y \ge 0\\5x - 4y \ge 10\\5x + 4y \le 10\end{array} \right.\)
B. \(\left\{ \begin{array}{l}x > 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\)
C. \(\left\{ \begin{array}{l}x \ge 0\\4x - 5y \le 10\\5x + 4y \le 10\end{array} \right.\)
D. \(\left\{ \begin{array}{l}x \ge 0\\5x - 4y \le 10\\4x + 5y \le 10\end{array} \right.\)
Câu 5. Tam giác ABC vuông ở A có \(\widehat B = {30^o}\). Khẳng định nào sau đây là sai?
A. \(\cos B = \frac{1}{{\sqrt 3 }}\)
B. \(\sin C = \frac{{\sqrt 3 }}{2}\)
C. \(\cos C = \frac{1}{2}\)
D. \(\sin B = \frac{1}{2}\)
Câu 6. Tam giác có độ dài ba cạnh lần lượt là 9, 10, 11 có diện tích bằng
A. \(15\sqrt 2 \)
B. \(30\sqrt 2 \)
C. \(50\sqrt 3 \)
D. \(25\sqrt 3 \)
Câu 7. Tìm tập xác định của hàm số \(y = \frac{{x - 2}}{{x - 1}}\)?
A. \(D = \mathbb{R}\backslash \{ 1\} \)
B. \(D = \mathbb{R}\backslash \{ 1;2\} \)
C. \(D = \mathbb{R}\)
D. \(D = \mathbb{R}\backslash \{ 2\} \)
Câu 8. Cho hình bình hành tâm O. Khi đó \(\overrightarrow {OA} + \overrightarrow {BO} \) bằng
A. \(\overrightarrow {OC} + \overrightarrow {OB} \)
B. \(\overrightarrow {AB} \)
C. \(\overrightarrow {CD} \)
D. \(\overrightarrow {OC} + \overrightarrow {DO} \)
Câu 9. Gọi G là trọng tâm tam giác vuông ABC với cạnh huyền BC = 45. Tính \(\left| {\overrightarrow {GB} + \overrightarrow {GC} } \right|\)?
A. 45
B. \(3\sqrt 5 \)
C. 15
D. 30
Câu 10. Cho parabol (P): \(y = 3{x^2} - 2x + 1\). Điểm nào sau đây là đỉnh của (P)?
A. \(I\left( {\frac{1}{3};\frac{2}{3}} \right)\)
B. \(I\left( {0;1} \right)\)
C. \(I\left( { - \frac{1}{3};\frac{2}{3}} \right)\)
D. \(I\left( {\frac{1}{3}; - \frac{2}{3}} \right)\)
Câu 11. Cho hàm số \(y = {x^2} - 2x - 3\). Khẳng định nào sau đây là đúng?
A. Đồ thị hàm số là một đường thẳng
B. Đồ thị hàm số là một parabol
C. Hàm số đồng biến trên \(\mathbb{R}\)
D. Hàm số nghịch biến trên \(\mathbb{R}\)
Câu 12. Với số thực a bất kì, biểu thức nào sau đây luôn nhận giá trị dương?
A. \({a^2} + 2a - 1\)
B. \({a^2} - 2a + 1\)
C. \({a^2} + a + 1\)
D. \({a^2} + 2a + 1\)
Phần II: Trắc nghiệm đúng sai
Câu 13. Cho đồ thị hàm số bậc hai y = f(x) có dạng như hình sau:
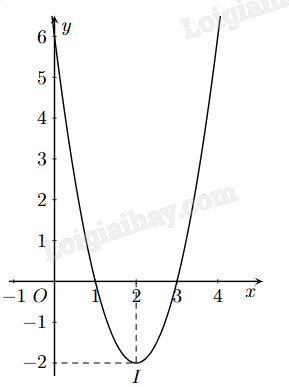
a) Trục đối xứng của đồ thị là đường thẳng x = -2.
b) Đỉnh I của đồ thị hàm số có tọa độ là (2;-2).
c) Đồ thị hàm số đi qua điểm A(0;6).
d) Hàm số đã cho là \(y = 2{x^2} - 2x + 6\).
Câu 14. Cho tam giác ABC biết a = BC = 3 cm, b = AC = 4 cm, \(\widehat C = {30^o}\). Khi đó
a) \(\cos \widehat C = \frac{{\sqrt 3 }}{2}\).
b) \(\cos (\widehat A + \widehat B) = \frac{{\sqrt 3 }}{2}\).
c) \(c \approx 3,05\) cm.
d) \(\cos A \approx 0,68\).
Câu 15. Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Đặt \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {AC} = \overrightarrow b \).
a) \(\overrightarrow {AI} = \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
b) \(\overrightarrow {IG} = - \frac{1}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b \).
c) \(\overrightarrow {BI} = - \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
d) \(\overrightarrow {CI} = \frac{1}{2}\overrightarrow a - \frac{1}{2}\overrightarrow b \).
Câu 16. Cho \(f(x) = ( - {x^2} + 3x)(2{x^2} + 1)\).
a) \(f(x) = 0 \Leftrightarrow \) x = 0 hoặc x = 3.
b) \(2{x^2} + 1 > 0\), \(\forall x \in \mathbb{R}\).
c) \(f(x) > 0\), \(\forall x \in ( - \infty ;0) \cup (3; + \infty )\).
d) \(f(x) < 0\), \(\forall x \in (0;3)\).
Phần III: Trắc nghiệm trả lời ngắn
Câu 17. Cho hàm số \(y = 2{x^2} - 5x + 2\) có đồ thị là parabol (P). Tính tổng tất cả các hoành độ giao điểm của đồ thị với trục tung và trục hoành (viết kết quả dưới dạng số thập phân).
Câu 18. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 100 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 5 triệu đồng, có thể chiết xuất được 20 kg chất A. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 1,5 kg chất B. Biết mỗi kg chất A có giá 0,5 triệu đồng, mỗi kg chất B có giá 5 triệu đồng. Hỏi phải dùng bao nhiêu tấn nguyên liệu loại I để lợi nhuận thu về là lớn nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 8 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Câu 19. Khoảng cách từ B đến cọc tiêu C không thể đo trực tiếp vì phải qua một đầm lầy. Người ta xác định một điêm A có khoảng cách AB = 5 m và đo được \(\widehat {BAC} = {60^o}\) (xem hình vẽ). Tính khoảng cách BC biết rằng AC = 8 m.
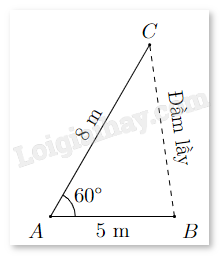
Câu 20. Cho tam giác ABC có đường trung tuyến AM. Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} = A{M^2} - kB{C^2}\). Khi đó, k bằng bao nhiêu (viết kết quả dưới dạng số thập phân).
Câu 21. Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm thì số lượng cá trong hồ tăng thêm x lần so với lượng cá ban đầu và x không đổi. Bằng cách thay đổi kỹ thuật nuôi và thức ăn cho cá. Hỏi sau hai năm đề số cá trong hồ là 36000 con thì tốc độ tăng số lượng cá trong hồ x là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.
Câu 22. Biết tập xác định của hàm số \(y = \frac{{x + 2}}{{\sqrt {x - 2\sqrt {x - 1} } }}\) có dạng \(D = [a; + \infty )\backslash \{ b\} \). Tính a + b.
ĐÁP ÁN
Phần I: Trắc nghiệm nhiều phương án lựa chọn

Phần II: Trắc nghiệm đúng sai
Câu 13. Cho đồ thị hàm số bậc hai y = f(x) có dạng như hình sau:
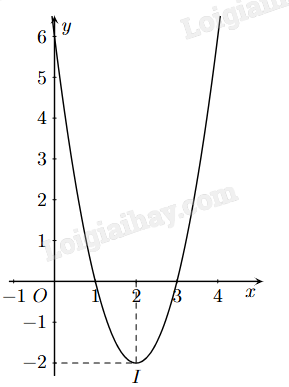
a) Trục đối xứng của đồ thị là đường thẳng x = -2.
b) Đỉnh I của đồ thị hàm số có tọa độ là (2;-2).
c) Đồ thị hàm số đi qua điểm A(0;6).
d) Hàm số đã cho là \(y = 2{x^2} - 2x + 6\).
Phương pháp giải:
Quan sát đồ thị và trả lời.
Lời giải chi tiết:
a) Sai. Trục đối xứng của đồ thị là đường thẳng x = 2.
b) Đúng. Đỉnh I của đồ thị hàm số có tọa độ là (2;-2).
c) Đúng. Đồ thị hàm số đi qua điểm A(0;6).
d) Sai. Đồ thị hàm số là đường parabol nên hàm số có dạng \(y = a{x^2} + bx + c\) \((a \ne 0)\).
Đỉnh của đồ thị có tọa độ (2;-2) suy ra \(\frac{{ - b}}{{2a}} = 2 \Leftrightarrow 4a + b = 0\).
Đồ thị đi qua điểm có tọa độ (0;6) và (1;0) suy ra \(\left\{ \begin{array}{l}6 = a{.0^2} + b.0 + c\\0 = a{.1^2} + b.1 + c\end{array} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}c = 6\\a + b + c = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}c = 6\\a + b = - 6\end{array} \right.\)
Từ đó ta có hệ \(\left\{ \begin{array}{l}4a + b = 0\\a + b = - 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = - 8\end{array} \right.\)
Vậy hàm số của đồ thị trên là \(y = 2{x^2} - 8x + 6\).
Câu 14. Cho tam giác ABC biết a = BC = 3 cm, b = AC = 4 cm, \(\widehat C = {30^o}\). Khi đó
a) \(\cos \widehat C = \frac{{\sqrt 3 }}{2}\).
b) \(\cos (\widehat A + \widehat B) = \frac{{\sqrt 3 }}{2}\).
c) \(c \approx 3,05\) cm.
d) \(\cos A \approx 0,68\).
Phương pháp giải:
a) Dựa vào giá trị lượng giác của một góc.
b) Sử dụng công thức \(\cos ({180^o} - \alpha ) = - \cos \alpha \).
c) Sử dụng định lý Cosin trong tam giác.
d) Sử dụng định lý Cosin trong tam giác.
Lời giải chi tiết:
a) Đúng. Ta có \(\cos {30^o} = \frac{{\sqrt 3 }}{2}\).
b) Sai. Ta có \(\widehat C = {180^o} - (\widehat A + \widehat B)\) nên \(\cos (\widehat A + \widehat B) = - \cos \widehat C = - \frac{{\sqrt 3 }}{2}\).
c) Sai. Ta có \({c^2} = {b^2} + {a^2} - 2ba\cos C = {4^2} + {3^2} - 2.4.3.\frac{{\sqrt 3 }}{2} = 25 - 12\sqrt 3 \) suy ra \(c \approx 2,05\).
d) Đúng. Ta có \(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{4^2} + 25 - 12\sqrt 3 - {3^2}}}{{2.4.\sqrt {25 - 12\sqrt 3 } }} \approx 0,68\).
Câu 15. Cho tam giác ABC có G là trọng tâm và I là trung điểm của đoạn thẳng BC. Đặt \(\overrightarrow {AB} = \overrightarrow a \), \(\overrightarrow {AC} = \overrightarrow b \).
a) \(\overrightarrow {AI} = \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
b) \(\overrightarrow {IG} = - \frac{1}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b \).
c) \(\overrightarrow {BI} = - \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
d) \(\overrightarrow {CI} = \frac{1}{2}\overrightarrow a - \frac{1}{2}\overrightarrow b \).
Phương pháp giải:
Sử dụng quy tắc cộng, trừ, nhân vecto với một số, tính chất của trung điểm và trọng tâm.
Lời giải chi tiết:
a) Đúng. Vì I là trung điểm của BC nên \(\overrightarrow {AI} = \frac{1}{2}\overrightarrow {AB} + \frac{1}{2}\overrightarrow {AC} = \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
b) Sai. Có G là trọng tâm và AI là đường trung tuyến của tam giác ABC nên:
\(\overrightarrow {IG} = - \frac{1}{3}\overrightarrow {AI} = - \frac{1}{3}\left( {\frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b } \right) = - \frac{1}{6}\overrightarrow a - \frac{1}{6}\overrightarrow b \).
c) Đúng. \(\overrightarrow {BI} = \overrightarrow {AI} - \overrightarrow {AB} = \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b - \overrightarrow a = - \frac{1}{2}\overrightarrow a + \frac{1}{2}\overrightarrow b \).
d) Đúng. Vì IC = BI và \(\overrightarrow {CI} \), \(BI\) ngược hướng nên \(\overrightarrow {CI} = - \overrightarrow {BI} = \frac{1}{2}\overrightarrow a - \frac{1}{2}\overrightarrow b \).
Câu 16. Cho \(f(x) = ( - {x^2} + 3x)(2{x^2} + 1)\).
a) \(f(x) = 0 \Leftrightarrow \) x = 0 hoặc x = 3.
b) \(2{x^2} + 1 > 0\), \(\forall x \in \mathbb{R}\).
c) \(f(x) > 0\), \(\forall x \in ( - \infty ;0) \cup (3; + \infty )\).
d) \(f(x) < 0\), \(\forall x \in (0;3)\).
Phương pháp giải:
Giải phương trình và sử dụng quy tắc “trong trái ngoài cùng” để xét dấu.
Lời giải chi tiết:
a) Đúng. \(f(x) = 0\) khi \( - {x^2} + 3x = 0\) (1) hoặc \(2{x^2} + 1 = 0\) (2).
Giải phương trình (1) được x = 0 hoặc x = 3.
Giải phương trình (2) thấy vô nghiệm.
Vậy \(f(x) = 0 \Leftrightarrow \) x = 0 hoặc x = 3.
b) Đúng. \(2{x^2} + 1 > 0\), \(\forall x \in \mathbb{R}\) vì phương trình \(2{x^2} + 1 = 0\) vô nghiệm và a = 2 > 0.
c) Sai. Vì \(2{x^2} + 1 > 0\) \(\forall x \in \mathbb{R}\) nên dấu của f(x) là dấu của \( - {x^2} + 3x\).
Áp dụng quy tắc “trong trái ngoài cùng” ta được \( - {x^2} + 3x > 0\) \(\forall x \in (0;3)\).
Vậy \(f(x) > 0\) \(\forall x \in (0;3)\).
d) Sai. Áp dụng quy tắc “trong trái ngoài cùng” ta được \( - {x^2} + 3x < 0\) \(\forall x \in ( - \infty ;0) \cup (3; + \infty )\).
Vậy \(f(x) < 0\) \(\forall x \in ( - \infty ;0) \cup (3; + \infty )\).
Phần III: Trắc nghiệm trả lời ngắn
Câu 17. Cho hàm số \(y = 2{x^2} - 5x + 2\) có đồ thị là parabol (P). Tính tổng tất cả các hoành độ giao điểm của đồ thị với trục tung và trục hoành (viết kết quả dưới dạng số thập phân).
Phương pháp giải:
Lập phương trình hoành độ giao điểm của đồ thị với hai trục, tìm nghiệm rồi tính tổng các nghiệm.
Lời giải chi tiết:
Phương trình hoành độ giao điểm của đồ thị (P) với trục hoành: \(2{x^2} - 5x + 2 = 0\).
Giải phương trình trên ta được hai nghiệm x = 2 và x = \(\frac{1}{2}\).
Đồ thị (P) cắt trục tung tại điểm có hoành độ x = 0.
Vậy tổng tất cả các hoành độ giao điểm của đồ thị (P) với trục tung và trục hoành là:
\(0 + 2 + \frac{1}{2} = \frac{5}{2} = 2,5\).
Đáp án: 2,5.
Câu 18. Người ta dự định dùng hai loại nguyên liệu để chiết xuất ít nhất 100 kg chất A và 9 kg chất B. Từ mỗi tấn nguyên liệu loại I giá 5 triệu đồng, có thể chiết xuất được 20 kg chất A. Từ mỗi tấn nguyên liệu loại II giá 3 triệu đồng có thể chiết xuất được 1,5 kg chất B. Biết mỗi kg chất A có giá 0,5 triệu đồng, mỗi kg chất B có giá 5 triệu đồng. Hỏi phải dùng bao nhiêu tấn nguyên liệu loại I để lợi nhuận thu về là lớn nhất, biết rằng cơ sở cung cấp nguyên liệu chỉ có thể cung cấp không quá 8 tấn nguyên liệu loại I và không quá 9 tấn nguyên liệu loại II.
Phương pháp giải:
Lập hệ bất phương trình.
Lời giải chi tiết:
Gọi x, y \((0 \le x \le 8,0 \le y \le 9)\) lần lượt là số tấn nguyên liệu loại I và loại II cần dùng.
Từ x tấn nguyên liệu loại I chiết xuất được 20x kg chất A.
Từ y tấn nguyên liệu loại II chiết xuất được 1,5 kg chất B.
Ta có hệ bất phương trình \(\left\{ \begin{array}{l}20x \ge 100\\1,5y \ge 9\\0 \le x \le 8\\0 \le y \le 9\end{array} \right.\) hay \(\left\{ \begin{array}{l}x \ge 5\\y \ge 6\\0 \le x \le 8\\0 \le y \le 9\end{array} \right.\)
Lợi nhuận thu về là \(F(x;y) = 0,5.20x + 5.1,5y - 5x - 3y = 5x + 4,5y\).
Miền nghiệm biểu diễn là miền tứ giác ABCD có A(5;6), B(8;6), C(8;9), D(5;9).
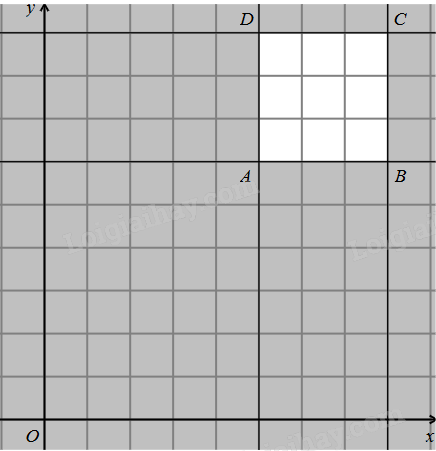
Tính giá trị của F(x;y) tại các đỉnh A, B, C, D tìm được giá trị lớn nhất là F(8;9) = 80,5.
Vậy cần sử dựng 8 tấn nguyên liệu loại I và 9 tấn nguyên liệu loại II.
Đáp án: 8.
Câu 19. Khoảng cách từ B đến cọc tiêu C không thể đo trực tiếp vì phải qua một đầm lầy. Người ta xác định một điêm A có khoảng cách AB = 5 m và đo được \(\widehat {BAC} = {60^o}\) (xem hình vẽ). Tính khoảng cách BC biết rằng AC = 8 m.
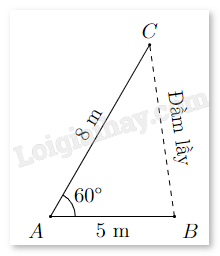
Phương pháp giải:
Sử dụng định lí Cosin trong tam giác.
Lời giải chi tiết:
Áp dụng định lí Cosin trong tam giác ABC có:
\(B{C^2} = A{C^2} + A{B^2} - 2AC.AB\cos A\)
\(B{C^2} = {8^2} + {5^2} - 2.5.8\cos {60^o} = 49\).
Vậy BC = 7 m.
Đáp án: 7.
Câu 20. Cho tam giác ABC có đường trung tuyến AM. Khi đó \(\overrightarrow {AB} .\overrightarrow {AC} = A{M^2} - kB{C^2}\). Khi đó, k bằng bao nhiêu (viết kết quả dưới dạng số thập phân).
Phương pháp giải:
Sử dụng công thức \(a.b = {(a + b)^2} - {(a - b)^2}\).
Tính chất trung điểm: Nếu I là trung điểm của AB thì \(\overrightarrow {MA} + \overrightarrow {MB} = 2\overrightarrow {MI} \).
Lời giải chi tiết:
\(\overrightarrow {AB} .\overrightarrow {AC} = \frac{{{{\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right)}^2} - {{\left( {\overrightarrow {AB} - \overrightarrow {AC} } \right)}^2}}}{4} = \frac{{4A{M^2} - B{C^2}}}{4} = A{M^2} - \frac{1}{4}B{C^2}\).
Vậy \(k = \frac{1}{4} = 0,25\).
Đáp án: 0,25.
Câu 21. Một người nông dân thả 1000 con cá giống vào hồ nuôi vừa mới đào. Biết rằng sau mỗi năm thì số lượng cá trong hồ tăng thêm x lần so với lượng cá ban đầu và x không đổi. Bằng cách thay đổi kỹ thuật nuôi và thức ăn cho cá. Hỏi sau hai năm đề số cá trong hồ là 36000 con thì tốc độ tăng số lượng cá trong hồ x là bao nhiêu? Biết tốc độ tăng mỗi năm là không đổi.
Phương pháp giải:
Lập phương trình bậc hai theo ẩn x mô tả số lượng cá rồi giải ra nghiệm.
Lời giải chi tiết:
Sau 1 năm, số lượng cá trong hồ là \(1000 + 1000x = 1000(1 + x)\) (con).
Sau 2 năm, số lượng cá trong hồ là \(1000(1 + x) + 1000(1 + x) = 1000{(1 + x)^2}\) (con).
Điều kiện: \(x > 0\).
Để số lượng cá trong hồ sau 2 năm là 36000 thì ta có \(1000{(1 + x)^2} = 36000 \Leftrightarrow \left[ \begin{array}{l}x = 5\\x = - 7\end{array} \right.\).
Loại x = -7.
Vậy tốc độ tăng số cá mỗi năm là x = 5.
Đáp án: 5.
Câu 22. Biết tập xác định của hàm số \(y = \frac{{x + 2}}{{\sqrt {x - 2\sqrt {x - 1} } }}\) có dạng \(D = [a; + \infty )\backslash \{ b\} \). Tính a + b.
Phương pháp giải:
Hàm số xác định khi biểu thức dưới dấu căn lớn hơn hoặc bằng 0, mẫu thức khác 0.
Lời giải chi tiết:
Hàm số xác định khi \(\left\{ \begin{array}{l}\sqrt {x - 2\sqrt {x - 1} } > 0\\x - 1 \ge 0\end{array} \right.\) \(\begin{array}{*{20}{c}}{(1)}\\{(2)}\end{array}\)
Giải (2): \(x - 1 \ge 0\) suy ra \(x \ge 1\).
Giải (1): \(\sqrt {x - 2\sqrt {x - 1} } = \sqrt {(x - 1) - 2\sqrt {x - 1} + 1} = \sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} > 0\).
Vì \({\left( {\sqrt {x - 1} - 1} \right)^2} \ge 0\) \(\forall x \ge 1\) nên \(\sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} \ge 0\) \(\forall x \ge 1\).
Do đó, để \(\sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} > 0\) thì \(\sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} \ne 0\) hay \({\left( {\sqrt {x - 1} - 1} \right)^2} \ne 0\).
Khi đó \(\sqrt {x - 1} \ne 1\) hay \(x \ne 2\).
Từ (1) và (2) ta được \(D = [1; + \infty )\backslash \{ 2\} \).
Ta có a = 1, b = 2. Vậy a + b = 3.
Đáp án: 3.












Danh sách bình luận