40 bài tập trắc nghiệm nguyên hàm mức độ vận dụng, vận dụng cao
Làm đề thiCâu hỏi 1 :
Một tay đua đang điều khiển chiếc xe đua của mình với vận tốc \(180km/h.\)Tay đua nhấn ga để về đích kể từ đó xe chạy với gia tốc \(a\left( t \right) = 2t + 1\,\left( {m/{s^2}} \right)\) . Hỏi rằng \(4s\) sau khi tay đua nhấn ga thì xe đua chạy với vận tốc bao nhiêu \(km/h.\)
- A \(200km/h\)
- B \(252km/h\)
- C \(288km/h\)
- D \(243km/h\)
Đáp án: A
Phương pháp giải:
\(v\left( t \right) = \int\limits_{}^{} {a\left( t \right)dt} \).
Lời giải chi tiết:
Ta có \(v\left( t \right) = \int\limits_{}^{} {a\left( t \right)dt} = \int\limits_{}^{} {\left( {2t + 1} \right)dt} = {t^2} + t + C\)
Do \(v\left( 0 \right) = 180 \Leftrightarrow C = 180 \Rightarrow v\left( t \right) = {t^2} + t + 180\).
\( \Rightarrow v\left( 4 \right) = {4^2} + 4 + 180 = 200\,\,\left( {m/s} \right)\).
Chọn A.
Câu hỏi 2 :
Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \frac{1}{{x\ln x}}\) thỏa mãn \(F\left( {\frac{1}{e}} \right) = 2\) và \(F\left( e \right) = \ln 2.\) Giá trị của biểu thức \(F\left( {\frac{1}{{{e^2}}}} \right) + F\left( {{e^2}} \right)\) bằng
- A \(3\ln 2 + 2.\)
- B \(\ln 2 + 2.\)
- C \(\ln 2 + 1.\)
- D \(2\ln 2 + 1.\)
Đáp án: A
Phương pháp giải:
- Tìm nguyên hàm bằng phương pháp đổi biến.
- Thay \(x = \frac{1}{e},\,\,\,x = e\) tìm hằng số \(C\) suy ra hàm số \(F\left( x \right)\).
- Thay các giá trị \(\frac{1}{{{e^2}}}\) và \({e^2}\) vào \(F\left( x \right)\) và tính.
Lời giải chi tiết:
Ta có: \(F\left( x \right) = \int {f\left( x \right)dx} = \int {\frac{{dx}}{{x\ln x}}} \).
Đặt \(\ln x = t \Rightarrow \frac{{dx}}{x} = dt\)
\( \Rightarrow \int {\frac{{dx}}{{x\ln x}}} = \int {\frac{{dt}}{t}} = \ln \left| t \right| + C = \ln \left| {\ln x} \right| + C = \left\{ \begin{array}{l}\ln \left( {\ln x} \right) + {C_1}\,\,khi\,\,x > 1\\\ln \left( { - \ln x} \right) + {C_2}\,\,khi\,\,x < 1\end{array} \right.\)
+) \(F\left( {\frac{1}{e}} \right) = 2 \Leftrightarrow \ln \left( { - \ln \frac{1}{e}} \right) + {C_1} = 2 \Leftrightarrow {C_1} = 2\).
+) \(F\left( e \right) = \ln 2 \Leftrightarrow \ln \left( {\ln e} \right) + {C_2} = \ln 2 \Leftrightarrow {C_2} = \ln 2\)
\( \Rightarrow F\left( x \right) = \left\{ \begin{array}{l}\ln \left( {\ln x} \right) + 2\,\,\,\,\,\,\,\,\,\,khi\,\,x > 1\\\ln \left( { - \ln x} \right) + \ln 2\,\,khi\,\,x < 1\end{array} \right.\)
\( \Rightarrow F\left( {\frac{1}{{{e^2}}}} \right) = \ln \left( { - \ln \frac{1}{{{e^2}}}} \right) + \ln 2 = 2\ln 2\) và \(F\left( {{e^2}} \right) = \ln \left( {\ln {e^2}} \right) + 2 = \ln 2 + 2\)
\( \Rightarrow F\left( {\frac{1}{{{e^2}}}} \right) + F\left( {{e^2}} \right) = 2\ln 2 + \ln 2 + 2 = 3\ln 2 + 2\).
Chọn A.
Câu hỏi 3 :
Cho hàm số \(y = f\left( x \right)\) thoả mãn \(f\left( 2 \right) = - \frac{4}{{19}}\) và \(f'\left( x \right) = {x^3}{f^2}\left( x \right)\,\,\forall x \in \mathbb{R}.\) Giá trị của \(f\left( 1 \right)\) bằng
- A \( - \frac{2}{3}.\)
- B \( - \frac{1}{2}.\)
- C \( - 1.\)
- D \( - \frac{3}{4}.\)
Đáp án: C
Phương pháp giải:
Biến đổi giả thiết rồi lấy nguyên hàm hai vế.
Chú ý \(d\left( {f\left( x \right)} \right) = f'\left( x \right)dx\) hoặc đặt ẩn phụ \(f\left( x \right) = t\) .
Lời giải chi tiết:
Ta có \(f'\left( x \right) = {x^3}{f^2}\left( x \right)\,\, \Leftrightarrow \frac{{f'\left( x \right)}}{{{f^2}\left( x \right)}} = {x^3}\)
Lấy nguyên hàm hai vế ta được \(\int {\frac{{f'\left( x \right)}}{{{f^2}\left( x \right)}}dx} = \int {{x^3}dx} \Leftrightarrow \int {\frac{1}{{{f^2}\left( x \right)}}d\left( {f\left( x \right)} \right)} = \frac{{{x^4}}}{4} + C\)
\( \Leftrightarrow - \frac{1}{{f\left( x \right)}} = \frac{{{x^4}}}{4} + C \Rightarrow f\left( x \right) = \frac{{ - 1}}{{\frac{{{x^4}}}{4} + C}}\)
Mà \(f\left( 2 \right) = - \frac{4}{{19}}\) nên \(f\left( 2 \right) = \frac{{ - 1}}{{\frac{{{2^4}}}{4} + C}} \Leftrightarrow \frac{{19}}{4} = 4 + C \Leftrightarrow C = \frac{3}{4} \Leftrightarrow f\left( x \right) = \frac{{ - 4}}{{{x^4} + 3}}\)
Suy ra \(f\left( 1 \right) = \frac{{ - 4}}{{{1^4} + 3}} = - 1.\)
Chọn C.
Câu hỏi 4 :
Cho \(F\left( x \right) = {x^2}\) là một nguyên hàm của hàm số \(f\left( x \right).{e^{2x}}\). Tìm nguyên hàm của hàm số \(f'\left( x \right).{e^{2x}}\).
- A \(\int {f'\left( x \right).{e^{2x}}} dx = - 2{x^2} + 2x + C\)
- B \(\int {f'\left( x \right).{e^{2x}}} dx = - {x^2} + x + C\).
- C \(\int {f'\left( x \right).{e^{2x}}} dx = - {x^2} + 2x + C\).
- D \(\int {f'\left( x \right).{e^{2x}}} dx = 2{x^2} - 2x + C\).
Đáp án: A
Phương pháp giải:
Áp dụng công thức từng phần \(\int\limits_{}^{} {udv} = uv - \int\limits_{}^{} {vdu} \).
Lời giải chi tiết:
\(F\left( x \right) = {x^2}\) là một nguyên hàm của hàm số \(f\left( x \right).{e^{2x}} \Rightarrow {\left( {{x^2}} \right)^\prime } = f\left( x \right).{e^{2x}} \Leftrightarrow 2x = f\left( x \right).{e^{2x}}\)
Ta có:
\(\begin{array}{l}\int {f'\left( x \right).{e^{2x}}} dx = \int {{e^{2x}}} d\left( {f\left( x \right)} \right) = {e^{2x}}f\left( x \right) - \int {f\left( x \right)d\left( {{e^{2x}}} \right)} \\ = {e^{2x}}f\left( x \right) - 2\int {f\left( x \right){e^{2x}}} dx = 2x - 2{x^2} + C\end{array}\)
Chọn: A
Câu hỏi 5 :
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ { - 1;1} \right\}\) thỏa mãn \(f'\left( x \right) = \dfrac{1}{{{x^2} - 1}}\). Biết \(f\left( 3 \right) + f\left( { - 3} \right) = 4\) và \(f\left( {\dfrac{1}{3}} \right) + f\left( { - \dfrac{1}{3}} \right) = 2\). Giá trị của biểu thức \(f\left( { - 5} \right) + f\left( 0 \right) + f\left( 2 \right)\) bằng:
- A \(5 - \dfrac{1}{2}\ln 2\)
- B \(6 - \dfrac{1}{2}\ln 2\)
- C \(5 + \dfrac{1}{2}\ln 2\)
- D \(6 + \dfrac{1}{2}\ln 2\)
Đáp án: A
Phương pháp giải:
Sử dụng công thức giải nhanh: \(\int\limits_{}^{} {\dfrac{{dx}}{{\left( {x - a} \right)\left( {x - b} \right)}}} = \dfrac{1}{{a - b}}\ln \left| {\dfrac{{x - a}}{{x - b}}} \right| + C\).
Lời giải chi tiết:
\(\begin{array}{l}f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx} = \int\limits_{}^{} {\dfrac{{dx}}{{{x^2} - 1}}} = \int\limits_{}^{} {\dfrac{{dx}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}} = \dfrac{1}{2}\ln \left| {\dfrac{{x - 1}}{{x + 1}}} \right| + C\\\,\,\,\,\,\,\,\,\,\,\,\, = \left[ \begin{array}{l}\dfrac{1}{2}\ln \dfrac{{x - 1}}{{x + 1}} + {C_1}\,\,khi\,\,x \ge 1\,\, \vee \,\,x \le - 1\\\dfrac{1}{2}\ln \dfrac{{1 - x}}{{x + 1}} + {C_2}\,\,khi\,\, - 1 \le x \le 1\end{array} \right.\\\left\{ \begin{array}{l}f\left( 3 \right) + f\left( { - 3} \right) = 4\\f\left( {\dfrac{1}{3}} \right) + f\left( { - \dfrac{1}{3}} \right) = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\dfrac{1}{2}\ln \dfrac{1}{2} + {C_1} + \dfrac{1}{2}\ln 2 + {C_1} = 4\\\dfrac{1}{2}\ln \dfrac{1}{2} + {C_2} + \dfrac{1}{2}\ln 2 + {C_2} = 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{C_1} = 2\\{C_2} = 1\end{array} \right.\\ \Rightarrow f\left( x \right) = \left[ \begin{array}{l}\dfrac{1}{2}\ln \dfrac{{x - 1}}{{x + 1}} + 2\,\,khi\,\,x \ge 1\,\, \vee \,\,x \le - 1\\\dfrac{1}{2}\ln \dfrac{{1 - x}}{{x + 1}} + 1\,\,khi\,\, - 1 \le x \le 1\end{array} \right.\\ \Rightarrow f\left( { - 5} \right) + f\left( 0 \right) + f\left( 2 \right) = \dfrac{1}{2}\ln \dfrac{3}{2} + 2 + \dfrac{1}{2}\ln 1 + 1 + \dfrac{1}{2}\ln \dfrac{1}{3} + 2\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{1}{2}\ln \dfrac{1}{2} + 5 = 5 - \dfrac{1}{2}\ln 2\end{array}\)
Chọn A.
Câu hỏi 6 :
Biết rằng \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) trên khoảng \(\left( { - \infty ; + \infty } \right)\). Gọi \(F\left( x \right)\) là một nguyên hàm của \(f'\left( x \right){e^x}\) thỏa mãn \(F\left( 0 \right) = 1\), giá trị của \(F\left( { - 1} \right)\) bằng:
- A \(\dfrac{7}{2}\)
- B \(\dfrac{{5 - e}}{2}\)
- C \(\dfrac{{7 - e}}{2}\)
- D \(\dfrac{5}{2}\)
Đáp án: A
Phương pháp giải:
+) \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) nên \(\left( {x{e^x}} \right)' = f\left( { - x} \right)\).
+) Từ \(f\left( { - x} \right) \Rightarrow f\left( x \right)\).
+) \(F\left( x \right)\) là một nguyên hàm của \(f'\left( x \right){e^x} \Rightarrow F\left( x \right) = \int\limits_{}^{} {f'\left( x \right){e^x}dx} \).
+) Tính \(F\left( x \right),\) từ đó tính \(F\left( { - 1} \right)\)
Lời giải chi tiết:
Vì \(x{e^x}\) là một nguyên hàm của hàm số \(f\left( { - x} \right)\) nên \(\left( {x{e^x}} \right)' = f\left( { - x} \right) \Leftrightarrow f\left( { - x} \right) = {e^x} + x{e^x} = {e^x}\left( {1 + x} \right)\).
\( \Rightarrow f\left( x \right) = {e^{ - x}}\left( {1 - x} \right)\).
\(\begin{array}{l} \Rightarrow f'\left( x \right) = - {e^{ - x}}\left( {1 - x} \right) - {e^{ - x}} = - {e^{ - x}}\left( {2 - x} \right) = \left( {x - 2} \right){e^{ - x}}\\ \Rightarrow f'\left( x \right){e^x} = \left( {x - 2} \right){e^{ - x}}.{e^x} = x - 2\\ \Rightarrow F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {\left( {x - 2} \right)dx} = \dfrac{{{x^2}}}{2} - 2x + C\\F\left( 0 \right) = 1 \Rightarrow C = 1 \Rightarrow F\left( x \right) = \dfrac{{{x^2}}}{2} - 2x + 1\\ \Rightarrow F\left( { - 1} \right) = \dfrac{{{{\left( { - 1} \right)}^2}}}{2} - 2\left( { - 1} \right) + 1 = \dfrac{7}{2}\end{array}\)
Chọn A.
Câu hỏi 7 :
Tìm nguyên hàm của hàm số \(y = x.{e^x}\)?
- A \(\int {x.{e^x}dx} = x.{e^x} + C\)
- B \(\int {x.{e^x}dx} = x.{e^x} - {e^x} + C\)
- C \(\int {x.{e^x}dx} = {e^x} + C\)
- D
\(\int {x.{e^x}dx} = x.{e^x} + {e^x} + C\)
Đáp án: B
Phương pháp giải:
Sử dụng phương pháp nguyên hàm từng phần: đặt \(\left\{ \begin{array}{l}u = x\\dv = {e^x}dx\end{array} \right.\).
Lời giải chi tiết:
Đặt \(\left\{ \begin{array}{l}u = x\\dv = {e^x}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = {e^x}\end{array} \right.\) .
\( \Rightarrow \int {x{e^x}dx} = x{e^x} - \int {{e^x}dx} = x{e^x} - {e^x} + C\).
Chọn B
Câu hỏi 8 :
Một bác thợ xây bơm nước vào bể chứa nước. Gọi \(V\left( t \right)\) là thể tích nước bơm được sau \(t\) giây. Biết rằng \(V'\left( t \right) = a{t^2} + bt\) và ban đầu bể không có nước, sau \(5\) giây thể tích nước trong bể là \(15\) \({m^3}\), sau \(10\) giây thì thể tích nước trong bể là \(110\) \({m^3}\). Thể tích nước trong bể sau khi bơm được \(20\) giây bằng
- A
\(60\) \({m^3}\)
- B
\(220\) \({m^3}\)
- C
\(840\) \({m^3}\)
- D
\(420\) \({m^3}\)
Đáp án:
Phương pháp giải:
Ứng dụng nguyên hàm để tìm hàm \(V(t)\): \(V\left( t \right) = \int\limits_{}^{} {V'\left( t \right)} dt\). Khi đó, \(V(t)\) là hàm đa thức bậc ba với các hệ số \(a\), \(b\), \(c\).
Dựa vào dữ kiện đề bài cho tại thời điểm \(t=0\), \(t=5\), \(t=10\), lập hệ phương trình bậc ba để tìm \(a\), \(b\), \(c\).
Tính \(V(20)\).
Lời giải chi tiết:
Ta có: \(V\left( t \right) = \int {V'\left( t \right)dt} = \int {\left( {a{t^2} + bt} \right)dt} = \frac{{a{t^3}}}{3} + \frac{{b{t^2}}}{2} + C\).
Theo đề bài ta có: \(\left\{ \begin{array}{l}V\left( 0 \right) = 0\\V\left( 5 \right) = 15\\V\left( {10} \right) = 110\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C = 0\\\frac{{125a}}{3} + \frac{{25b}}{2} = 15\\\frac{{1000a}}{3} + \frac{{100b}}{2} = 110\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = \frac{3}{{10}}\\b = \frac{1}{5}\end{array} \right.\)
\( \Rightarrow V\left( t \right) = \dfrac{1}{{10}}{t^3} + \dfrac{1}{10}{t^2} \Rightarrow V\left( {20} \right) = 840\,{m^3}\).
Câu hỏi 9 :
Cho \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = \dfrac{1}{{x\ln x}}\) thỏa mãn \(F\left( {\dfrac{1}{e}} \right) = 2,\,\,F\left( e \right) = \ln 2\). Giá trị của biểu thức \(F\left( {\dfrac{1}{{{e^2}}}} \right) + F\left( {{e^2}} \right)\) bằng:
- A
\(2\ln 2 + 1\)
- B \(\ln 2 + 1\)
- C \(\ln 2 + 2\)
- D / \(3\ln 2 + 2\)
Đáp án: D
Phương pháp giải:
\(F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx} \).
Lời giải chi tiết:
\(\begin{array}{l}F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {\dfrac{{dx}}{{x\ln x}}} = \int\limits_{}^{} {\dfrac{{d\left( {\ln x} \right)}}{{\ln x}}} = \ln \left| {\ln x} \right| + C\\F\left( x \right) = \left[ \begin{array}{l}\ln \left( {\ln x} \right) + {C_1}\,\,khi\,\,x \ge 1\\\ln \left( { - \ln x} \right) + {C_2}\,\,khi\,\,0 < x < 1\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}F\left( {\dfrac{1}{e}} \right) = 2\\F\left( e \right) = \ln 2\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{C_2} = 2\\{C_1} = \ln 2\end{array} \right.\\ \Rightarrow F\left( x \right) = \left[ \begin{array}{l}\ln \left( {\ln x} \right) + \ln 2\,\,khi\,\,x \ge 1\\\ln \left( { - \ln x} \right) + 2\,\,khi\,\,0 < x < 1\end{array} \right.\\ \Rightarrow \left\{ \begin{array}{l}F\left( {\dfrac{1}{{{e^2}}}} \right) = \ln \left( { - \ln \dfrac{1}{{{e^2}}}} \right) + 2 = \ln 2 + 2\\F\left( {{e^2}} \right) = \ln \left( {\ln {e^2}} \right) + \ln 2 = 2\ln 2\end{array} \right.\\ \Rightarrow F\left( {\dfrac{1}{{{e^2}}}} \right) + F\left( {{e^2}} \right) = 3\ln 2 + 2\end{array}\)
Chọn D.
Câu hỏi 10 :
Cho hàm số \(f\left( x \right)\) có đạo hàm trên \(\mathbb{R}\) thỏa mãn \(f'\left( x \right) - 2018f\left( x \right) = 2018.{x^{2017}}.{e^{2018x}}\) với mọi \(x \in \mathbb{R}\); \(f\left( 0 \right) = 2018\). Giá trị của \(f\left( 1 \right)\) là
- A \(f\left( 1 \right) = 2018{e^{ - 2018}}\)
- B \(f\left( 1 \right) = 2019{e^{ - 2018}}\)
- C \(f\left( 1 \right) = 2018{e^{2018}}\)
- D \(f\left( 1 \right) = 2019{e^{2018}}\)
Đáp án: D
Phương pháp giải:
- Nhân cả hai vế với \({e^{ - 2018x}}\) và lấy nguyên hàm hai vế.
- Sử dụng điều kiện \(f\left( 0 \right) = 2018\) tìm hàm \(f\left( x \right)\) và kết luận.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}f'\left( x \right) - 2018f\left( x \right) = 2018{x^{2017}}{e^{2018x}} \Leftrightarrow f'\left( x \right){e^{ - 2018x}} - 2018{e^{ - 2018x}}f\left( x \right) = 2018{x^{2017}}\\ \Rightarrow \left[ {f\left( x \right){e^{ - 2018x}}} \right]' = \left( {{x^{2018}}} \right)' \Rightarrow \int {\left[ {f\left( x \right){e^{ - 2018x}}} \right]'dx} = \int {\left( {{x^{2018}}} \right)'dx} \Rightarrow f\left( x \right){e^{ - 2018x}} = {x^{2018}} + C\end{array}\)
Do \(f\left( 0 \right) = 2018 \Rightarrow f\left( 0 \right).{e^0} = C \Leftrightarrow C = 2018\)
\(\begin{array}{l} \Rightarrow f\left( x \right) = {x^{2018}}{e^{2018x}} + 2018{e^{2018x}}\\ \Rightarrow f\left( 1 \right) = {e^{2018}} + 2018{e^{2018}} = 2019{e^{2018}}.\end{array}\)
Chọn D.
Câu hỏi 11 :
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f\left( 1 \right) = 3\) và \(x\left( {4 - f'\left( x \right)} \right) = f\left( x \right) - 1\) với mọi \(x > 0.\) Tính \(f\left( 2 \right).\)
- A \(5\)
- B \(3\)
- C \(6\)
- D \(2\)
Đáp án: A
Phương pháp giải:
Biến đổi giả thiết rồi lấy nguyên hàm hai vế để tìm được \(f\left( x \right).\) Lưu ý rằng \(\int {f'\left( x \right)dx} = f\left( x \right) + C\)
Từ đó tính \(f\left( 2 \right).\)
Lời giải chi tiết:
Ta có
\(\begin{array}{l}\,\,\,\,\,\,x\left( {4 - f'\left( x \right)} \right) = f\left( x \right) - 1 \Leftrightarrow 4x - xf'\left( x \right) = f\left( x \right) - 1\\ \Leftrightarrow f\left( x \right) + xf'\left( x \right) = 4x + 1 \Leftrightarrow {\left( {xf\left( x \right)} \right)^\prime } = 4x + 1\end{array}\)
Lấy nguyên hàm hai vế theo \(x\) ta được \(xf\left( x \right) = 2{x^2} + x + C\)
Mà \(f\left( 1 \right) = 3\) nên ta có \(1.f\left( 1 \right) = {2.1^2} + 1 + C \Leftrightarrow 3 = 3 + C \Rightarrow C = 0\)
Từ đó \(xf\left( x \right) = 2{x^2} + x \Rightarrow f\left( x \right) = 2x + 1\,\,\,\left( {do\,x > 0} \right)\)
Suy ra \(f\left( 2 \right) = 2.2 + 1 = 5.\)
Chọn A.
Câu hỏi 12 :
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(f\left( 0 \right) = 0,\,\,f'\left( x \right) = \dfrac{x}{{{x^2} + 1}}\). Họ nguyên hàm của hàm số \(g\left( x \right) = 4xf\left( x \right)\) là:
- A \(\left( {{x^2} + 1} \right)\ln \left( {{x^2}} \right) - {x^2} + c\)
- B \({x^2}\ln \left( {{x^2} + 1} \right) - {x^2}\)
- C \(\left( {{x^2} + 1} \right)\ln \left( {{x^2} + 1} \right) - {x^2} + c\)
- D \(\left( {{x^2} + 1} \right)\ln \left( {{x^2} + 1} \right) - {x^2}\)
Đáp án: C
Phương pháp giải:
+) \(f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx} \Rightarrow \) Xác định hàm số \(f\left( x \right)\).
+) Sử dụng phương pháp đổi biến và nguyên hàm từng phần tính nguyên hàm của hàm \(g\left( x \right)\).
Lời giải chi tiết:
\(\begin{array}{l}f'\left( x \right) = \dfrac{x}{{{x^2} + 1}}\\ \Rightarrow f\left( x \right) = \int\limits_{}^{} {f'\left( x \right)dx} = \int\limits_{}^{} {\dfrac{{xdx}}{{{x^2} + 1}}} = \dfrac{1}{2}\int\limits_{}^{} {\dfrac{{d\left( {{x^2} + 1} \right)}}{{{x^2} + 1}}} = \dfrac{1}{2}\ln \left( {{x^2} + 1} \right) + C\\f\left( 0 \right) = 0 \Leftrightarrow \dfrac{1}{2}\ln 1 + C = 0 \Leftrightarrow C = 0 \Rightarrow f\left( x \right) = \dfrac{1}{2}\ln \left( {{x^2} + 1} \right)\\ \Rightarrow g\left( x \right) = 4xf\left( x \right) = 2x\ln \left( {{x^2} + 1} \right) \Rightarrow \int\limits_{}^{} {g\left( x \right)dx} = \int\limits_{}^{} {2x\ln \left( {{x^2} + 1} \right)dx} \end{array}\)
Đặt \(t = {x^2} + 1 \Rightarrow dt = 2xdx\)
\(\begin{array}{l} \Rightarrow \int\limits_{}^{} {g\left( x \right)dx} = \int\limits_{}^{} {\ln tdt} = t\ln t - \int\limits_{}^{} {t.\dfrac{1}{t}dt} = t\ln t - \int\limits_{}^{} {dt} = t\ln t - t + C\\ = \left( {{x^2} + 1} \right)\ln \left( {{x^2} + 1} \right) - \left( {{x^2} + 1} \right) + C\end{array}\)
Đặt \( - 1 + C = c \Rightarrow \int\limits_{}^{} {g\left( x \right)dx} = \left( {{x^2} + 1} \right)\ln \left( {{x^2} + 1} \right) - {x^2} + c\).
Chọn C
Câu hỏi 13 :
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {0; + \infty } \right)\). Biết \(f'\left( x \right) = \dfrac{{\ln x}}{x}\) và \(f\left( 1 \right) = \dfrac{3}{2}\), tính \(f\left( 3 \right)\).
- A \(\dfrac{{\ln 3 - 3}}{2}\)
- B \(\dfrac{{{{\ln }^2}3 - 3}}{2}\)
- C \(\dfrac{{\ln 3 + 3}}{2}\)
- D \(\dfrac{{{{\ln }^2}3 + 3}}{2}\)
Đáp án: D
Phương pháp giải:
Sử dụng phương pháp đổi biến tìm nguyên hàm: Tìm hàm số \(f\left( x \right)\) và suy ra giá trị \(f\left( 3 \right)\).
Lời giải chi tiết:
Ta có : \(f\left( x \right) = \int {f'\left( x \right)dx} = \int {\dfrac{{\ln x}}{x}dx} \)
Đặt \(t = \ln x \Rightarrow dt = \dfrac{{dx}}{x}\) \( \Rightarrow \int {\dfrac{{\ln x}}{x}dx} = \int {tdt} = \dfrac{{{t^2}}}{2} + C = \dfrac{{{{\ln }^2}x}}{2} + C\)
\( \Rightarrow f\left( x \right) = \dfrac{{{{\ln }^2}x}}{2} + C\). Mà \(f\left( 1 \right) = \dfrac{3}{2} \Rightarrow C = \dfrac{3}{2} \Rightarrow f\left( x \right) = \dfrac{{{{\ln }^2}x}}{2} + \dfrac{3}{2}\)
Vậy \(f\left( 3 \right) = \dfrac{{{{\ln }^2}3}}{2} + \dfrac{3}{2} = \dfrac{{{{\ln }^2}3 + 3}}{2}\) .
Chọn D.
Câu hỏi 14 :
Biết \(\int {x.{{\left( {2x + 1} \right)}^{100}}dx} = \dfrac{{{{\left( {2x + 1} \right)}^{102}}}}{a} - \dfrac{{{{\left( {2x + 1} \right)}^{101}}}}{b} + C\), \(a,b \in \mathbb{Z}\). Giá trị của hiệu \(a - b\) bằng
- A 4
- B 2
- C 1
- D 0
Đáp án: A
Phương pháp giải:
Đặt ẩn phụ \(2x + 1 = t\).
Lời giải chi tiết:
Đặt \(2x + 1 = t \Leftrightarrow 2dx = dt\) và \(x = \dfrac{{t - 1}}{2}\), ta có:
\(\begin{array}{l}\int {x.{{\left( {2x + 1} \right)}^{100}}dx} = \int {\dfrac{1}{2}\left( {t - 1} \right){t^{100}}.\dfrac{1}{2}dt} = \dfrac{1}{4}\int {\left( {t - 1} \right){t^{100}}dt} = \dfrac{1}{4}\int {\left( {{t^{101}} - {t^{100}}} \right)dt} \\ = \dfrac{1}{4}\left( {\dfrac{{{t^{102}}}}{{102}} - \dfrac{{{t^{101}}}}{{101}}} \right) + C = \dfrac{{{{\left( {2x + 1} \right)}^{102}}}}{{408}} - \dfrac{{{{\left( {2x + 1} \right)}^{101}}}}{{404}} + C\\ \Rightarrow a = 408,\,\,b = 404 \Rightarrow a - b = 4.\end{array}\)
Chọn: A
Câu hỏi 15 :
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \dfrac{{2x + 1}}{{{{\left( {x + 2} \right)}^2}}}\) trên khoảng \(\left( { - 2; + \infty } \right)\) là
- A \(2\ln \left( {x + 2} \right) + \dfrac{1}{{x + 2}} + C\)
- B \(2\ln \left( {x + 2} \right) - \dfrac{1}{{x + 2}} + C\)
- C \(2\ln \left( {x + 2} \right) - \dfrac{3}{{x + 2}} + C\)
- D \(2\ln \left( {x + 2} \right) + \dfrac{3}{{x + 2}} + C\)
Đáp án: D
Phương pháp giải:
Đặt \(t = x + 2\), tính \(dx\) và thay vào tính nguyên hàm của hàm số đã cho.
Lời giải chi tiết:
Đặt \(t = x + 2\left( {t > 0} \right) \Rightarrow x = t - 2 \Rightarrow dx = dt\).
Khi đó
\(\begin{array}{l}\int {\dfrac{{2x + 1}}{{{{\left( {x + 2} \right)}^2}}}dx} = \int {\dfrac{{2\left( {t - 2} \right) + 1}}{{{t^2}}}dt} \\ = \int {\dfrac{{2t - 3}}{{{t^2}}}dt} = \int {\left( {\dfrac{2}{t} - \dfrac{3}{{{t^2}}}} \right)dt} \\ = 2\ln t + \dfrac{3}{t} + C = 2\ln \left( {x + 2} \right) + \dfrac{3}{{x + 2}} + C\end{array}\)
Chọn D.
Câu hỏi 16 :
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \dfrac{{3x - 2}}{{{{\left( {x - 2} \right)}^2}}}\) trên khoảng \(\left( {2; + \infty } \right)\) là:
- A \(3\ln \left( {x - 2} \right) + \dfrac{4}{{x - 2}} + C\).
- B \(3\ln \left( {x - 2} \right) + \dfrac{2}{{x - 2}} + C\).
- C \(3\ln \left( {x - 2} \right) - \dfrac{2}{{x - 2}} + C\).
- D \(3\ln \left( {x - 2} \right) - \dfrac{4}{{x - 2}} + C\).
Đáp án: D
Phương pháp giải:
Phân tích tử theo mẫu, sử dụng các công thức tính nguyên hàm cơ bản \(\int\limits_{}^{} {\dfrac{{dx}}{x}} = \ln \left| x \right| + C;\,\,\int\limits_{}^{} {\dfrac{{dx}}{{{x^2}}}} = - \dfrac{1}{x} + C\).
Lời giải chi tiết:
Ta có \(f\left( x \right) = \dfrac{{3x - 2}}{{{{\left( {x - 2} \right)}^2}}} = \dfrac{{3x - 6 + 4}}{{{{\left( {x - 2} \right)}^2}}} = \dfrac{3}{{x - 2}} + \dfrac{4}{{{{\left( {x - 2} \right)}^2}}}\).
\(\begin{array}{l} \Rightarrow \int {f\left( x \right)dx} = \int {\left[ {\dfrac{3}{{x - 2}} + \dfrac{4}{{{{\left( {x - 2} \right)}^2}}}} \right]dx} \\ = 3\int\limits_{}^{} {\dfrac{{dx}}{{x - 2}}} + 4\int\limits_{}^{} {\dfrac{{dx}}{{{{\left( {x - 2} \right)}^2}}}} = 3\ln \left| {x - 2} \right| - \dfrac{4}{{x - 2}} + C\\Do\,\,x \in \left( {2; + \infty } \right) \Rightarrow x - 2 > 0 \Rightarrow \int {f\left( x \right)dx} = 3\ln \left( {x - 2} \right) - \dfrac{4}{{x - 2}} + C\end{array}\)
Chọn D
Câu hỏi 17 :
Họ nguyên hàm của hàm số \(f\left( x \right) = 2x\left( {\sin x + 1} \right)\) là
- A \({x^2} - 2x\cos x + 2\sin x + C\).
- B \({x^2}\left( {x - \cos x} \right) + C\).
- C \({x^2} + 2x\cos x - 2\sin x + C\).
- D \({x^2} - 2x\cos x - 2\sin x + C\).
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp nguyên hàm từng phần.
Lời giải chi tiết:
\(\begin{array}{l}\int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {2x\left( {\sin x + 1} \right)dx} = 2\int\limits_{}^{} {x\sin xdx} + \int\limits_{}^{} {2xdx} = 2{I_1} + {I_2}\\{I_2} = \int\limits_{}^{} {2xdx} = {x^2} + {C_2}\\{I_1} = \int\limits_{}^{} {x\sin xdx} = - \int\limits_{}^{} {xd\left( {\cos x} \right)} = - \left[ {x\cos x - \int\limits_{}^{} {\cos xdx} + {C_1}} \right]\\\,\,\,\,\,\, = - x\cos x + \sin x + {C_1}\\ \Rightarrow \int\limits_{}^{} {f\left( x \right)dx} = - 2x\cos x + 2\sin x + {x^2} + C\end{array}\)
Chọn A.
Câu hỏi 18 :
Cho \(F\left( x \right) = \frac{1}{{2{x^2}}}\) là một nguyên hàm của hàm số \(\frac{{f\left( x \right)}}{x}\). Tìm nguyên hàm của hàm số \(f'\left( x \right)\ln x\).
- A \(\int {f'\left( x \right)\ln xdx} = \frac{{\ln x}}{{{x^2}}} + \frac{1}{{{x^2}}} + C\)
- B \(\int {f'\left( x \right)\ln xdx} = - \left( {\frac{{\ln x}}{{{x^2}}} + \frac{1}{{2{x^2}}}} \right) + C\)
- C \(\int {f'\left( x \right)\ln xdx} = - \left( {\frac{{\ln x}}{{{x^2}}} + \frac{1}{{{x^2}}}} \right) + C\)
- D \(\int {f'\left( x \right)\ln xdx} = \frac{{\ln x}}{{{x^2}}} + \frac{1}{{2{x^2}}} + C\)
Đáp án: B
Phương pháp giải:
- \(F\left( x \right)\) là 1 nguyên hàm của \(f\left( x \right)\) \( \Leftrightarrow F'\left( x \right) = f\left( x \right)\).
- Sử dụng phương pháp nguyên hàm từng phần \(\int {udv} = uv - \int {vdu} \).
Lời giải chi tiết:
\(F\left( x \right) = \frac{1}{{2{x^2}}}\) là một nguyên hàm của hàm số \(\frac{{f\left( x \right)}}{x}\) nên \(\int {\frac{{f\left( x \right)}}{x}dx} = \frac{1}{{2{x^2}}}\).
Và \(\left( {\frac{1}{{2{x^2}}}} \right)' = \frac{{f\left( x \right)}}{x} \Leftrightarrow - \frac{{4x}}{{4{x^4}}} = \frac{{f\left( x \right)}}{x}\) \( \Leftrightarrow f\left( x \right) = - \frac{1}{{{x^2}}}\).
\(I = \int {f'\left( x \right)\ln xdx} \)
Đặt \(\left\{ \begin{array}{l}u = \ln x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{{dx}}{x}\\v = f\left( x \right)\end{array} \right.\)
\(\begin{array}{l} \Rightarrow I = f\left( x \right)\ln x - \int {\frac{{f\left( x \right)dx}}{x}} \\\,\,\,\,\,\,\,\,\,\, = - \frac{1}{{{x^2}}}\ln x - \frac{1}{{2{x^2}}} + C\\\,\,\,\,\,\,\,\,\,\, = - \left( {\frac{{\ln x}}{{{x^2}}} + \frac{1}{{2{x^2}}}} \right) + C\end{array}\)
Chọn B.
Câu hỏi 19 :
Cho \(F\left( x \right) = \dfrac{{{x^2}\ln x}}{a} - \dfrac{{{x^2}}}{b}\) là một nguyên hàm của hàm số \(f\left( x \right) = x.\ln x\) (\(a,b\) là hằng số). Tính \({a^2} - b\)?
- A \(8\)
- B \(0\)
- C \(1\)
- D \(\dfrac{1}{2}\)
Đáp án: B
Phương pháp giải:
- \(F\left( x \right)\) là nguyên hàm của hàm số \(f\left( x \right)\) khi và chỉ khi \(F'\left( x \right) = f\left( x \right).\)
- Sử dụng phương pháp đồng nhất hệ số.
Lời giải chi tiết:
TXĐ:\(D = \left( {0; + \infty } \right)\)
\(F\left( x \right) = \dfrac{{{x^2}\ln x}}{a} - \dfrac{{{x^2}}}{b}\)là nguyên hàm của hàm số \(f\left( x \right) = x\ln x\) nên\(F'\left( x \right) = f\left( x \right)\).
Ta có: \(F\left( x \right) = \dfrac{{{x^2}\ln x}}{a} - \dfrac{{{x^2}}}{b} = \dfrac{1}{a}\left( {{x^2}\ln x} \right) - \dfrac{1}{b}{x^2}.\)
\(\begin{array}{l} \Rightarrow F'\left( x \right) = \dfrac{1}{a}\left( {2x\ln x + {x^2}.\dfrac{1}{x}} \right) - \dfrac{{2x}}{b}\\ \Leftrightarrow F'\left( x \right) = \dfrac{1}{a}.2x\ln x + \dfrac{x}{a} - \dfrac{{2x}}{b} = \dfrac{2}{a}.x\ln x + \left( {\dfrac{1}{a} - \dfrac{2}{b}} \right)x\end{array}\)
Do \(F'\left( x \right) = f\left( x \right)\) nên đồng nhất hệ số ta có: \(\left\{ \begin{array}{l}\dfrac{2}{a} = 1\\\dfrac{1}{a} - \dfrac{2}{b} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 4\end{array} \right.\) .
Vậy \({a^2} - b = {2^2} - 4 = 0.\)
Chọn B.
Câu hỏi 20 :
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}\) trên khoảng \(\left( { - 1; + \infty } \right)\) là:
- A \(2\ln \left( {x + 1} \right) + \frac{2}{{x + 1}} + C\)
- B \(2\ln \left( {x + 1} \right) + \frac{3}{{x + 1}} + C\)
- C \(2\ln \left( {x + 1} \right) - \frac{2}{{x + 1}} + C\)
- D \(2\ln \left( {x + 1} \right) - \frac{3}{{x + 1}} + C\)
Đáp án: B
Phương pháp giải:
Sử dụng phương pháp tìm nguyên hàm của hàm số hữu tỉ với mẫu số có nghiệm kép.
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}I = \int {\frac{{2x - 1}}{{{{\left( {x + 1} \right)}^2}}}dx} = \int {\frac{{2\left( {x + 1} \right) - 3}}{{{{\left( {x + 1} \right)}^2}}}dx} = \int {\frac{2}{{x + 1}}dx - } \int {\frac{3}{{{{\left( {x + 1} \right)}^2}}}dx} \\\,\,\,\, = 2\ln \left| {x + 1} \right| + \frac{3}{{x + 1}} + C = 2\ln \left( {x + 1} \right) + \frac{3}{{x + 1}} + C\,\,\,\,\,\left( {do\,\,x \in \left( { - 1; + \infty } \right) \Rightarrow x + 1 > 0} \right).\end{array}\)
Chọn B.
Câu hỏi 21 :
Cho hàm số \(f\left( x \right)\) thỏa mãn \(f''\left( x \right) = 12{x^2} + 6x - 4\) và \(f\left( 0 \right) = 1,\,\,\,f\left( 1 \right) = 3.\) Tính \(f\left( { - 1} \right).\)
- A \(f\left( { - 1} \right) = - 1.\)
- B \(f\left( { - 1} \right) = - 3.\)
- C \(f\left( { - 1} \right) = 3.\)
- D \(f\left( { - 1} \right) = - 5.\)
Đáp án: B
Phương pháp giải:
Ta có: \(f'\left( x \right) = \int {f''\left( x \right)dx;\,\,\,f\left( x \right) = \int {f'\left( x \right)dx} .} \)
Lời giải chi tiết:
Ta có: \(f''\left( x \right) = 12{x^2} + 6x - 4\)
\(\begin{array}{l} \Rightarrow f'\left( x \right) = \int {\left( {12{x^2} + 6x - 4} \right)dx} = 4{x^3} + 3{x^2} - 4x + C\\ \Rightarrow f\left( x \right) = \int {f'\left( x \right)dx} = \int {\left( {4{x^3} + 3{x^2} - 4x + C} \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {x^4} + {x^3} - 2{x^2} + Cx + C'.\end{array}\)
Lại có: \(\left\{ \begin{array}{l}f\left( 0 \right) = 1\\f\left( 1 \right) = 3\end{array} \right. \Rightarrow \left\{ \begin{array}{l}C' = 1\\1 + 1 - 2 + C + C' = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}C' = 1\\C = 2\end{array} \right..\)
\(\begin{array}{l} \Rightarrow f\left( x \right) = {x^4} + {x^3} - 2{x^2} + 2x + 1.\\ \Rightarrow f\left( { - 1} \right) = {\left( { - 1} \right)^4} + {\left( { - 1} \right)^3} - 2{\left( { - 1} \right)^2} + 2\left( { - 1} \right) + 1 = - 3.\end{array}\)
Chọn B.
Câu hỏi 22 :
Họ tất cả các nguyên hàm của hàm số \(f\left( x \right) = \dfrac{{3x - 1}}{{{{\left( {x - 1} \right)}^2}}}\) trên khoảng \(\left( {1\,;\, + \infty } \right)\) là
- A \(3\ln \left( {x - 1} \right) - \dfrac{2}{{x - 1}} + C\).
- B \(3\ln \left( {x - 1} \right) + \dfrac{1}{{x - 1}} + C\).
- C \(3\ln \left( {x - 1} \right) - \dfrac{1}{{x - 1}} + C\).
- D \(3\ln \left( {x - 1} \right) + \dfrac{2}{{x - 1}} + C\).
Đáp án: A
Phương pháp giải:
Sử dụng các công thức nguyên hàm \(\int {{x^n}dx} = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\) và \(\int {\dfrac{1}{{ax + b}}dx} = \ln \left| {ax + b} \right| + C\)
Lời giải chi tiết:
Ta có
\(\int {f\left( x \right){\rm{d}}x = \int {\dfrac{{3x - 1}}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x} } \)\( = \int {\dfrac{{3\left( {x - 1} \right) + 2}}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x = \int {\left[ {\dfrac{3}{{x - 1}} + \dfrac{2}{{{{\left( {x - 1} \right)}^2}}}} \right]{\rm{d}}x} } \)\( = 3\ln \left| {x - 1} \right| - \dfrac{2}{{x - 1}} + C\)
Xét trên khoảng \(\left( {1\,;\, + \infty } \right)\)ta có \(\left| {x - 1} \right| = x - 1\) nên:
\(\int {f\left( x \right){\rm{d}}x = \int {\dfrac{{3x - 1}}{{{{\left( {x - 1} \right)}^2}}}{\rm{d}}x} } \)\( = 3\ln \left( {x - 1} \right) - \dfrac{2}{{x - 1}} + C\).
Chọn A.
Câu hỏi 23 :
Tìm họ nguyên hàm \(\int {\left( {1 - x} \right){e^{2x}}dx.} \)
- A \(\dfrac{{\left( {1 - 2x} \right){e^{2x}}}}{4} + C\)
- B \(\dfrac{{\left( {3 - 2x} \right){e^{2x}}}}{4} + C\)
- C \(\dfrac{{\left( {3 - 2x} \right){e^{2x}}}}{2} + C\)
- D \(\left( {2 - x} \right){e^{2x}} + C\)
Đáp án: B
Phương pháp giải:
Sử dụng phương pháp nguyên hàm từng phần để làm bài.
Lời giải chi tiết:
Ta có: \(I = \int {\left( {1 - x} \right){e^{2x}}dx} \)
Đặt \(\left\{ \begin{array}{l}u = 1 - x\\dv = {e^{2x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = - dx\\v = \dfrac{1}{2}{e^{2x}}\end{array} \right.\)
\( \Rightarrow I = \dfrac{{\left( {1 - x} \right){e^{2x}}}}{2} + \int {\dfrac{1}{2}{e^{2x}}dx} \) \( = \dfrac{{\left( {1 - x} \right){e^{2x}}}}{2} + \dfrac{1}{4}{e^{2x}} + C = \dfrac{{\left( {3 - 2x} \right){e^{2x}}}}{4} + C.\)
Chọn B.
Câu hỏi 24 :
Tìm họ nguyên hàm \(I = \int {x\sqrt {1 - 2x} dx} .\)
- A \(I = \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^5}} }}{{20}} - \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^3}} }}{{16}} + C.\)
- B \(I = \dfrac{{\left( {3x + 1} \right)\sqrt {{{\left( {1 - 2x} \right)}^3}} }}{{15}} + C.\)
- C \(I = \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^5}} }}{{10}} - \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^3}} }}{6}.\)
- D \(I = \dfrac{{\left( {3x + 1} \right)\sqrt {{{\left( {1 - 2x} \right)}^3}} }}{{15}} + C.\)
Đáp án: C
Phương pháp giải:
Sử dụng phương pháp đổi biến để làm bài.
Lời giải chi tiết:
Ta có: \(I = \int {x\sqrt {1 - 2x} dx} .\)
Đặt \(t = \sqrt {1 - 2x} \Rightarrow {t^2} = 1 - 2x \Rightarrow 2tdt = - 2dx \Rightarrow dx = - tdt.\)
\(\begin{array}{l} \Rightarrow x = \dfrac{{1 - {t^2}}}{2}.\\ \Rightarrow I = - \int {\dfrac{{1 - {t^2}}}{2}.{t^2}dt} = \dfrac{1}{2}\int {\left( {{t^4} - {t^2}} \right)dt} = \dfrac{1}{2}\left( {\dfrac{{{t^5}}}{5} - \dfrac{{{t^3}}}{3}} \right) + C\\ = \dfrac{{{t^5}}}{{10}} - \dfrac{{{t^3}}}{6} + C = \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^5}} }}{{10}} - \dfrac{{\sqrt {{{\left( {1 - 2x} \right)}^3}} }}{6} + C.\end{array}\)
Chọn C.
Câu hỏi 25 :
Cho hàm số \(f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ {\dfrac{1}{2}} \right\}\) thỏa mãn \(f'\left( x \right) = \dfrac{2}{{2x - 1}}\), \(f\left( 0 \right) = 1\) và \(f\left( 1 \right) = 2\). Giá trị của biểu thức \(f\left( { - 1} \right) + f\left( 3 \right)\) bằng:
- A \(4 + \ln 15\)
- B \(2 + \ln 15\)
- C \(3 + \ln 15\)
- D \(\ln 15\)
Đáp án: C
Phương pháp giải:
- Sử dụng công thức \(f\left( x \right) = \int {f'\left( x \right)dx} \).
- Phá trị tuyệt đối, tìm hằng số \(C\) trong từng trường hợp.
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = \dfrac{2}{{2x - 1}}\)
\( \Rightarrow f\left( x \right) = \int {\dfrac{2}{{2x - 1}}dx} = \ln \left| {2x - 1} \right| + C\)\( = \left[ \begin{array}{l}\ln \left( {2x - 1} \right) + {C_1}\,\,\,khi\,\,x \ge \dfrac{1}{2}\\\ln \left( {1 - 2x} \right) + {C_2}\,\,\,khi\,\,x < \dfrac{1}{2}\end{array} \right.\).
Với \(x = 0\) ta có \(f\left( 0 \right) = \ln 1 + {C_2} = 1\)\( \Rightarrow {C_2} = 1\).
Với \(x = 1\) ta có \(f\left( 1 \right) = \ln 1 + {C_1} = 2 \Rightarrow {C_1} = 2\).
\(\begin{array}{l} \Rightarrow f\left( x \right) = \left[ \begin{array}{l}\ln \left( {2x - 1} \right) + 2\,\,\,khi\,\,x \ge \dfrac{1}{2}\\\ln \left( {1 - 2x} \right) + 1\,\,\,khi\,\,x < \dfrac{1}{2}\end{array} \right.\\ \Rightarrow f\left( { - 1} \right) = \ln 3 + 1;\,\,f\left( 3 \right) = \ln 5 + 2\\ \Rightarrow f\left( { - 1} \right) + f\left( 3 \right) = \ln 3 + \ln 5 + 3 = 3 + ln15\end{array}\)
Chọn C.
Câu hỏi 26 :
\(\int {{{4x - 1} \over {4{x^2} - 2x + 5}}dx} \) bằng?
- A \({1 \over 2}\ln \left( {4{x^2} - 2x + 5} \right) + C\)
- B \( - {1 \over {4{x^2} - 2x + 5}} + C\)
- C \({1 \over {4{x^2} - 2x + 5}} + C\)
- D \( - \ln \left( {4{x^2} - 2x + 5} \right) + C\)
Đáp án: A
Lời giải chi tiết:
Hướng dẫn giải chi tiết
\(F\left( x \right) = \int {{{4x - 1} \over {4{x^2} - 2x + 5}}dx} \)
Ta có: \(4{x^2} - 2x + 5 = {\left( {2x} \right)^2} - 2.\left( {2x} \right).{1 \over 2} + {1 \over 4} + {{19} \over 4} = {\left( {2x - {1 \over 2}} \right)^2} + {{19} \over 4}\) \( \Rightarrow F\left( x \right) = \int {{{2\left( {2x - {1 \over 2}} \right)} \over {{{\left( {2x - {1 \over 2}} \right)}^2} + {{19} \over 4}}}dx} \)
Đặt \(2x - {1 \over 2} = {{\sqrt {19} } \over 2}\tan t \Rightarrow 2dx = {{\sqrt {19} } \over 2}{{dt} \over {{{\cos }^2}t}} = {{\sqrt {19} } \over 2}\left( {1 + {{\tan }^2}t} \right)dt\)
\(\eqalign{ & \Rightarrow F\left( t \right) = \int {{{{{\sqrt {19} } \over 2}\tan t} \over {{{19} \over 4}\left( {{{\tan }^2}t + 1} \right)}}{{\sqrt {19} } \over 2}\left( {1 + {{\tan }^2}t} \right)dt} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int {\tan tdt} = \int {{{\sin t} \over {\cos t}}dt} = - \int {{{d\left( {\cos t} \right)} \over {\cos t}}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = - \ln \left| {\cos t} \right| + C\,\,\,\left( {C = const} \right) \cr} \)
Ta có:
\(\eqalign{ & 2x - {1 \over 2} = {{\sqrt {19} } \over 2}\tan t \Rightarrow \tan t = {2 \over {\sqrt {19} }}\left( {2x - {1 \over 2}} \right) \Rightarrow {\tan ^2}t + 1 = {4 \over {19}}{\left( {2x - {1 \over 2}} \right)^2} + 1 = {1 \over {{{\cos }^2}t}} \cr & \Rightarrow {\cos ^2}t = {1 \over {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1}} \Rightarrow \cos t = \sqrt {{1 \over {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1}}} = {1 \over {\sqrt {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1} }} \cr & \Rightarrow F\left( x \right) = - \ln {1 \over {\sqrt {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1} }} + C = \ln \sqrt {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1} + C = {1 \over 2}\ln \left( {{4 \over {19}}{{\left( {2x - {1 \over 2}} \right)}^2} + 1} \right) + C \cr & = {1 \over 2}\ln \left[ {{4 \over {19}}\left( {{{\left( {2x - {1 \over 2}} \right)}^2} + {{19} \over 4}} \right)} \right] = {1 \over 2}\ln {4 \over {19}} + {1 \over 2}\ln \left[ {{{\left( {2x - {1 \over 2}} \right)}^2} + {{19} \over 4}} \right] + C \cr & = {1 \over 2}\ln \left( {4{x^2} - 2x + 5} \right) + C'\,\,\,\,\,\left( {C' = C + {1 \over 2}\ln {4 \over {19}} = const} \right) \cr} \)
Chọn A.
Câu hỏi 27 :
Xét nguyên hàm \(I = \int {{x^2}{e^{3{x^3}}}dx} \). Đặt \(3{x^3} = u\) thu được \(I = m{e^u} + C\). Tính giá trị \(m ?\)
- A \(1 \over 9\)
- B \(10 \over 9\)
- C \(11 \over 9\)
- D \(22 \over 3\)
Đáp án: A
Lời giải chi tiết:
Hướng dẫn giải chi tiết.
\(I = \int {{x^2}{e^{3{x^3}}}dx} \)
Đặt \(3{x^3} = u \Rightarrow 9{x^2}dx = du \Rightarrow {x^2}dx = {{du} \over 9}\)
\(I = \int {{{{e^u}du} \over 9}} = {1 \over 9}{e^u} + C \Rightarrow m = {1 \over 9}\)
Chọn A.
Câu hỏi 28 :
Cho a,b là hai số nguyên dương và nguyên tố cùng nhau. Hàm số \(F(x) = {a \over {b\cos x}} - 1\) là một nguyên hàm của hàm số \(f(x) = {{{\mathop{\rm s}\nolimits} {\rm{inx}}} \over {2{{\cos }^2}x}}\). Trong các mệnh đề sau, mệnh đề nào đúng?
- A \( 2a-b>0 \)
- B \(2a-b<0\)
- C \(3a-b<0\)
- D \(a+b=3\)
Đáp án: D
Lời giải chi tiết:
\(F\left( x \right) = \int {f(x)dx} = \int {{{{\mathop{\rm s}\nolimits} {\rm{inx}}} \over {2{{\cos }^2}x}}dx} \)
Đặt \(t = \cos x \Rightarrow dt = - \sin xdx \Rightarrow \sin xdx = - dt\)
\(\eqalign{ & \Rightarrow F\left( x \right) = - \int {{{dt} \over {2{t^2}}}} = - {1 \over 2}.\left( { - {1 \over t}} \right) + C = {1 \over {2t}} + C = {1 \over {2\cos x}} + C = {a \over {b\cos x}} - 1 \cr & \Rightarrow \left\{ \matrix{a = 1 \hfill \cr b = 2 \hfill \cr C = - 1 \hfill \cr} \right.\,\,\left( {tm} \right) \cr} \)
Ta có: \(2a - b = 2 - 2 = 0 \Rightarrow \) A và B sai
\(3a - b = 3 - 2 = 1 > 0 \Rightarrow C\) sai
Chọn D.
Câu hỏi 29 :
Giả sử một nguyên hàm của hàm số \(f\left( x \right) = {{{x^2}} \over {\sqrt {1 - {x^3}} }} + {1 \over {\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}\) có dạng \(A\sqrt {1 - {x^3}} + {B \over {1 + \sqrt x }}\). Hãy tính A + B.
- A \(A + B = - 2\)
- B \(A + B = {8 \over 3}\)
- C \(A + B = 2\)
- D \(A + B = - {8 \over 3}\)
Đáp án: D
Phương pháp giải:
\(\int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {{{{x^2}} \over {\sqrt {1 - {x^3}} }}dx} + \int\limits_{}^{} {{1 \over {\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}dx} = {I_1} + {I_2}\)
Với I1 đặt \(t = \sqrt {1 - {x^3}} \), I2 đặt \(t = 1 + \sqrt x \)
Lời giải chi tiết:
\(\int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {{{{x^2}} \over {\sqrt {1 - {x^3}} }}dx} + \int\limits_{}^{} {{1 \over {\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}dx} = {I_1} + {I_2}\)
Xét \({I_1} = \int\limits_{}^{} {{{{x^2}} \over {\sqrt {1 - {x^3}} }}dx} \). Đặt \(t = \sqrt {1 - {x^3}} \Leftrightarrow {t^2} = 1 - {x^3} \Leftrightarrow 2tdt = - 3{x^2}dx \Rightarrow {x^2}dx = - {2 \over 3}tdt\)
\( \Rightarrow {I_1} = \int\limits_{}^{} {{{ - {2 \over 3}tdt} \over t}} = {{ - 2} \over 3}t + C = - {2 \over 3}\sqrt {1 - {x^3}} + C\)
Xét \({I_2} = \int\limits_{}^{} {{1 \over {\sqrt x {{\left( {1 + \sqrt x } \right)}^2}}}dx} \), đặt \(t = 1 + \sqrt x \Rightarrow dt = {1 \over {2\sqrt x }}dx \Rightarrow {{dx} \over {\sqrt x }} = 2dt\)
\(\eqalign{ & \Rightarrow {I_2} = \int\limits_{}^{} {{{2dt} \over {{t^2}}}} = - {2 \over t} + C = - {2 \over {1 + \sqrt x }} + C \cr & \Rightarrow I = - {2 \over 3}\sqrt {1 - {x^3}} - {2 \over {1 + \sqrt x }} + C \cr & \Rightarrow \left\{ \matrix{ A = - {2 \over 3} \hfill \cr B = - 2 \hfill \cr} \right. \Rightarrow A + B = - {8 \over 3} \cr} \).
Chọn D.
Câu hỏi 30 :
Gọi \(F\left( x \right)\) là một nguyên hàm của hàm số \(f\left( x \right) = {x \over {\sqrt {8 - {x^2}} }}\) thỏa mãn \(F\left( 2 \right) = 0\). Khi đó phương trình \(F\left( x \right) = x\) có tổng tất cả các nghiệm bằng :
- A \(1 + \sqrt 3 \)
- B 2
- C 1
- D \(1 - \sqrt 3 \)
Đáp án: D
Phương pháp giải:
Đặt \(t = \sqrt {8 - {x^2}} \)
Lời giải chi tiết:
Đặt \(t = \sqrt {8 - {x^2}} \Leftrightarrow {t^2} = 8 - {x^2} \Leftrightarrow tdt = - xdx \Rightarrow xdx = - tdt\)
\(\eqalign{ & \Rightarrow F\left( x \right) = \int\limits_{}^{} {f\left( x \right)dx} = \int\limits_{}^{} {{x \over {\sqrt {8 - {x^2}} }}dx} = \int\limits_{}^{} {{{ - tdt} \over t}} = - t + C = - \sqrt {8 - {x^2}} + C \cr & F\left( 2 \right) = 0 \Leftrightarrow - 2 + C = 0 \Rightarrow C = 2 \cr & \Rightarrow F\left( x \right) = - \sqrt {8 - {x^2}} + 2 \cr & F\left( x \right) = x \Leftrightarrow - \sqrt {8 - {x^2}} + 2 = x \cr & \Leftrightarrow \sqrt {8 - {x^2}} = 2 - x \cr & \Leftrightarrow \left\{ \matrix{ 2 - x \ge 0 \hfill \cr 8 - {x^2} = {x^2} - 4x + 4 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{ x \le 2 \hfill \cr 2{x^2} - 4x - 4 = 0 \hfill \cr} \right. \Leftrightarrow x = 1 - \sqrt 3 \cr} \)
Vậy phương trình \(F\left( x \right) = x\) có nghiệm duy nhất \(x = 1 - \sqrt 3 \)
Chọn D.
Câu hỏi 31 :
Cho hàm số \(f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\) và thỏa mãn đồng thời các điều kiện sau
\(f\left( x \right)>0;\,\,\,{f}'\left( x \right)=\frac{x.f\left( x \right)}{\sqrt{{{x}^{2}}+1}};\,\,\forall x\in \mathbb{R}\) và \(f\left( 0 \right)=e.\) Giá trị của \(f\left( \sqrt{3} \right)\) bằng
- A \({{e}^{-\,1}}.\)
- B \({{e}^{\,2}}.\)
- C \(e.\)
- D \({{e}^{-\,2}}.\)
Đáp án: B
Phương pháp giải:
Chia biểu thức, lấy nguyên hàm hai vế để tìm được hàm số \(f \left(x\right).\)
Lời giải chi tiết:
Ta có \({f}'\left( x \right)=\frac{x.f\left( x \right)}{\sqrt{{{x}^{2}}+1}}\Leftrightarrow \frac{{f}'\left( x \right)}{f\left( x \right)}=\frac{x}{\sqrt{{{x}^{2}}+1}}\Leftrightarrow \int{\frac{{f}'\left( x \right)}{f\left( x \right)}\text{d}x}=\int{\frac{x}{\sqrt{{{x}^{2}}+1}}\text{d}x}\)
\(\Leftrightarrow \int{\frac{\text{d}\left( f\left( x \right) \right)}{f\left( x \right)}}=\int{\frac{\text{d}\left( {{x}^{2}}+1 \right)}{2\sqrt{{{x}^{2}}+1}}}=\sqrt{{{x}^{2}}+1}+C\Leftrightarrow \ln f\left( x \right)=\sqrt{{{x}^{2}}+1}+C\Leftrightarrow f\left( x \right)={{e}^{\sqrt{{{x}^{2}}\,+\,1}\,+\,\,C}}\)
Mà \(f\left( 0 \right)=e\) \(\xrightarrow{{}}\) \({{e}^{C\,+\,1}}=e\Rightarrow C=0.\) Vậy \(f\left( \sqrt{3} \right)={{e}^{2}}.\)
Chọn B
Câu hỏi 32 :
Cho hàm số \(f(x)\) thỏa mãn \({{\left( {f}'(x) \right)}^{2}}+f(x).{{f}'}'(x)=15{{x}^{4}}+12x,\,\,\forall x\in R\) và \(f(0)={f}'(0)=1.\) Giá trị của \({{f}^{2}}(1)\) bằng
- A \(4\)
- B \(\frac{9}{2}.\)
- C \(10.\)
- D \(\frac{5}{2}.\)
Đáp án: A
Phương pháp giải:
+) Nhận xét \(VT=\left[ f\left( x \right).f'\left( x \right) \right]'\) .
+) Lấy nguyên hàm hai vế hai lần.
Lời giải chi tiết:
Ta có \(\left[ f\left( x \right).f'\left( x \right) \right]'={{\left[ f'\left( x \right) \right]}^{2}}+f\left( x \right).f''\left( x \right)=15{{x}^{4}}+12x\)
Nguyên hàm 2 vế ta được \(f\left( x \right).f'\left( x \right)=3{{x}^{5}}+6{{x}^{2}}+C\)
Do \(f\left( 0 \right)=f'\left( 0 \right)=1\Rightarrow C=1\)
Tiếp tục nguyên hàm 2 vế ta được: \(\int{f\left( x \right)df\left( x \right)}=\int{\left( 3{{x}^{5}}+6{{x}^{2}}+1 \right)dx}\)
\(\Rightarrow \frac{{{f}^{2}}\left( x \right)}{2}=\frac{3{{x}^{6}}}{6}+\frac{6{{x}^{3}}}{3}+x+D=\frac{1}{2}{{x}^{6}}+2{{x}^{3}}+x+D\).
Do \(f\left( 0 \right)=1\Rightarrow D=\frac{1}{2}\Rightarrow {{f}^{2}}\left( x \right)=\frac{1}{2}{{x}^{6}}+2{{x}^{3}}+x+\frac{1}{2}\Rightarrow {{f}^{2}}\left( 1 \right)=4\)
Chọn A.
Câu hỏi 33 :
Cho hàm số \(f\left( x \right)\) liên tục trên R và \(f\left( x \right)\ne 0\) với mọi \(x\in R\). \(f'\left( x \right)=\left( 2x+1 \right){{f}^{2}}\left( x \right)\) và \(f\left( 1 \right)=-0.5\). Biết rằng tổng \(f\left( 1 \right)+f\left( 2 \right)+f\left( 3 \right)+...+f\left( 2017 \right)=\frac{a}{b};\,\,\left( a\in Z,b\in N \right)\) với \(\frac{a}{b}\) tối giản.Mệnh đề nào dưới đây đúng?
- A \(a\in \left( -2017;2017 \right)\)
- B \(b-a=4035\)
- C \(a+b=-1\)
- D \(\frac{a}{b}<-1\)
Đáp án: B
Phương pháp giải:
Chuyển vế, lấy nguyên hàm hai vế.
Lời giải chi tiết:
\(\begin{array}{l}
\,\,\,\,\,f'\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right)\\
\Leftrightarrow \frac{{f'\left( x \right)}}{{{f^2}\left( x \right)}} = 2x + 1\\
\Leftrightarrow \int\limits_{}^{} {\frac{{f'\left( x \right)dx}}{{{f^2}\left( x \right)}}} = \int\limits_{}^{} {\left( {2x + 1} \right)dx} \\
\Leftrightarrow \frac{{ - 1}}{{f\left( x \right)}} = {x^2} + x + C\\
f\left( 1 \right) = - 0,5 \Leftrightarrow - \frac{1}{{ - 0,5}} = 1 + 1 + C \Leftrightarrow C = 0\\
\Leftrightarrow f\left( x \right) = - \frac{1}{{{x^2} + x}} = - \frac{1}{{x\left( {x + 1} \right)}} = - \left( {\frac{1}{x} - \frac{1}{{x + 1}}} \right) = \frac{1}{{x + 1}} - \frac{1}{x}\\
\Rightarrow f\left( 1 \right) + f\left( 2 \right) + f\left( 3 \right) + ... + f\left( {2017} \right)\\
= \frac{1}{2} - 1 + \frac{1}{3} - \frac{1}{2} + \frac{1}{4} - \frac{1}{3} + ... + \frac{1}{{2017}} - \frac{1}{{2016}} + \frac{1}{{2018}} - \frac{1}{{2017}}\\
= - 1 + \frac{1}{{2018}} = \frac{{ - 2017}}{{2018}} = \frac{a}{b} \Rightarrow \left\{ \begin{array}{l}
a = - 2017\\
b = 2018
\end{array} \right. \Rightarrow b - a = 4035
\end{array}\)
Chọn B.
Câu hỏi 34 :
Tính \(\int {{{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} \)?
- A \({x \over {{x^2} + 1}} + C\)
- B \({{2x} \over {{x^2} + 1}} + C\)
- C \({{ - x} \over {{x^2} + 1}} + C\)
- D \({{ - 2x} \over {{x^2} + 1}} + C\)
Đáp án: C
Phương pháp giải:
Nhận xét \({{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}} = {{2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}} - {1 \over {{x^2} + 1}} \Rightarrow \int {{{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} = \int {{{2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} - \int {{1 \over {{x^2} + 1}}dx} .\)
Sử dụng phương pháp tích phần từng phần để tính tích phân thứ nhất, đặt \(\left\{ \matrix{ u = x \hfill \cr dv = {{d\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} + 1} \right)}^2}}} \hfill \cr} \right.\)
Lời giải chi tiết:
Ta có: \({{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}} = {{2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}} - {1 \over {{x^2} + 1}} \Rightarrow \int {{{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} = \int {{{2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} - \int {{1 \over {{x^2} + 1}}dx} \,\,\left( 1 \right)\)
Ta tính \(\int {{{2{x^2}} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} = \int {{{xd\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} + 1} \right)}^2}}}} \) bằng phương pháp tích phân từng phân như sau:
Đặt \(\left\{ \matrix{ u = x \hfill \cr dv = {{d\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} + 1} \right)}^2}}} \hfill \cr} \right. \Rightarrow \left\{ \matrix{ du = dx \hfill \cr v = - {1 \over {{x^2} + 1}} \hfill \cr} \right. \Rightarrow \int {{{xd\left( {{x^2} + 1} \right)} \over {{{\left( {{x^2} + 1} \right)}^2}}}} = - {x \over {{x^2} + 1}} + \int {{{dx} \over {{x^2} + 1}}} + C\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(\int {{{{x^2} - 1} \over {{{\left( {{x^2} + 1} \right)}^2}}}dx} = - {x \over {{x^2} + 1}} + \int {{{dx} \over {{x^2} + 1}}} + C - \int {{1 \over {{x^2} + 1}}dx} = - {x \over {{x^2} + 1}} + C.\)
Chọn C.
Câu hỏi 35 :
Cho hàm số \(y=f\left( x \right)=a{{x}^{3}}+b{{x}^{2}}+cx+d\,\,\left( a;b;c;d\in R,\,\,a\ne 0 \right)\) có đồ thị \(\left( C \right)\). Biết rằng đồ thị \(\left( C \right)\) đi qua gốc tọa độ và có đồ thị hàm số \(y=f'\left( x \right)\) cho bởi hình vẽ sau đây.
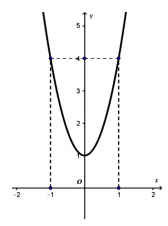
Tính giá trị \(H=f\left( 4 \right)-f\left( 2 \right)\).
- A
\(H=51\)
- B
\(H=45\)
- C
\(H=58\)
- D \(H=64\)
Đáp án: C
Phương pháp giải:
Xác định hàm số \(f'\left( x \right)\) từ đó tính được \(f\left( x \right)=\int\limits_{{}}^{{}}{f'\left( x \right)dx}\).
Lời giải chi tiết:
Ta dễ dàng tìm được phương trình parabol là \(y=3{{x}^{2}}+1\Rightarrow f'\left( x \right)=3{{x}^{2}}+1\Rightarrow f\left( x \right)=\int\limits_{{}}^{{}}{f'\left( x \right)dx}={{x}^{3}}+x+C\)
Đồ thị hàm số đi qua gốc tọa độ \(\Rightarrow C=0\Rightarrow f\left( x \right)={{x}^{3}}+x\)
\(\Rightarrow f\left( 4 \right)=68;\,\,f\left( 2 \right)=10\Rightarrow H=58\).
Chọn C.
Câu hỏi 36 :
Cho hàm số \(f\left( x \right)\) thỏa mãn \({\left[ {f'\left( x \right)} \right]^2} + f\left( x \right).f''\left( x \right) = {x^3} - 2x\;\;\forall x \in R\) và \(f\left( 0 \right) = f'\left( 0 \right) = 2.\) Tính giá trị của \(T = {f^2}\left( 2 \right).\)
- A \(\dfrac{{268}}{{15}}\)
- B \(\dfrac{{160}}{{15}}\)
- C \(\dfrac{{268}}{{30}}\)
- D \(\dfrac{4}{{15}}\)
Đáp án: A
Phương pháp giải:
+) Dựa vào phương trình đã cho của bài toán ta có thể thấy: \(VT = \left[ {f\left( x \right).f'\left( x \right)} \right]'.\)
+) Lấy nguyên hàm hai vế và dựa vào giả thiết bài toán để làm tiếp.
Lời giải chi tiết:
Ta có: \(VT = \left[ {f\left( x \right).f'\left( x \right)} \right]' = f'\left( x \right).f'\left( x \right) + f\left( x \right).f''\left( x \right) = {\left[ {f'\left( x \right)} \right]^2} + f\left( x \right).f''\left( x \right)\)
\( \Rightarrow \left[ {f'\left( x \right).f\left( x \right)} \right]' = {x^3} - 2x\;\;\;\left( * \right)\)
Nguyên hàm hai vế của \(\left( * \right)\) ta được: \(f'\left( x \right).f\left( x \right) = \dfrac{{{x^4}}}{4} - {x^2} + C.\;\;\left( 1 \right)\)
Lại có: \(f'\left( 0 \right) = f\left( 0 \right) = 2 \Rightarrow C = 2.2 = 4.\)
\(\begin{array}{l} \Rightarrow \left( 1 \right) \Leftrightarrow f\left( x \right).f'\left( x \right) = \dfrac{{{x^4}}}{4} - {x^2} + 4\\ \Rightarrow \int {f\left( x \right)f'\left( x \right)dx = \int {\left( {\dfrac{{{x^4}}}{4} - {x^2} + 4} \right)} } dx \Leftrightarrow \int {f\left( x \right)df\left( x \right) = \dfrac{{{x^5}}}{{20}} - \dfrac{{{x^3}}}{3} + 4x + A} \\ \Leftrightarrow \dfrac{{{f^2}\left( x \right)}}{2} = \dfrac{{{x^5}}}{{20}} - \dfrac{{{x^3}}}{3} + 4x + A \Leftrightarrow {f^2}\left( x \right) = \dfrac{{{x^5}}}{{10}} - \dfrac{{2{x^3}}}{3} + 8x + 2A.\end{array}\)
Có \(f\left( 0 \right) = 2 \Rightarrow 4 = 2A \Leftrightarrow A = 2\)
\(\begin{array}{l} \Rightarrow {f^2}\left( x \right) = \dfrac{{{x^5}}}{{10}} - \dfrac{{2{x^3}}}{3} + 8x + 4\\ \Rightarrow {f^2}\left( 2 \right) = \dfrac{{{2^5}}}{{10}} - \dfrac{{{{2.2}^3}}}{3} + 8.2 + 4 = \dfrac{{268}}{{15}}.\end{array}\)
Chọn A.
Câu hỏi 37 :
Cho hàm số \(f\left( x \right) > 0\) với mọi \(x \in R\), \(f\left( 0 \right) = 1\) và \(f\left( x \right) = \sqrt {x + 1} f'\left( x \right)\) với mọi \(x \in R\). Mệnh đề nào dưới đây đúng?
- A \(4 < f\left( 3 \right) < 6\)
- B \(f\left( 3 \right) < 2\)
- C \(2 < f\left( 3 \right) < 4\)
- D \(f\left( 3 \right) > 6\)
Đáp án: D
Phương pháp giải:
+) Từ giải thiết suy ra \(\frac{{f'\left( x \right)}}{{f\left( x \right)}} = \frac{1}{{\sqrt {x + 1} }}\)
+) Sử dụng phương pháp nguyên hàm 2 vế.
Lời giải chi tiết:
Theo bài ra ta có: \(f\left( x \right) = \sqrt {x + 1} f'\left( x \right)\) (*).
Do \(f\left( x \right) > 0\,\,\forall x \in R\) nên từ (*) ta có \(\frac{{f'\left( x \right)}}{{f\left( x \right)}} = \frac{1}{{\sqrt {x + 1} }}\).
Lấy nguyên hàm 2 vế ta được: \(\int\limits_{}^{} {\frac{{f'\left( x \right)}}{{f\left( x \right)}}dx} = \int\limits_{}^{} {\frac{1}{{\sqrt {x + 1} }}dx} \)
\( \Leftrightarrow \ln \left| {f\left( x \right)} \right|dx = 2\sqrt {x + 1} + C \Leftrightarrow \ln f\left( x \right) = 2\sqrt {x + 1} + C \Leftrightarrow f\left( x \right) = {e^{2\sqrt {x + 1} + C}}\)
Ta có \(f\left( 0 \right) = 1 \Rightarrow 1 = {e^{2 + C}} \Leftrightarrow 2 + C = 0 \Leftrightarrow C = - 2\).
Do đó \(f\left( x \right) = {e^{2\sqrt {x + 1} - 2}} \Rightarrow f\left( 3 \right) = {e^2} \approx 7,4 > 6\).
Chọn D.
Câu hỏi 38 :
Cho \(f\left( x \right)=\frac{x}{{{\cos }^{2}}x}\) trên \(\left( -\frac{\pi }{2};\frac{\pi }{2} \right)\) và \(F\left( x \right)\) là một nguyên hàm của hàm số \(xf'\left( x \right)\) thỏa mãn \(F\left( 0 \right)=0\). Biết \(a\in \left( -\frac{\pi }{2};\frac{\pi }{2} \right)\) thỏa mãn \(\tan a=3\). Tính \(F\left( a \right)-10{{a}^{2}}+3a\).
- A
\(\frac{1}{2}\ln 10\)
- B
\(-\frac{1}{4}\ln 10\)
- C
\(-\frac{1}{2}\ln 10\)
- D \(\ln 10\)
Đáp án: A
Phương pháp giải:
Sử dụng phương pháp tích phân từng phần tính \(F\left( x \right)\).
Lời giải chi tiết:
Theo bài ra ta có: \(F\left( x \right) = \int {xf\left( x \right)dx} \).
Đặt \(\left\{ \begin{array}{l}u = x\\dv = f'\left( x \right)dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = f\left( x \right)\end{array} \right.\).
Khi đó ta có:
\(\begin{array}{*{20}{l}}\begin{array}{l}F\left( x \right) = x.f\left( x \right) - \int {f\left( x \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - \int\limits_{}^{} {\frac{x}{{{{\cos }^2}x}}dx} + C\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - \int\limits_{}^{} {xd\left( {\tan x} \right)} + C\end{array}\\\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x + \int\limits_{}^{} {\tan dx} + C\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x + \int\limits_{}^{} {\frac{{\sin x}}{{\cos x}}dx} + C\end{array}\\\begin{array}{l}\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \int\limits_{}^{} {\frac{{d\left( {\cos x} \right)}}{{\cos x}}} + C\\\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \ln \left| {\cos x} \right| + C\end{array}\\{F\left( 0 \right) = C = 0 \Rightarrow F\left( x \right) = \frac{{{x^2}}}{{{{\cos }^2}x}} - x\tan x - \ln \left| {\cos x} \right|}\\{F\left( x \right) = \int\limits_{}^{} {xf'\left( x \right)dx} = \int\limits_{}^{} {xd\left( {f\left( x \right)} \right)} = xf\left( x \right) - \int\limits_{}^{} {f\left( x \right)dx} + C}\\\begin{array}{l}\tan a = 3 \Rightarrow \frac{1}{{{{\cos }^2}a}} = {\tan ^2}a + 1 = 10\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \Leftrightarrow \cos a = \frac{1}{{\sqrt {10} }}\left( {a \in \left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)} \right)\end{array}\end{array}\)
\(\begin{array}{l} \Rightarrow F\left( a \right) = 10{a^2} - 3a - \ln \frac{1}{{\sqrt {10} }}\\ \Rightarrow F\left( a \right) - 10{a^2} + 3a = - \ln \frac{1}{{\sqrt {10} }} = - \frac{1}{2}\ln \frac{1}{{10}} = \frac{1}{2}\ln 10\end{array}\)
Chọn A.
Câu hỏi 39 :
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;4} \right]\) thỏa mãn \(f''\left( x \right)f\left( x \right) + \frac{{{{\left[ {f\left( x \right)} \right]}^2}}}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}} = {\left[ {f'\left( x \right)} \right]^2}\) và \(f\left( x \right) > 0\) với mọi \(x \in \left[ {0;4} \right]\). Biết rằng \(f'\left( 0 \right) = f\left( 0 \right) = 1\), giá trị của \(f\left( 4 \right)\) bằng:
- A \({e^2}\)
- B \(2e\)
- C \({e^3}\)
- D \({e^2} + 1\)
Đáp án: A
Lời giải chi tiết:
\(\begin{array}{l}f''\left( x \right)f\left( x \right) + \frac{{{{\left[ {f\left( x \right)} \right]}^2}}}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}} = {\left[ {f'\left( x \right)} \right]^2}\\ \Leftrightarrow f''\left( x \right)f\left( x \right) - {\left[ {f'\left( x \right)} \right]^2} = - \frac{{{{\left[ {f\left( x \right)} \right]}^2}}}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}}\\ \Leftrightarrow \frac{{f''\left( x \right)f\left( x \right) - {{\left[ {f'\left( x \right)} \right]}^2}}}{{{{\left[ {f\left( x \right)} \right]}^2}}} = - \frac{1}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}}\\ \Leftrightarrow \left[ {\frac{{f'\left( x \right)}}{{f\left( x \right)}}} \right]' = - \frac{1}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}}\\ \Leftrightarrow \frac{{f'\left( x \right)}}{{f\left( x \right)}} = - \int\limits_{}^{} {\frac{{dx}}{{{{\sqrt {\left( {2x + 1} \right)} }^3}}}} = - \int\limits_{}^{} {{{\left( {2x + 1} \right)}^{ - \frac{3}{2}}}dx} \\ \Leftrightarrow \frac{{f'\left( x \right)}}{{f\left( x \right)}} = - \frac{{{{\left( {2x + 1} \right)}^{ - \frac{1}{2}}}}}{{ - \frac{1}{2}.2}} + C = {\left( {2x + 1} \right)^{ - \frac{1}{2}}} + C\end{array}\)
Thay \(x = 0\) ta có: \(\frac{{f'\left( 0 \right)}}{{f\left( 0 \right)}} = 1 + C \Leftrightarrow 1 = 1 + C \Leftrightarrow C = 0 \Rightarrow \Leftrightarrow \frac{{f'\left( x \right)}}{{f\left( x \right)}} = {\left( {2x + 1} \right)^{ - \frac{1}{2}}}\).
Lấy nguyên hàm 2 vế ta có:
\(\int\limits_{}^{} {\frac{{f'\left( x \right)}}{{f\left( x \right)}}dx} = \int\limits_{}^{} {{{\left( {2x + 1} \right)}^{ - \frac{1}{2}}}dx} \Leftrightarrow \ln \left| {f\left( x \right)} \right| = \frac{{{{\left( {2x + 1} \right)}^{\frac{1}{2}}}}}{{\frac{1}{2}.2}} + C = {\left( {2x + 1} \right)^{\frac{1}{2}}} + C\).
Do \(f\left( x \right) > 0\,\,\forall x \in \left[ {0;4} \right] \Rightarrow \ln f\left( x \right) = {\left( {2x + 1} \right)^{\frac{1}{2}}} + C\).
Thay \(x = 0\) ta có \(\ln f\left( 0 \right) = 1 + C \Leftrightarrow \ln 1 = 1 + C \Leftrightarrow 1 + C = 0 \Leftrightarrow C = - 1\).
\( \Rightarrow \ln f\left( x \right) = {\left( {2x + 1} \right)^{\frac{1}{2}}} - 1 \Leftrightarrow f\left( x \right) = {e^{{{\left( {2x + 1} \right)}^{\frac{1}{2}}} - 1}} \Rightarrow f\left( 4 \right) = {e^{3 - 1}} = {e^2}\).
Chọn A.
Câu hỏi 40 :
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R},\,\,f\left( x \right) \ne 0\) với mọi \(x\) và thỏa mãn \(f\left( 1 \right) = - \frac{1}{2},\) \(f'\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right).\) Biết \(f\left( 1 \right) + f\left( 2 \right) + ...... + f\left( {2019} \right) = \frac{a}{b} - 1\) với \(a \in \mathbb{Z},\,\,b \in \mathbb{N},\,\,\left( {a;\,b} \right) = 1.\)
Khẳng định nào say đây là sai?
- A \(a - b = 2019\)
- B \(ab > 2019\)
- C \(2a + b = 2022\)
- D \(b \le 2020\)
Đáp án: A
Phương pháp giải:
- Lấy nguyên hàm hai vế từ đẳng thức đạo hàm và kết hợp điều kiện tìm \(f\left( x \right)\).
- Tính các giá trị \(f\left( 1 \right),f\left( 2 \right),...,f\left( {2019} \right)\) thay vào tính tổng.
- Tìm \(a,b\) và kết luận.
Lời giải chi tiết:
Ta có: \(f'\left( x \right) = \left( {2x + 1} \right){f^2}\left( x \right) \Leftrightarrow \frac{{f'\left( x \right)}}{{{f^2}\left( x \right)}} = 2x + 1\)
Nguyên hàm hai vế ta được:
\(\int {\frac{{f'\left( x \right)}}{{{f^2}\left( x \right)}}dx} = \int {\left( {2x + 1} \right)dx} \) \( \Rightarrow - \frac{1}{{f\left( x \right)}} = {x^2} + x + C\).
Do \(f\left( 1 \right) = - \frac{1}{2}\) nên \( - \frac{1}{{ - \frac{1}{2}}} = {1^2} + 1 + C \Leftrightarrow C = 0\).
Do đó \( - \frac{1}{{f\left( x \right)}} = {x^2} + x \Rightarrow f\left( x \right) = - \frac{1}{{{x^2} + x}} = \frac{1}{{x + 1}} - \frac{1}{x}\).
\( \Rightarrow f\left( 1 \right) + f\left( 2 \right) + ... + f\left( {2019} \right) = \frac{1}{2} - \frac{1}{1} + \frac{1}{3} - \frac{1}{2} + ... + \frac{1}{{2020}} - \frac{1}{{2019}} = \frac{1}{{2010}} - 1\).
Vậy \(a = 1,b = 2020\).
Đối chiếu các đáp án ta thấy A sai.
Chọn A.
>> 2K8 Chú ý! Lộ Trình Sun 2026 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi 26+ TN THPT, 90+ ĐGNL HN, 900+ ĐGNL HCM, 70+ ĐGTD - Click xem ngay) tại Tuyensinh247.com.Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, luyện thi theo 3 giai đoạn: Nền tảng lớp 12, Luyện thi chuyên sâu, Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục









