10 bài tập tổng hợp về Hình vuông
Làm đề thiCâu hỏi 1 :
Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau
- A Hình vuông
- B Hình thang cân
- C Hình chữ nhật
- D Hình thoi
Đáp án: D
Phương pháp giải:
Phương pháp: Dựa vào tính chất của hình vuông, hình thang cân, hình chữ nhật, hình thoi
Lời giải chi tiết:
Cách giải: Trong các hình: hình vuông, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai đường chéo không bằng nhau
Chọn D.
Câu hỏi 2 :
Hình thoi có một góc vuông là hình:
- A Hình thang vuông
- B Hình chữ nhật
- C Hình vuông
- D Hình bình hành
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng dấu hiệu nhận biết: Hình thoi có một góc vuông là hình vuông.
Lời giải chi tiết:
Cách giải: Theo dấu hiệu nhận biết: Hình thoi có một góc vuông là hình vuông.
Chọn C.
Câu hỏi 3 :
Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?
- A Hình bình hành
- B Hình chữ nhật
- C Hình vuông
- D Hình thang cân
Đáp án: C
Phương pháp giải:
Phương pháp: Dựa vào tính chất của hình vuông, hình bình hành, hình chữ nhật, hình thang cân
Lời giải chi tiết:
Cách giải: Hình vuông có hai đường chéo vuông góc với nhau.
Chọn C.
Câu hỏi 4 :
Cho đường chéo của cạnh hình vuông dài 5 cm, bình phương độ dài cạnh hình vuông là:
- A 25 cm
- B 20 cm
- C 12,5 cm
- D 20 cm
Đáp án: C
Phương pháp giải:
Phương pháp: Sử dụng định lí Py-ta-go trong tam giác vuông
Lời giải chi tiết:
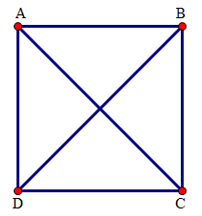
Cách giải: Có hình vuông ABCD( hình vẽ), AC là đường chéo
Xét tam giác ADC có \(\widehat{D}=90{}^\circ \)
\(\begin{align} & A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}} \\ & A{{C}^{2}}=2A{{D}^{2}}\,\,\,\,\,(do\,\,\,AD=DC) \\ & {{5}^{2}}=2A{{D}^{2}} \\ & \Rightarrow A{{D}^{2}}=12,5 \\\end{align}\)
Chọn C
Câu hỏi 5 :
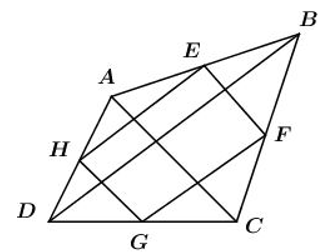
Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.
- A \(BD\bot AC;BD=AC\)
- B \(BD\bot AC\)
- C \(BD=AC\)
- D Tất cả các đáp án trên đều sai
Đáp án: A
Phương pháp giải:
Phương pháp: Dựa vào hai dấu hiệu nhận biết:
+ Hình bình hành có một góc vuông là hình chữ nhật
+ Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
Lời giải chi tiết:
Cách giải:
Hình bình hành EFGH là hình vuông khi và chỉ khi\(\left\{ \begin{align} & EH\bot EF \\ & EH=EF \\\end{align} \right.\)
Mà
\(\left\{ \begin{array}{l}EH//BD;\,\,\,EF//AC\\EH = \frac{1}{2}BD;\,\,EF = \frac{1}{2}AC\end{array} \right. \Rightarrow \left\{ \begin{array}{l}EH \bot EF\\EH = EF\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}BD \bot AC\\DB = AC\end{array} \right..\)
Chọn A
Câu hỏi 6 :
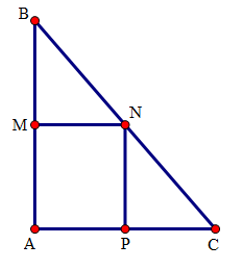
Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC. Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
- A \(AB=\frac{1}{2}AC\)
- B \(AB=AC\)
- C \(AC=\frac{1}{2}AB\)
- D \(\widehat{B}=60{}^\circ \)
Đáp án: B
Phương pháp giải:
Phương pháp:
Sử dụng dấu hiệu nhận biết:
+) Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông
Lời giải chi tiết:
Cách giải: Hình chữ nhật AMNP là hình vuông \(\Leftrightarrow AM=AP\) .
Mà \(AM=\frac{1}{2}AB;AP=\frac{1}{2}AC(gt)\) nên \(AM=AP\Leftrightarrow AB=AC\).
Vậy nếu tam giác ABC vuông cân tại A thì hình chữ nhật AMNP là hình vuông.
Chọn B.
Câu hỏi 7 :
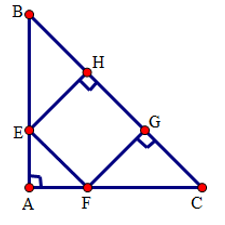
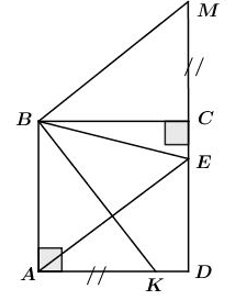
Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho \(BH=HG=GC\) . Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F.
a) Tứ giác EFGH là hình gì?
b) Cho \(BC=9cm\) . Tính độ dài các cạnh của tức giác EFGH.
Phương pháp giải:
Phương pháp:
+ Chứng minh tứ giác EFGH là hình bình hành thông qua dấu hiệu nhận biết: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành.
+ Chứng minh tứ giác EFGH là hình chữ nhật thông qua dấu hiệu nhận biết: Hình bình hành có một góc vuông là hình chữ nhật.
+ Chứng minh tứ giác EFGH là hình vuông thông qua dấu hiệu nhận biết: Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Lời giải chi tiết:
a) Ta có: \(\Delta ABC\) vuông cân tại A nên \(\widehat{B}=\widehat{C}=\frac{180{}^\circ -\widehat{A}}{2}=\frac{180{}^\circ -90{}^\circ }{2}=45{}^\circ \) .
Xét tam giác vuông FGC có
\(\begin{align} & \widehat{GFC}=180{}^\circ -\widehat{FGC}-\widehat{C}=180{}^\circ -90{}^\circ -45{}^\circ =45{}^\circ \\ & \Rightarrow \widehat{GFC}=\widehat{C} \\ \end{align}\)
Suy ra \(\Delta FGC\) là tam giác vuông cân tại G\(\Rightarrow FG=GC\) .
Chứng minh tương tự:
Xét tam giác vuông EHB có
\(\begin{align} & \widehat{BEH}=180{}^\circ -\widehat{EHB}-\widehat{B}=180{}^\circ -90{}^\circ -45{}^\circ =45{}^\circ \\ & \Rightarrow \widehat{BEH}=\widehat{B} \\ \end{align}\)
Suy ra tam giác EBH vuông cân tại H \(\Rightarrow EH=HB\) .
Mà \(BH=HG=GC(gt)\) nên \(FG=EH=HG\) .
Lại có: \(\left. \begin{align} & EH\bot BC(gt) \\ & FG\bot BC(gt) \\ \end{align} \right\}\Rightarrow EH\parallel FG\) ( định lí từ vuông góc đến song song)
Xét tứ giác EFGH có:
\(\begin{align} & EH=FG(cmt) \\ & EH\parallel FG(cmt) \\ \end{align}\)
\(\Rightarrow \) Tứ giác EFGH là hình bình hành(dhnb)
Mà \(\widehat{H}=90{}^\circ \) ( do \(EH\bot BC\) ) nên hình bình hành EFGH là hình chữ nhật.
Mặt khác \(EH=HG(cmt)\) nên hình chữ nhật EFGH là hình vuông.
b) Ta có: \(HG=\frac{BC}{3}=\frac{9}{3}=3cm\)
Do đó độ dài cạnh hình vuông EFGH là 3cm.
Câu hỏi 8 :
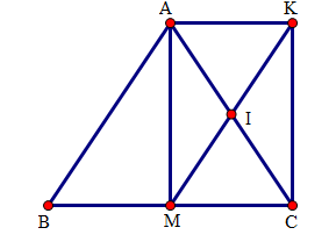
Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC. K là điểm đối xứng với M qua điểm I.
a) Chứng minh tứ giác AMCK là hình chữ nhật
b) Tứ giác AKMB là hình gì? Vì sao?
c) Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
Phương pháp giải:
Phương pháp:
a) Sử dụng dấu hiệu nhận biết:
+ Tứ giác có hai đường chéo cắt nhau tại trung điểm của mỗi đường là hình bình hành ,ta chứng minh được AMCK là hình bình hành.
+ Hình bình hành có một góc vuông là hình chữ nhật, ta chứng minh được hình bình hành AMCK là hình chữ nhật
b) Sử dụng dấu hiệu nhận biết: Tứ giác có hai cạnh đối song song và bằng nhau là hình bình hành .Ta chứng minh được tứ giác AKMB là hình bình hành
c) Sử dụng dấu hiệu nhận biết hình chữ nhật có hai cạnh kề bằng nhau là hình vuông để tìm ra điều kiện tam giác ABC vuông cân.
Lời giải chi tiết:
a) Tam giác ABC cân tại A, AM là đường trung tuyến nên AM đồng thời là đường cao
\(\Rightarrow AM\bot BC\Rightarrow \widehat{AMC}=90{}^\circ \)
Xét tứ giác AMCK có:
\(\begin{align} & AI=IC(gt) \\ & MI=IK(gt) \\ & AC\cap MK=I(gt) \\\end{align}\)
Suy ra tứ giác AMCK là hình bình hành (dhnb).
Lại có: \(\widehat{AMC}=90{}^\circ (cmt)\) nên hình bình hành AMCK là hình chữ nhật.
b) Ta có:
\(AK\parallel MC\) ( do AMCK là hình chữ nhật), \(M\in BC(gt)\Rightarrow AK\parallel BM\)
Mà \(BM=MC\) ( do AM là trung tuyến), \(AK=MC\) (do AMCK là hình chữ nhật) nên \(AK=BM\) (tính chất bắc cầu)
Xét tứ giác ABMK có:
\(\begin{align} & AK=BM(cmt) \\ & AK\parallel BM(cmt) \\\end{align}\)
Suy ra tứ giác ABMK là hình bình hành.
c) Hình chữ nhật AMCK là hình vuông \(\Leftrightarrow AM=MC\)
Mà \(MC=\frac{1}{2}BC(gt)\) nên \(AM=MC\Leftrightarrow AM=\frac{1}{2}BC\)
Do AM là đường trung tuyến của tam giác ABC nên \(AM=\frac{1}{2}BC\Leftrightarrow \) tam giác ABC vuông tại A.
Vậy nếu tam giác ABC vuông cân tại A thì tứ giác AMCK là hình vuông.
Câu hỏi 9 :
Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh rằng \(AK+CE=BE\) .
Phương pháp giải:
Phương pháp: Vẽ thêm điểm M trên tia đối của tia CD sao cho \(CM=AK\) . Từ đó \(AK+CE=CM+CE=EM\) . Bài toán đưa về việc chứng minh \(EM=BE\)
Lời giải chi tiết:
Cách giải:
Trên tia đối của tia CD lấy điểm M sao cho \(CM=AK\) . Ta có: \(AK+CE=CM+CE=EM\).
Ta cần chứng minh \(EM=BE\) .
Xét \(\Delta BAK\) và \(\Delta BCM\) có:
\(AK=CM\) ( cách vẽ)
\(\begin{align} & \widehat{A}=\widehat{C}=90{}^\circ (gt) \\ & BA=BC(gt) \\ & \Rightarrow \Delta BAK=\Delta BCM(c.g.c) \\ \end{align}\)
\(\Rightarrow \widehat{ABK}=\widehat{CBM};\widehat{\,\,AKB}=\widehat{CMB}\) ( góc tương ứng)
Mà \(\widehat{ABK}=\widehat{KBE}\) (gt) nên \(\widehat{KBE}=\widehat{CBM}\) (bắc cầu).
Ta có:
\(\widehat{EBM}=\widehat{EBC}+\widehat{CBM}=\widehat{EBC}+\widehat{KBE}=\widehat{KBC}=\widehat{AKB}(slt)=\widehat{CMB}\)
Suy ra tam giác EBM cân tại E (định nghĩa tam giác cân).
\(\begin{align} & \Rightarrow BE=EM \\ & \Rightarrow AK+CE=CM+CE=EM=BE \\ & \Rightarrow AK+CE=BE\,\,\,\,\left( dpcm \right). \\ \end{align}\)
Câu hỏi 10 :
Xét hai mênh đề:
(I): Tam giác ABC cân khi và chỉ khi nó có hai góc bằng nhau.
(II): Tứ giác ABCD là hình vuông khi và chỉ khi nó có 4 cạnh bằng nhau.
Khẳng định nào sau đây đúng?
- A Cả (I) và (II) đúng
- B (I) đúng và (II) sai
- C Cả (I) và (II) sai
- D (II) đúng và (I) sai
Đáp án: B
Phương pháp giải:
Sử dụng dấu hiệu nhận biết tam giác cân và hình vuông.
Lời giải chi tiết:
Tam giác ABC cân khi và chỉ khi nó có hai góc bằng nhau đúng \( \Rightarrow \left( I \right)\) đúng.
Tứ giác có 4 cạnh bằng nhau là hình thoi \( \Rightarrow \) (II) sai
Chọn B.
>> Học trực tuyến lớp 8 trên Tuyensinh247.com. Đầy đủ khoá học các bộ sách: Kết nối tri thức với cuộc sống; Chân trời sáng tạo; Cánh diều. Cam kết giúp học sinh lớp 8 học tốt, hoàn trả học phí nếu học không hiệu quả. PH/HS tham khảo chi tiết khoá học tại: Link
 |
 |
 |
 |
 |
 |
- 15 bài tập tổng hợp Ôn tập chương 2: Phân thức đại số
- 15 bài tập tổng hợp Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức
- 10 bài tập tổng hợp Phép nhân và phép chia các phân thức đại số
- 10 bài tập tổng hợp Phép cộng và phép trừ các phân thức đại số
- 10 bài tập tổng hợp Qui đồng mẫu thức nhiều phân thức