-
Đề kiểm tra 15 phút
-
Đề kiểm tra 15 phút – Chương 1 – Đại số và Giải tích 11
-
Đề kiểm tra 15 phút – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút – Chương 3 – Đại số và giải tích 11
-
Đề kiểm tra 15 phút - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 15 phút - Chương 1 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 2 - Hình học 11
-
Đề kiểm tra 15 phút - Chương 3 - Hình học 11
-
-
Đề kiểm tra 1 tiết
-
Đề kiểm tra 45 phút (1 tiết) – Chương 1 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) – Chương 2 – Đại số và giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 4 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút (1 tiết ) - Chương 5 - Đại số và Giải tích 11
-
Đề kiểm tra 45 phút ( 1 tiết) - Chương 1 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 2 - Hình học 11
-
Đề kiểm tra 45 phút (1 tiết) - Chương 3 - Hình học 11
-
-
Đề thi giữa kì 1
-
Đề thi học kì 1
-
Đề thi giữa kì 2
-
Đề thi học kì 2
Đề kiểm tra 1 tiết Toán 11 chương 4: Giới hạn - Đề số 1
Đề bài
Giá trị \(\lim \left( {{n^3} - 2n + 1} \right)\) bằng
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - \infty \)
-
D.
\( + \infty \)
Cho hàm số \(f\left( x \right) =\) \( \left\{ \begin{array}{l}\dfrac{{\tan x}}{x}\,\,\,khi\,\,x \ne 0,x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\\0\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng nào sau đây?
-
A.
\(\left( {0;\dfrac{\pi }{2}} \right)\)
-
B.
\(\left( { - \infty ;\dfrac{\pi }{4}} \right)\)
-
C.
\(\left( { - \dfrac{\pi }{4};\dfrac{\pi }{4}} \right)\)
-
D.
$R$
Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{x - \sqrt {x + 2} }}{{\sqrt {4x + 1} - 3}}$ bằng?
-
A.
$\dfrac{1}{2}.$
-
B.
$\dfrac{9}{8}.$
-
C.
$1.$
-
D.
$\dfrac{3}{4}.$
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{3 - \sqrt {9 - x} }}{x}\,\,\,khi\,\,0 < x < 9\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\\\dfrac{3}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 9\end{array} \right.\). Tìm \(m\) để \(f\left( x \right)\) liên tục trên \(\left[ {0; + \infty } \right)\).
-
A.
\(\dfrac{1}{3}\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{1}{6}\)
-
D.
$1$
Hàm số \(y = f\left( x \right)\) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
-
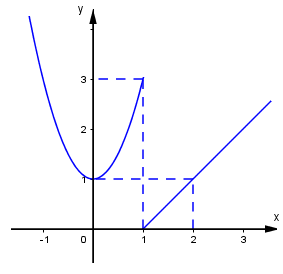
A.
$0$
-
B.
$1$
-
C.
$2$
-
D.
$3$
Giới hạn $\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)$ bằng?
-
A.
$0.$
-
B.
$ - \dfrac{1}{2}.$
-
C.
$ - \dfrac{1}{{\sqrt 2 }}.$
-
D.
$\dfrac{1}{{\sqrt 2 }}.$
Tính $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
-
A.
$5$
-
B.
$7$
-
C.
$9$
-
D.
$6$
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \sqrt[3]{{x + 1}}}}{{3x}}$ bằng?
-
A.
$ - \dfrac{1}{3}.$
-
B.
$0$.
-
C.
$\dfrac{1}{3}.$
-
D.
$\dfrac{{ - 1}}{9}.$
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - x\cos x\,\,\,khi\,\,x < 0\\\dfrac{{{x^2}}}{{1 + x}}\,\,\,\,\,\,\,\,\,\,khi\,\,0 \le x < 1\\{x^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\end{array} \right.\)
-
A.
Liên tục tại mọi điểm trừ điểm $x = 0.$
-
B.
Liên tục tại mọi điểm trừ $x = 1.$
-
C.
Liên tục tại mọi điểm trừ hai điểm $x = 0$ và $x = 1.$
-
D.
Liên tục tại mọi điểm \(x \in R\).
Tính $\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} - 3x - 8} \right)$ bằng?
-
A.
\(-2\)
-
B.
\(5\)
-
C.
\(9\)
-
D.
\(10\)
Chọn mệnh đề sai:
-
A.
\(\lim n = + \infty \)
-
B.
\(\lim \sqrt n = + \infty \)
-
C.
\(\lim \sqrt[3]{n} = + \infty \)
-
D.
\(\lim \dfrac{1}{n} = + \infty \)
Cho $n\in N^*$, nếu \(\left| q \right| < 1\) thì:
-
A.
\(\lim {q^n} = 0\)
-
B.
\(\lim q = 0\)
-
C.
\(\lim \left( {n.q} \right) = 0\)
-
D.
\(\lim \dfrac{n}{q} = 0\)
Dãy số nào dưới đây không có giới hạn \(0\)?
-
A.
\({u_n} = \dfrac{1}{{\sqrt n }}\)
-
B.
\({u_n} = \dfrac{1}{{\sqrt[3]{n}}}\)
-
C.
\({u_n} = \dfrac{{\sqrt[3]{n}}}{2}\)
-
D.
\({u_n} = 0\)
Trong các giới hạn sau giới hạn nào bằng $-1$?
-
A.
$\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^3} - 4}}.$
-
B.
$\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^2} - 1}}.$
-
C.
$\lim \dfrac{{2{n^2} - 3}}{{2{n^2} + 1}}.$
-
D.
$\lim \dfrac{{2{n^3} - 3}}{{2{n^2} - 1}}.$
Giới hạn $\lim \dfrac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}$bằng?
-
A.
$\dfrac{5}{2}.$
-
B.
$\dfrac{{ - 5}}{2}.$
-
C.
$1.$
-
D.
$ - 1.$
Cho dãy số $({u_n})$ với ${u_n} = \dfrac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}$. Khi đó $\lim {u_n}$ bằng?
-
A.
$ - \infty .$
-
B.
$ - 1.$
-
C.
$ + \infty .$
-
D.
$\dfrac{{ - 2}}{5}.$
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
-
A.
$-1$
-
B.
$0$
-
C.
$\dfrac{1}{2}.$
-
D.
$1$
Tính$\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} $ bằng?
-
A.
$ - \dfrac{{\sqrt 2 }}{2}$.
-
B.
$\dfrac{{\sqrt 2 }}{2}.$
-
C.
$\dfrac{1}{2}.$
-
D.
$ - \dfrac{1}{2}.$
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 3} - x} \right)$ bằng?
-
A.
$-1.$
-
B.
$0.$
-
C.
$\dfrac{1}{2}.$
-
D.
$1$
Cho $a$ và $b$ là các số thực khác $0.$ Tìm hệ thức liên hệ giữa $a$ và $b$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {ax + 1} - 1}}{x}\,\,\,khi\,\,x \ne 0\\4{x^2} + 5b\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) liên tục tại $x = 0.$
-
A.
$a = 5b$
-
B.
$a = 10b$
-
C.
$a = b$
-
D.
$a = 2b.$
Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?
-
A.
Nếu hàm số \(f\left( x \right)\) liên tục trên đoạn $[a; b]$ và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không có nghiệm trong khoảng \(\left( {a;b} \right)\).
-
B.
Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong khoảng \(\left( {a;b} \right)\).
-
C.
Nếu phương trình \(f\left( x \right) = 0\) có nghiệm trong khoảng \(\left( {a;b} \right)\) thì hàm số \(y = f\left( x \right)\) liên tục trên khoảng \(\left( {a;b} \right)\)
-
D.
Nếu hàm số \(y = f\left( x \right)\) liên tục tăng trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không thể có nghiệm trong \(\left( {a;b} \right)\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt {2x - 4} + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 2\\\dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2}}\,\,khi\,\,x < 2\end{array} \right.\)
Tìm tất cả các giá trị của tham số $m$ để hàm số liên tục trên $R.$
-
A.
$m = 3$
-
B.
$m = 4$
-
C.
$m = 5$
-
D.
$m = 6$
Cho dãy số $({u_n})$xác định bởi $\left\{ \begin{array}{ccccc}u _{1} = 1\\{u_{n + 1}} = \sqrt {{u_n}\left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)\left( {{u_n} + 3} \right) + 1} ,\,\,\left( {n \ge 1} \right)\end{array} \right.\,\,$. Đặt ${v_n} = \sum\limits_{i = 1}^n {\dfrac{1}{{{u_i} + 2}}} $. Tính $\lim {v_n}$bằng?
-
A.
$ + \infty .$
-
B.
$0.$
-
C.
$\dfrac{1}{2}.$
-
D.
$1.$
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[n]{{(x + 1)(x + 2)...(x + n)}} - x} \right)$ bằng:
-
A.
$0$
-
B.
$\dfrac{{n + 1}}{2}$
-
C.
$n$
-
D.
$1$
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 6} - a}}{{\sqrt {x + 1} - 2}}\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ne 3\\{x^3} - \left( {2b + 1} \right)x\,\,\,\,khi\,\,x = 3\end{array} \right.\) trong đó $a, b$ là các tham số thực. Biết hàm số liên tục tại $x = 3$. Số nhỏ hơn trong hai số $a$ và $b$ là:
-
A.
$2$
-
B.
$3$
-
C.
$4$
-
D.
$5$
Lời giải và đáp án
Giá trị \(\lim \left( {{n^3} - 2n + 1} \right)\) bằng
-
A.
\(0\)
-
B.
\(1\)
-
C.
\( - \infty \)
-
D.
\( + \infty \)
Đáp án : D
Đặt \({n^3}\) làm nhân tử chung và tính giới hạn.
Ta có: \({n^3} - 2n + 1 = {n^3}\left( {1 - \dfrac{2}{{{n^2}}} + \dfrac{1}{{{n^3}}}} \right)\).
Vì \(\lim {n^3} = + \infty \) và \(\lim \left( {1 - \dfrac{2}{{{n^2}}} + \dfrac{1}{{{n^3}}}} \right) = 1 > 0\) nên \(\lim \left( {{n^3} - 2n + 1} \right) = + \infty \)
Cho hàm số \(f\left( x \right) =\) \( \left\{ \begin{array}{l}\dfrac{{\tan x}}{x}\,\,\,khi\,\,x \ne 0,x \ne \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right)\\0\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\). Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng nào sau đây?
-
A.
\(\left( {0;\dfrac{\pi }{2}} \right)\)
-
B.
\(\left( { - \infty ;\dfrac{\pi }{4}} \right)\)
-
C.
\(\left( { - \dfrac{\pi }{4};\dfrac{\pi }{4}} \right)\)
-
D.
$R$
Đáp án : A
Xét tính liên tục của hàm số tại $x = 0,$ sử dụng giới hạn \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1\) .
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\tan x}}{x} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}.\dfrac{1}{{\cos x}} = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x}.\mathop {\lim }\limits_{x \to 0} \dfrac{1}{{\cos x}} = 1.\dfrac{1}{1} = 1\\f\left( 0 \right) = 0\end{array} \right\} \\ \Rightarrow \mathop {\lim }\limits_{x \to 0} f\left( x \right) \ne f\left( 0 \right)\)
\( \Rightarrow \) hàm số gián đoạn tại điểm $x = 0,$ do đó loại các đáp án B, C, D.
Tính $\mathop {\lim }\limits_{x \to 2} \dfrac{{x - \sqrt {x + 2} }}{{\sqrt {4x + 1} - 3}}$ bằng?
-
A.
$\dfrac{1}{2}.$
-
B.
$\dfrac{9}{8}.$
-
C.
$1.$
-
D.
$\dfrac{3}{4}.$
Đáp án : B
- Nhân liên hợp để khử dạng $\dfrac{0}{0}$.
$\begin{array}{l}\mathop {\lim }\limits_{x \to 2} \dfrac{{x - \sqrt {x + 2} }}{{\sqrt {4x + 1} - 3}} \\= \mathop {\lim }\limits_{x \to 2} \dfrac{{(x - \sqrt {x + 2} )(x + \sqrt {x + 2} )(\sqrt {4x + 1} + 3)}}{{(\sqrt {4x + 1} - 3)(\sqrt {4x + 1} + 3)(x + \sqrt {x + 2} )}} \\= \mathop {\lim }\limits_{x \to 2} \dfrac{{({x^2} - x - 2)(\sqrt {4x + 1} + 3)}}{{(4x + 1 - 9)(x + \sqrt {x + 2} )}}\\ = \mathop {\lim }\limits_{x \to 2} \dfrac{{(x + 1)(x - 2)(\sqrt {4x + 1} + 3)}}{{4(x - 2)(x + \sqrt {x + 2} )}} \\= \mathop {\lim }\limits_{x \to 2} \dfrac{{(x + 1)(\sqrt {4x + 1} + 3)}}{{4(x + \sqrt {x + 2} )}} \\= \dfrac{{(2 + 1)(\sqrt {4.2 + 1} + 3)}}{{4(2 + \sqrt {2 + 2} )}} = \dfrac{9}{8}\end{array}$
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{3 - \sqrt {9 - x} }}{x}\,\,\,khi\,\,0 < x < 9\\m\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x = 0\\\dfrac{3}{x}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 9\end{array} \right.\). Tìm \(m\) để \(f\left( x \right)\) liên tục trên \(\left[ {0; + \infty } \right)\).
-
A.
\(\dfrac{1}{3}\)
-
B.
\(\dfrac{1}{2}\)
-
C.
\(\dfrac{1}{6}\)
-
D.
$1$
Đáp án : C
Sử dụng lý thuyết:
- Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
- Hàm số \(y = f\left( x \right)\) liên tục trên nửa khoảng \(\left[ {a; + \infty } \right)\) nếu nó liên tục trên \(\left( {a; + \infty } \right)\) và \(\mathop {\lim }\limits_{x \to {a^ + }} f\left( x \right) = f\left( a \right)\).
Do đó ta chỉ cần xét tính liên tục của hàm số tại $x = 0$ và $x = 9.$
Hàm số liên tục trên \(\left( {0;9} \right) \cup \left( {9; + \infty } \right)\), ta cần xét tính liên tục của hàm số tại $x = 0$ và $x = 9.$
$\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{3 - \sqrt {9 - x} }}{x} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{9 - \left( {9 - x} \right)}}{{x\left( {3 + \sqrt {9 - x} } \right)}} = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{1}{{3 + \sqrt {9 - x} }} = \dfrac{1}{6}$
Mà $f\left( 0 \right) = m$ $\Rightarrow $ để hàm số liên tục tại $x = 0$ thì \(\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \dfrac{1}{6} = m\).
$\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {9^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ + }} \dfrac{3}{x} = \dfrac{1}{3}\\\mathop {\lim }\limits_{x \to {9^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ - }} \dfrac{{3 - \sqrt {9 - x} }}{x} = \dfrac{{3 - 0}}{9} = \dfrac{1}{3}\\f\left( 9 \right) = \dfrac{3}{9} = \dfrac{1}{3}\end{array} \right\} $
$ \Rightarrow \mathop {\lim }\limits_{x \to {9^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {9^ - }} f\left( x \right) = f\left( 9 \right) $ $\Rightarrow $ hàm số liên tục tại $x = 9.$
Vậy với \(m = \dfrac{1}{6}\) thì hàm số liên tục trên \(\left[ {0; + \infty } \right)\)
Hàm số \(y = f\left( x \right)\) có đồ thị dưới đây gián đoạn tại điểm có hoành độ bằng bao nhiêu?
-
A.
$0$
-
B.
$1$
-
C.
$2$
-
D.
$3$
Đáp án : B
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Quan sát đồ thị ta thấy \(\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = 3;\,\,\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = 0 \) \(\Rightarrow \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right)\) nên không tồn tại \(\mathop {\lim }\limits_{x \to {1^{}}} f\left( x \right)\). Do đó hàm số gián đoạn tại điểm $x = 1.$
Giới hạn $\lim \left( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } \right)$ bằng?
-
A.
$0.$
-
B.
$ - \dfrac{1}{2}.$
-
C.
$ - \dfrac{1}{{\sqrt 2 }}.$
-
D.
$\dfrac{1}{{\sqrt 2 }}.$
Đáp án : B
- Nhân liên hợp,
- Chia cả tử mẫu của phân thức cho n.
$\begin{array}{l}\lim ( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} } ) \\ =\lim \frac{{( {\sqrt {{n^2} - n + 1} - \sqrt {{n^2} + 1} }) ( {\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} } )}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }}\\ = \lim \frac{{{n^2} - n + 1 - {n^2} - 1}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }} \\= \lim \frac{{ - n}}{{\sqrt {{n^2} - n + 1} + \sqrt {{n^2} + 1} }} \\= \lim \frac{{ - 1}}{{\sqrt {1 - \frac{1}{n} + \frac{1}{{{n^2}}}} + \sqrt {1 + \frac{1}{{{n^2}}}} }} \\= -\frac{{1}}{2}\end{array}$
Tính $\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right)$ bằng?
-
A.
$5$
-
B.
$7$
-
C.
$9$
-
D.
$6$
Đáp án : C
Hàm số \(y = f\left( x \right)\) xác định tại \(x = {x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} = f\left( {{x_0}} \right)\)
$\mathop {\lim }\limits_{x \to - 1} \left( {{x^2} - x + 7} \right) = {( - 1)^2} - ( - 1) + 7 = 9.$
Tính $\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \sqrt[3]{{x + 1}}}}{{3x}}$ bằng?
-
A.
$ - \dfrac{1}{3}.$
-
B.
$0$.
-
C.
$\dfrac{1}{3}.$
-
D.
$\dfrac{{ - 1}}{9}.$
Đáp án : D
- Nhân liên hợp để khử dạng $\dfrac{0}{0}$.
$\begin{array}{l}\mathop {\lim }\limits_{x \to 0} \dfrac{{1 - \sqrt[3]{{x + 1}}}}{{3x}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{(1 - \sqrt[3]{{x + 1}})\left( {1 + \sqrt[3]{{x + 1}} + {{\left( {\sqrt[3]{{x + 1}}} \right)}^2}} \right)}}{{3x\left( {1 + \sqrt[3]{{x + 1}} + {{\left( {\sqrt[3]{{x + 1}}} \right)}^2}} \right)}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{1 - (x + 1)}}{{3x\left( {1 + \sqrt[3]{{x + 1}} + {{\left( {\sqrt[3]{{x + 1}}} \right)}^2}} \right)}}\\ = \mathop {\lim }\limits_{x \to 0} \dfrac{{ - x}}{{3x\left( {1 + \sqrt[3]{{x + 1}} + {{\left( {\sqrt[3]{{x + 1}}} \right)}^2}} \right)}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{ - 1}}{{3\left( {1 + \sqrt[3]{{x + 1}} + {{\left( {\sqrt[3]{{x + 1}}} \right)}^2}} \right)}} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{ - 1}}{{3\left( {1 + \sqrt[3]{{0 + 1}} + {{\left( {\sqrt[3]{{0 + 1}}} \right)}^2}} \right)}} = \dfrac{{ - 1}}{9}\end{array}$
Hàm số \(f\left( x \right) = \left\{ \begin{array}{l} - x\cos x\,\,\,khi\,\,x < 0\\\dfrac{{{x^2}}}{{1 + x}}\,\,\,\,\,\,\,\,\,\,khi\,\,0 \le x < 1\\{x^3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 1\end{array} \right.\)
-
A.
Liên tục tại mọi điểm trừ điểm $x = 0.$
-
B.
Liên tục tại mọi điểm trừ $x = 1.$
-
C.
Liên tục tại mọi điểm trừ hai điểm $x = 0$ và $x = 1.$
-
D.
Liên tục tại mọi điểm \(x \in R\).
Đáp án : B
Xét tính liên tục của hàm số tại $x = 0$ và $x = 1$
Hàm số \(y = f\left( x \right)\) liên tục tại điểm \(x = {x_0}\) khi và chỉ khi \(\mathop {\lim }\limits_{x \to {x_0^+}} f\left( x \right) =\mathop {\lim }\limits_{x \to {x_0^-}} f\left( x \right) =f\left( {{x_0}} \right)\)
Tức là, ta cần tìm giới hạn trái, giới hạn phải và giá trị của hàm số tại mỗi điểm cần xét tính liên tục.
+ Nếu hai giới hạn đó bằng nhau và bằng giá trị hàm số tại điểm đó thì hàm số liên tục.
+ Nếu giới hạn trái không bằng giới hạn phải thì hàm số không liên tục tại điểm xét.
+ Nếu hai giới hạn bằng nhau nhưng không bằng giá trị thì hàm số cũng không liên tục tại điểm xét.
Hàm số \(y = f\left( x \right)\) liên tục trên các khoảng \(\left( { - \infty ;0} \right),\left( {0;1} \right),\left( {1; + \infty } \right)\) nên ta chỉ xét tính liên tục của \(y = f\left( x \right)\) tại các điểm \(x = 0,x = 1\).
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ + }} \dfrac{{{x^2}}}{{1 + x}} = 0\\\mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} \left( { - x\cos x} \right) = 0\\f\left( 0 \right) = \dfrac{0}{{1 + 0}} = 0\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {0^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {0^ - }} f\left( x \right) = f\left( 0 \right) \) \(\Rightarrow \) hàm số liên tục tại $x = 0.$
\(\left. \begin{array}{l}\mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ + }} {x^3} = 1\\\mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{{x^2}}}{{1 + x}} = \dfrac{1}{{1 + 1}} = \dfrac{1}{2}\end{array} \right\} \Rightarrow \mathop {\lim }\limits_{x \to {1^ + }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right) \Rightarrow \)Không tồn tại \(\mathop {\lim }\limits_{x \to 1} f\left( x \right)\) \( \Rightarrow \) hàm số không liên tục tại $x = 1.$
Vậy hàm số liên tục tại mọi điểm trừ $x = 1.$
Tính $\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} - 3x - 8} \right)$ bằng?
-
A.
\(-2\)
-
B.
\(5\)
-
C.
\(9\)
-
D.
\(10\)
Đáp án : D
Hàm số \(y = f\left( x \right)\) xác định tại \(x = {x_0}\) thì \(\mathop {\lim }\limits_{x \to {x_0}} = f\left( {{x_0}} \right)\)
$\mathop {\lim }\limits_{x \to - 2} \left( {3{x^2} - 3x - 8} \right) = 3.{( - 2)^2} - 3.( - 2) - 8 = 12 + 6 - 8 = 10.$
Chọn mệnh đề sai:
-
A.
\(\lim n = + \infty \)
-
B.
\(\lim \sqrt n = + \infty \)
-
C.
\(\lim \sqrt[3]{n} = + \infty \)
-
D.
\(\lim \dfrac{1}{n} = + \infty \)
Đáp án : D
Ta có: \(\lim n = + \infty ,\lim \sqrt n = + \infty ,\) \(\lim \sqrt[3]{n} = + \infty ,\) \(\lim \dfrac{1}{n} = 0 \)
Vậy chỉ có đáp án D là sai.
Cho $n\in N^*$, nếu \(\left| q \right| < 1\) thì:
-
A.
\(\lim {q^n} = 0\)
-
B.
\(\lim q = 0\)
-
C.
\(\lim \left( {n.q} \right) = 0\)
-
D.
\(\lim \dfrac{n}{q} = 0\)
Đáp án : A
Định lý: Nếu \(\left| q \right| < 1\) thì \(\lim {q^n} = 0\).
Dãy số nào dưới đây không có giới hạn \(0\)?
-
A.
\({u_n} = \dfrac{1}{{\sqrt n }}\)
-
B.
\({u_n} = \dfrac{1}{{\sqrt[3]{n}}}\)
-
C.
\({u_n} = \dfrac{{\sqrt[3]{n}}}{2}\)
-
D.
\({u_n} = 0\)
Đáp án : C
Các dãy số có giới hạn \(0\) là: \({u_n} = \dfrac{1}{{\sqrt n }},{u_n} = \dfrac{1}{{\sqrt[3]{n}}},{u_n} = 0\).
Dãy số \(\left( {{u_n}} \right)\) ở đáp án C có \(\lim {u_n} = \lim \dfrac{{\sqrt[3]{n}}}{2} = + \infty \)
Trong các giới hạn sau giới hạn nào bằng $-1$?
-
A.
$\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^3} - 4}}.$
-
B.
$\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^2} - 1}}.$
-
C.
$\lim \dfrac{{2{n^2} - 3}}{{2{n^2} + 1}}.$
-
D.
$\lim \dfrac{{2{n^3} - 3}}{{2{n^2} - 1}}.$
Đáp án : B
Chia cả tử mẫu của phân thức cho lũy thừa bậc cao nhất của tử và mẫu.
$\begin{array}{l}\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^3} - 4}} = \lim \dfrac{{\dfrac{2}{n} - \dfrac{3}{{{n^3}}}}}{{ - 2 - \dfrac{4}{{{n^3}}}}} = \dfrac{0}{{ - 2}} = 0.\\\lim \dfrac{{2{n^2} - 3}}{{ - 2{n^2} - 1}} = \lim \dfrac{{2 - \dfrac{3}{{{n^2}}}}}{{ - 2 - \dfrac{1}{{{n^2}}}}} = \dfrac{2}{{ - 2}} = - 1.\\\lim \dfrac{{2{n^2} - 3}}{{2{n^2} + 1}} = \lim \dfrac{{2 - \dfrac{3}{{{n^2}}}}}{{2 + \dfrac{1}{{{n^2}}}}} = \dfrac{2}{2} = 1.\\\lim \dfrac{{2{n^3} - 3}}{{2{n^2} - 1}} = \lim \dfrac{{2 - \dfrac{3}{{{n^3}}}}}{{\dfrac{2}{n} - \dfrac{1}{{{n^3}}}}} = + \infty .\end{array}$
Giới hạn $\lim \dfrac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}}$bằng?
-
A.
$\dfrac{5}{2}.$
-
B.
$\dfrac{{ - 5}}{2}.$
-
C.
$1.$
-
D.
$ - 1.$
Đáp án : D
- Nhân liên hợp,
- Chia cả tử mẫu của phân thức cho ${n^2}$.
Cách 1:
$\begin{array}{l}\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}} \\= \lim \frac{{( {\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} } ).( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} })}}{{( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} }).(2n - 1)}}\\ = \lim \frac{{({n^2} - 3n - 5) - (9{n^2} + 3)}}{{( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } ).(2n - 1)}} \\= \lim \frac{{ - 8{n^2} - 3n - 8}}{{( {\sqrt {{n^2} - 3n - 5} + \sqrt {9{n^2} + 3} } ).(2n - 1)}}\\ = \lim \frac{{ - 8 - \frac{3}{n} - \frac{8}{{{n^2}}}}}{{( {\sqrt {1 - \frac{3}{n} - \frac{5}{{{n^2}}}} + \sqrt {9 + \frac{3}{{{n^2}}}} })( {2 - \frac{1}{n}} )}} = \frac{{ - 8}}{{4.2}} = - 1.\end{array}$
Cách 2: Chia cả tử và mẫu cho $n.$
$\lim \frac{{\sqrt {{n^2} - 3n - 5} - \sqrt {9{n^2} + 3} }}{{2n - 1}} = \lim \frac{{\sqrt {1 - \frac{3}{n} - \frac{5}{{{n^2}}}} - \sqrt {9 + \frac{3}{{{n^2}}}} }}{{2 - \frac{1}{n}}} = \lim \frac{{1 - 3}}{2} = - 1$
Cho dãy số $({u_n})$ với ${u_n} = \dfrac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}$. Khi đó $\lim {u_n}$ bằng?
-
A.
$ - \infty .$
-
B.
$ - 1.$
-
C.
$ + \infty .$
-
D.
$\dfrac{{ - 2}}{5}.$
Đáp án : A
- Chia cả tử mẫu của phân thức cho ${n^2}$.
- Giới hạn $\lim {u_n} = L,\lim {v_n} = 0 \Rightarrow \lim \dfrac{{{u_n}}}{{{v_n}}} = \infty $
$\lim {u_n} = \lim \dfrac{{\left( {2n + 1} \right)\left( {1 - 3n} \right)}}{{\sqrt[3]{{{n^3} + 5n - 1}}}}$ $ = \lim \dfrac{{ - 6{n^2} - n + 1}}{{\sqrt[3]{{{n^3} + 5n - 1}}}} $ $= \lim \dfrac{{\dfrac{{ - 6{n^2} - n + 1}}{{{n^2}}}}}{{\sqrt[3]{{\dfrac{{{n^3} + 5n - 1}}{{{n^6}}}}}}}$ $=\lim \dfrac{{ - 6 - \dfrac{1}{n} + \dfrac{1}{{{n^2}}}}}{{\sqrt[3]{{\dfrac{1}{{{n^3}}} + \dfrac{5}{{{n^5}}} - \dfrac{1}{{{n^6}}}}}}} = - \infty .$
Tính $\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right)$ bằng?
-
A.
$-1$
-
B.
$0$
-
C.
$\dfrac{1}{2}.$
-
D.
$1$
Đáp án : A
- Nhân liên hợp để khử dạng $\infty - \infty $
- Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất.
- Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$.
$\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } \left( {\sqrt {{x^2} + 1} + x - 1} \right) \\ = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\left( {\sqrt {{x^2} + 1} + x - 1} \right)\left( {\sqrt {{x^2} + 1} - x + 1} \right)}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {{(x - 1)}^2}}}{{\sqrt {{x^2} + 1} - x + 1}}\\=\mathop {\lim }\limits_{x \to - \infty } \dfrac{{{x^2} + 1 - {x^2} + 2x - 1}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{2x}}{{\sqrt {{x^2} + 1} - x + 1}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{{\dfrac{{2x}}{x}}}{{\dfrac{{\sqrt {{x^2} + 1} }}{x} - \dfrac{x}{x} + \dfrac{1}{x}}} \\= \mathop {\lim }\limits_{x \to - \infty } \dfrac{2}{{ - \sqrt {1 + \dfrac{1}{{{x^2}}}} - 1 + \dfrac{1}{x}}}\\ = \dfrac{2}{{ - 1 - 1 + 0}} = - 1\end{array}$
Tính$\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} $ bằng?
-
A.
$ - \dfrac{{\sqrt 2 }}{2}$.
-
B.
$\dfrac{{\sqrt 2 }}{2}.$
-
C.
$\dfrac{1}{2}.$
-
D.
$ - \dfrac{1}{2}.$
Đáp án : A
- Đưa $x - 1$ vào trong căn: $x - 1 = - \sqrt {{{(x - 1)}^2}} \,\,\,\,khi\,\,x \to - \infty $
- Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất.
- Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$.
$\begin{array}{l}\mathop {\lim }\limits_{x \to - \infty } (x - 1)\sqrt {\dfrac{{{x^2}}}{{2{x^4} + {x^2} + 1}}} \\= \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^2}{{(x - 1)}^2}}}{{2{x^4} + {x^2} + 1}}} } \right] \\= \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^2}({x^2} - 2x + 1)}}{{2{x^4} + {x^2} + 1}}} } \right]\\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{{x^4} - 2{x^3} + {x^2}}}{{2{x^4} + {x^2} + 1}}} } \right]\\ = \mathop {\lim }\limits_{x \to - \infty } \left[ { - \sqrt {\dfrac{{1 - \dfrac{2}{x} + \dfrac{1}{{{x^2}}}}}{{2 + \dfrac{1}{{{x^2}}} + \dfrac{1}{{{x^4}}}}}} } \right] = - \dfrac{{\sqrt 2 }}{2}\end{array}$
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 3} - x} \right)$ bằng?
-
A.
$-1.$
-
B.
$0.$
-
C.
$\dfrac{1}{2}.$
-
D.
$1$
Đáp án : C
Bước 1: Nhân liên hợp để khử dạng $\infty - \infty $
Bước 2: Chia cả tử và mẫu cho lũy thừa của $x$ bậc cao nhất.
Bước 3: Thay giới hạn $\mathop {\lim }\limits_{x \to \infty } \dfrac{C}{{{x^n}}} = 0,\,\,\,n \in {\mathbb{N}^*}$.
Bước 1:
$\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt {{x^2} + x + 3} - x} \right) \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{\left( {\sqrt {{x^2} + x + 3} - x} \right)\left( {\sqrt {{x^2} + x + 3} + x} \right)}}{{\left( {\sqrt {{x^2} + x + 3} + x} \right)}} \\= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{{x^2} + x + 3 - {x^2}}}{{\sqrt {{x^2} + x + 3} + x}}\\ = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + 3}}{{\sqrt {{x^2} + x + 3} + x}} \end{array}$
Bước 2:
$= \mathop {\lim }\limits_{x \to + \infty } \dfrac{{1 + \dfrac{3}{x}}}{{\sqrt {1 + \dfrac{1}{x} + \dfrac{3}{{{x^2}}}} + 1}} $
Bước 3:
$= \dfrac{{1 + 0}}{{\sqrt {1 + 0 + 0} + 1}} = \dfrac{1}{2}$
Cho $a$ và $b$ là các số thực khác $0.$ Tìm hệ thức liên hệ giữa $a$ và $b$ để hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {ax + 1} - 1}}{x}\,\,\,khi\,\,x \ne 0\\4{x^2} + 5b\,\,\,\,\,\,\,\,\,khi\,\,x = 0\end{array} \right.\) liên tục tại $x = 0.$
-
A.
$a = 5b$
-
B.
$a = 10b$
-
C.
$a = b$
-
D.
$a = 2b.$
Đáp án : B
Bước 1: Tính \(\mathop {\lim }\limits_{x \to 0} f\left( x \right)\) và \(f\left( 0\right)\)
Bước 2: Để hàm số liên tục tại $x = 0$ thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right)\)
Bước 1:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 0} f\left( x \right) = \mathop {\lim }\limits_{x \to 0} \dfrac{{\sqrt {ax + 1} - 1}}{x} \\= \mathop {\lim }\limits_{x \to 0} \dfrac{{ax + 1 - 1}}{{x\left( {\sqrt {ax + 1} + 1} \right)}} = \mathop {\lim }\limits_{x \to 0} \dfrac{a}{{\sqrt {ax + 1} + 1}}\\ = \dfrac{a}{{\sqrt {a.0 + 1} + 1}} = \dfrac{a}{2}\\f\left( 0 \right) = 5b\end{array}\)
Bước 2:
Để hàm số liên tục tại $x = 0$ thì \(\mathop {\lim }\limits_{x \to 0} f\left( x \right) = f\left( 0 \right) \Leftrightarrow \dfrac{a}{2} = 5b \Leftrightarrow a = 10b\)
Cho hàm số \(f\left( x \right)\) xác định trên $[a; b].$ Trong các khẳng định sau, khẳng định nào đúng?
-
A.
Nếu hàm số \(f\left( x \right)\) liên tục trên đoạn $[a; b]$ và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không có nghiệm trong khoảng \(\left( {a;b} \right)\).
-
B.
Nếu \(f\left( a \right).f\left( b \right) < 0\) thì phương trình \(f\left( x \right) = 0\) có ít nhất một nghiệm trong khoảng \(\left( {a;b} \right)\).
-
C.
Nếu phương trình \(f\left( x \right) = 0\) có nghiệm trong khoảng \(\left( {a;b} \right)\) thì hàm số \(y = f\left( x \right)\) liên tục trên khoảng \(\left( {a;b} \right)\)
-
D.
Nếu hàm số \(y = f\left( x \right)\) liên tục tăng trên đoạn \(\left[ {a;b} \right]\) và \(f\left( a \right).f\left( b \right) > 0\) thì phương trình \(f\left( x \right) = 0\) không thể có nghiệm trong \(\left( {a;b} \right)\).
Đáp án : D
Nhận xét từng đáp án, sử dụng định lí: Nếu hàm số \(y = f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\) và \(f\left( a \right).f\left( b \right) < 0\) thì tồn tại ít nhất một số \({x_0} \in \left( {a;b} \right)\) sao cho \(f\left( {{x_0}} \right) = 0\).
Đáp án A sai. Chẳng hạn xét hàm số \(f\left( x \right) = {x^2} - 5.\) Hàm số này xác định trên \(\left[ { - 3;3} \right]\) và liên tục trên đoạn đó, đồng thời \(f\left( { - 3} \right).f\left( 3 \right) = 16 > 0\) nhưng phương trình \(f\left( x \right) = {x^2} - 5 = 0\) có nghiệm $x = \pm \sqrt 5 \in \left( { - 3;3} \right)$
Đáp án B sai vì thiếu điều kiện \(f\left( x \right)\) liên tục trên \(\left( {a;b} \right)\).
Đáp án C sai. Ví dụ xét hàm số \(f\left( x \right) = \left\{ \begin{array}{l}x + 1\,\,\,khi\,\,x < 0\\x + 2\,\,khi\,\,x \ge 0\end{array} \right.\). Hàm số này xác định trên \(\left[ { - 3;3} \right]\), có nghiệm \(x = - 1\) thuộc khoảng \(\left( { - 3;3} \right)\) nhưng gián đoạn tại điểm \(x = 0 \in \left( { - 3;3} \right)\) nên không liên tục trên khoảng \(\left( { - 3;3} \right)\) .
Đáp án D đúng. Thật vậy:
+ Vì hàm số \(y = f\left( x \right)\) liên tục tăng trên đoạn \(\left[ {a;b} \right]\) nên \(f\left( a \right) < f\left( x \right) < f\left( b \right)\,\,\forall x \in \left( {a;b} \right)\)
TH1: \(\left\{ \begin{array}{l}f\left( a \right) > 0\\f\left( b \right) > 0\\f\left( a \right) < f\left( x \right) < f\left( b \right)\end{array} \right. \Rightarrow f\left( x \right) > 0\)
TH2: \(\left\{ \begin{array}{l}f\left( a \right) < 0\\f\left( b \right) < 0\\f\left( a \right) < f\left( x \right) < f\left( b \right)\end{array} \right. \Rightarrow f\left( x \right) < 0\)
Vậy không có giá trị nào của $x$ để \(f\left( x \right) = 0\), hay phương trình \(f\left( x \right) = 0\) không thể có nghiệm trong \(\left( {a;b} \right)\).
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\sqrt {2x - 4} + 3\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ge 2\\\dfrac{{x + 1}}{{{x^2} - 2mx + 3m + 2}}\,\,khi\,\,x < 2\end{array} \right.\)
Tìm tất cả các giá trị của tham số $m$ để hàm số liên tục trên $R.$
-
A.
$m = 3$
-
B.
$m = 4$
-
C.
$m = 5$
-
D.
$m = 6$
Đáp án : C
- Sử dụng tính chất hàm phân thức hữu tỉ liên tục trên tập xác định của chúng.
- Xét tính liên tục của hàm số tại $x = 2:$ \(\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right)\)
Ta có hàm số liên tục trên \(\left( {2; + \infty } \right)\)
Ta có \(f\left( 2 \right) = \sqrt {2.2 - 4} + 3 = 3;\,\,\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( {\sqrt {2x - 4} + 3} \right) = 3\)
Hàm số liên tục trên \(\mathbb{R} \Leftrightarrow \) Hàm số liên tục trên \(\left( { - \infty ;2} \right)\) và liên tục tại \(x = 2\)
\( \Leftrightarrow \) Hàm số xác định trên \(\left( { - \infty ;2} \right)\) và liên tục tại \(x = 2\)
\( \Leftrightarrow \)\(\left\{ \begin{array}{l}{x^2} - 2mx + 3m + 2 \ne 0\forall x \in \left( { - \infty ;2} \right){\rm{ (1)}}\\\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = f\left( 2 \right){\rm{ (2)}}\end{array} \right.\)
\(\begin{array}{l}(2) \Leftrightarrow \mathop {\lim }\limits_{x \to {2^ - }} = 3 \Leftrightarrow \dfrac{{2 + 1}}{{{2^2} - 2m.2 + 3m + 2}} = 3\\ \Leftrightarrow \dfrac{3}{{6 - m}} = 3 \Leftrightarrow m = 5\end{array}\)
Thay \(m = 5\) vào \((1)\) ta được \({x^2} - 10x + 17 \ne 0\forall x \in \left( { - \infty ;2} \right)\).
Vậy với $m = 5$ thì hàm số liên tục trên \(\mathbb{R}\).
Cho dãy số $({u_n})$xác định bởi $\left\{ \begin{array}{ccccc}u _{1} = 1\\{u_{n + 1}} = \sqrt {{u_n}\left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)\left( {{u_n} + 3} \right) + 1} ,\,\,\left( {n \ge 1} \right)\end{array} \right.\,\,$. Đặt ${v_n} = \sum\limits_{i = 1}^n {\dfrac{1}{{{u_i} + 2}}} $. Tính $\lim {v_n}$bằng?
-
A.
$ + \infty .$
-
B.
$0.$
-
C.
$\dfrac{1}{2}.$
-
D.
$1.$
Đáp án : C
- Biến đổi, rút gọn biểu thức${v_n}$ rồi tính giới hạn.
${u_2} = \sqrt {1.2.3.4 + 1} = 5,$ ${u_n} > 0,\forall n = 1;2;...$
Ta có:
$\begin{array}{l}{u_{n + 1}} = \sqrt {{u_n}\left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)\left( {{u_n} + 3} \right) + 1} = \sqrt {\left( {u_n^2 + 3{u_n}} \right)\left( {u_n^2 + 3{u_n} + 2} \right) + 1} \\ = \sqrt {{{\left( {u_n^2 + 3{u_n}} \right)}^2} + 2\left( {u_n^2 + 3{u_n}} \right) + 1} = \sqrt {{{\left( {u_n^2 + 3{u_n} + 1} \right)}^2}} = u_n^2 + 3{u_n} + 1\\ \Rightarrow {u_{n + 1}} + 1 = u_n^2 + 3{u_n} + 2 = \left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)\\ \Rightarrow \dfrac{1}{{{u_{n + 1}} + 1}} = \dfrac{1}{{\left( {{u_n} + 1} \right)\left( {{u_n} + 2} \right)}} = \dfrac{1}{{{u_n} + 1}} - \dfrac{1}{{{u_n} + 2}}\\ \Rightarrow \dfrac{1}{{{u_n} + 2}} = \dfrac{1}{{{u_n} + 1}} - \dfrac{1}{{{u_{n + 1}} + 1}}\end{array}$
Do đó:
\({v_n} = \sum\limits_{i = 1}^n {\dfrac{1}{{{u_i} + 2}} = } \sum\limits_{i = 1}^n {\left( {\dfrac{1}{{{u_i} + 1}} - \dfrac{1}{{{u_{i + 1}} + 1}}} \right)}\) \( = \dfrac{1}{{{u_1} + 1}} - \dfrac{1}{{{u_{n + 1}} + 1}} = \dfrac{1}{2} - \dfrac{1}{{{u_{n + 1}} + 1}}\)
Xét hiệu \({u_{n + 1}} - {u_n} = u_n^2 + 3{u_n} + 1 - {u_n} = {\left( {{u_n} + 1} \right)^2} > 0\)
$ \Rightarrow \left( {{u_n}} \right)$ là dãy tăng.
Giả sử \(\lim {u_{n + 1}} = \lim {u_n} = a > 0 \Rightarrow a = {a^2} + 3a + 1 \Rightarrow {a^2} + 2a + 1 = 0 \Leftrightarrow a = - 1\,\,\left( {ktm} \right) \Rightarrow \lim {u_n} = + \infty \)
$ \Rightarrow \lim {v_n} = \dfrac{1}{2} - \dfrac{1}{{{u_{n + 1}} + 1}} = \dfrac{1}{2} - 0 = \dfrac{1}{2}.$
Tính $\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[n]{{(x + 1)(x + 2)...(x + n)}} - x} \right)$ bằng:
-
A.
$0$
-
B.
$\dfrac{{n + 1}}{2}$
-
C.
$n$
-
D.
$1$
Đáp án : B
- Đặt $x = \dfrac{1}{y}$, khi $x \to + \infty :\,\,\,y \to 0$ .
- Nhân liên hợp, tính $\mathop {\lim }\limits_{y \to 0} \dfrac{{\sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1}}{y}$.
Đặt $x = \dfrac{1}{y}$, khi $x \to + \infty :\,\,\,y \to 0$
$\mathop {\lim }\limits_{x \to + \infty } \left( {\sqrt[n]{{(x + 1)(x + 2)...(x + n)}} - x} \right) = \mathop {\lim }\limits_{y \to 0} \left( {\sqrt[n]{{\left( {\dfrac{1}{y} + 1} \right)\left( {\dfrac{1}{y} + 2} \right)...\left( {\dfrac{1}{y} + n} \right)}} - \dfrac{1}{y}} \right) = \mathop {\lim }\limits_{y \to 0} \dfrac{{\sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1}}{y}$
$\begin{array}{l}\sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1\\ = \sqrt[n]{{1 + y}} - \sqrt[n]{{1 + y}} + \sqrt[n]{{\left( {1 + y} \right)\left( {1 + 2y} \right)}} - \sqrt[n]{{\left( {1 + y} \right)\left( {1 + 2y} \right)}} + ... + \sqrt[n]{{(1 + y)(1 + 2y)...(1 + (n - 1)y)}}\\\,\,\,\,\, - \sqrt[n]{{(1 + y)(1 + 2y)...(1 + (n - 1)y)}} + \sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1\\ = \left( {\sqrt[n]{{1 + y}} - 1} \right) + \sqrt[n]{{1 + y}}\left( {\sqrt[n]{{1 + 2y}} - 1} \right) + ... + \sqrt[n]{{(1 + y)(1 + 2y)...(1 + (n - 1)y)}}\left( {\sqrt[n]{{1 + ny}} - 1} \right)\\ \Rightarrow \mathop {\lim }\limits_{y \to 0} \dfrac{{\sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1}}{y} = \mathop {\lim }\limits_{y \to 0} \left[ {\dfrac{{\left( {\sqrt[n]{{1 + y}} - 1} \right)}}{y}} \right] + \mathop {\lim }\limits_{y \to 0} \left[ {\sqrt[n]{{1 + y}}.\dfrac{{\left( {\sqrt[n]{{1 + 2y}} - 1} \right)}}{y}} \right] + ... + \\\,\,\,\,\,\mathop {\lim }\limits_{y \to 0} \left[ {\sqrt[n]{{(1 + y)(1 + 2y)...(1 + (n - 1)y)}}.\dfrac{{\left( {\sqrt[n]{{1 + ny}} - 1} \right)}}{y}} \right]\end{array}$
Tổng quát:
$\begin{array}{l}\mathop {\lim }\limits_{y \to 0} \left[ {\sqrt[n]{{(1 + y)(1 + 2y)...(1 + (k - 1)y)}}.\dfrac{{\sqrt[n]{{1 + ky}} - 1}}{y}} \right]\\ = \mathop {\lim }\limits_{y \to 0} \left[ {\sqrt[n]{{(1 + y)(1 + 2y)...(1 + (k - 1)y)}}.\dfrac{{\left( {\sqrt[n]{{1 + ky}} - 1} \right)\left[ {{{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 1}} + {{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 2}} + ... + 1} \right]}}{{y\left[ {{{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 1}} + {{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 2}} + ... + 1} \right]}}} \right]\\ = \mathop {\lim }\limits_{y \to 0} \dfrac{{(1 + ky - 1).\sqrt[n]{{(1 + y)(1 + 2y)...(1 + (k - 1)y)}}}}{{y{{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 1}} + {{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 2}} + ... + 1}}\\ = \mathop {\lim }\limits_{y \to 0} \dfrac{{k.\sqrt[n]{{(1 + y)(1 + 2y)...(1 + (k - 1)y)}}}}{{{{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 1}} + {{\left( {\sqrt[n]{{1 + ky}}} \right)}^{n - 2}} + ... + 1}} = \dfrac{k}{n}\end{array}$
Khi đó:
$\mathop {\lim }\limits_{y \to 0} \dfrac{{\sqrt[n]{{(1 + y)(1 + 2y)...(1 + ny)}} - 1}}{y} = \dfrac{1}{n} + \dfrac{2}{n} + \dfrac{3}{n} + ... + \dfrac{n}{n} = \dfrac{{1 + 2 + 3 + ... + n}}{n} = \dfrac{{\dfrac{{n(n + 1)}}{2}}}{n} = \dfrac{{n + 1}}{2}$
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}\dfrac{{\sqrt {x + 6} - a}}{{\sqrt {x + 1} - 2}}\,\,\,\,\,\,\,\,\,\,\,khi\,\,x \ne 3\\{x^3} - \left( {2b + 1} \right)x\,\,\,\,khi\,\,x = 3\end{array} \right.\) trong đó $a, b$ là các tham số thực. Biết hàm số liên tục tại $x = 3$. Số nhỏ hơn trong hai số $a$ và $b$ là:
-
A.
$2$
-
B.
$3$
-
C.
$4$
-
D.
$5$
Đáp án : B
Xét các trường hợp của $a$ và tính \(\mathop {\lim }\limits_{x \to 3} f\left( x \right)\) , để hàm số liên tục tại $x = 3$ thì \(\mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right)\)
\(f\left( 3 \right) = 27 - 3\left( {2b + 1} \right)\)
Đặt \(g\left( x \right) = \sqrt {x + 6} - a\).
Ta có \(g\left( 3 \right) = 3 - a\)
Nếu \(a = 3\) thì $\mathop {\lim }\limits_{x \to 3} f\left( x \right) = \mathop {\lim }\limits_{x \to 3} \dfrac{{\sqrt {x + 6} - 3}}{{\sqrt {x + 1} - 2}} = \mathop {\lim }\limits_{x \to 3} \dfrac{{\left( {x - 3} \right)\left( {\sqrt {x + 1} + 2} \right)}}{{\left( {x - 3} \right)\left( {\sqrt {x + 6} + 3} \right)}} = \dfrac{4}{6} = \dfrac{2}{3}$
Để hàm số liên tục tại $x = 3$ \( \Leftrightarrow \mathop {\lim }\limits_{x \to 3} f\left( x \right) = f\left( 3 \right) \Leftrightarrow 27 - 3\left( {2b + 1} \right) = \dfrac{2}{3} \Leftrightarrow b = \dfrac{{35}}{9}\)
Nếu \(a \ne 3 \Leftrightarrow g\left( 3 \right) \ne 0 \Rightarrow \mathop {\lim }\limits_{x \to 3} \dfrac{{g\left( x \right)}}{{\sqrt {x + 1} - 2}} = \infty \Rightarrow \)Hàm số không thể liên tục tại $x = 3.$
Vậy \(a = 3,b = \dfrac{{35}}{9}\)
>> Lộ Trình Sun 2025 - 3IN1 - 1 lộ trình ôn 3 kì thi (Luyện thi TN THPT & ĐGNL; ĐGTD) tại Tuyensinh247.com. Đầy đủ theo 3 đầu sách, Thầy Cô giáo giỏi, 3 bước chi tiết: Nền tảng lớp 12; Luyện thi chuyên sâu; Luyện đề đủ dạng đáp ứng mọi kì thi.
 |
 |
 |
 |
 |
 |
 |
 |
Các bài khác cùng chuyên mục
- Đề thi giữa kì 1 Toán 11 - Đề số 5
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 2
- Đề kiểm tra 15 phút Toán 11 chương 7: Quan hệ song song trong không gian - Đề số 3
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 1
- Đề kiểm tra 15 phút Toán 11 chương 8: Quan hệ vuông góc trong không gian - Đề số 2
