Bài 7 trang 99 SGK Hình học 10
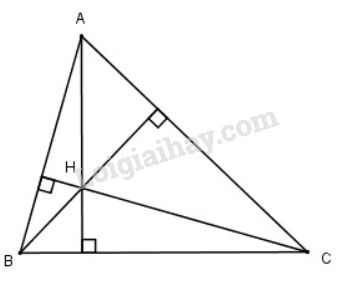
Cho tam giác ABC với H là trực tâm. Biết phương trình của đường thẳng AB, BH và AH lần lượt là: 4x + y – 12 = 0, 5x – 4y – 15 = 0 và 2x + 2y – 9 = 0
Đề bài
Cho tam giác \(ABC\) với \(H\) là trực tâm. Biết phương trình của đường thẳng \(AB, BH\) và \(AH\) lần lượt là: \(4x + y – 12 = 0, 5x – 4y – 15 = 0\) và \(2x + 2y – 9 = 0\)
Hãy viết phương trình hai đường thẳng chứa hai cạnh còn lại và đường cao thứ ba.
Video hướng dẫn giải
Lời giải chi tiết
\(A = AH \cap AB\) nên tọa độ đỉnh \(A\) là nghiệm của hệ:
\(\left\{ \matrix{
4x + y - 12 = 0 \hfill \cr
2x + 2y - 9 = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = \dfrac{5}{2}\\
y = 2
\end{array} \right.\)
\( \Rightarrow A({5 \over 2},2)\)
\(BH : 5x – 4y – 15 = 0\) \( \Rightarrow \overrightarrow {{n_{BH}}} = \left( {5; - 4} \right) \Rightarrow \overrightarrow {{u_{BH}}} = \left( {4;5} \right)\)
\(AC \bot BH \Rightarrow AC\) nhận \(\overrightarrow {{u_{BH}}} = \left( {4;5} \right)\) làm một vecto pháp tuyến.
Mà \(AC\) đi qua \(A({5 \over 2},2)\) nên \(AC:4.(x - {5 \over 2}) + 5(y - 2) = 0 \)\(\Leftrightarrow 4x + 5y - 20 = 0\)
\(B = AB \cap BH\) nên tọa độ đỉnh \(B\) là nghiệm của hệ:
\(\left\{ \matrix{
4x + y - 12 = 0 \hfill \cr
6x - 4y - 15 = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = 3\\
y = 0
\end{array} \right.\)
\( \Rightarrow B(3,0)\)
\(AH: 2x + 2y – 9 = 0\) có \(\overrightarrow {{n_{AH}}} = \left( {2;2} \right) \Rightarrow \overrightarrow {{u_{AH}}} = \left( {1; - 1} \right)\) là VTCP.
\(BC \bot AH\) nên nhận \(\overrightarrow {{u_{AH}}} = \left( {1; - 1} \right)\) làm VTPT
\( \Rightarrow BC:- 1(x - 3) + (y - 0) = 0 \)\(\Leftrightarrow x - y - 3 = 0\)
\(H = BH \cap AH\) nên tọa độ \(H\) là nghiệm của hệ phương trình:
\(\left\{ \matrix{
5x - 4y - 15 = 0 \hfill \cr
2x + 2y - 9 = 0 \hfill \cr} \right.\)
\( \Leftrightarrow \left\{ \begin{array}{l}
x = \dfrac{{11}}{3}\\
y = \dfrac{5}{6}
\end{array} \right. \Rightarrow H\left( {\dfrac{{11}}{3};\dfrac{5}{6}} \right)\)
\(AB:4x + y - 12 = 0\) \(\Rightarrow \overrightarrow {{n_{AB}}} = \left( {4;1} \right) \Rightarrow \overrightarrow {{u_{AB}}} = \left( {1; - 4} \right)\) là VTCP của \(AB\).
\(CH \bot AB \Rightarrow \overrightarrow {{n_{CH}}} = \overrightarrow {{u_{AB}}} = \left( {1; - 4} \right)\) là VTPT của \(CH\).
Mà \(CH\) đi qua \(H\) nên:
\(CH:1\left( {x - \dfrac{{11}}{3}} \right) - 4\left( {y - \dfrac{5}{6}} \right) = 0 \) \(\Leftrightarrow x - 4y - \dfrac{1}{3} = 0\) \( \Leftrightarrow 3x - 12y - 1 = 0\)
Vậy: \(AC: 4x + 5y - 20 = 0\)
\( BC:x - y - 3 = 0\)
\(CH: 3x - 12y - 1 = 0\)
Loigiaihay.com
Bình luận
Chia sẻ
- Bài 8 trang 99 SGK Hình học 10
- Bài 9 trang 99 SGK Hình học 10
- Bài 6 trang 99 SGK Hình học 10
- Bài 5 trang 99 SGK Hình học 10
- Bài 4 trang 99 SGK Hình học 10
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 10 - Xem ngay
PH/HS Tham Gia Nhóm Lớp 10 Để Trao Đổi Tài Liệu, Học Tập Miễn Phí!
