Bài 2 trang 98 SGK Hình học 10
Cho tam giác ABC có hai điểm M,N sao cho
Video hướng dẫn giải
Cho tam giác \(ABC\) có hai điểm \(M,N\) sao cho
\(\left\{ \matrix{
\overrightarrow {AM} = \alpha \overrightarrow {AB} \hfill \cr
\overrightarrow {AN} = \beta \overrightarrow {AC} \hfill \cr} \right.\)
LG a
Hãy vẽ \(\displaystyle M, N\) khi \(\displaystyle \alpha = {2 \over 3};\beta = - {2 \over 3}\)
Lời giải chi tiết:
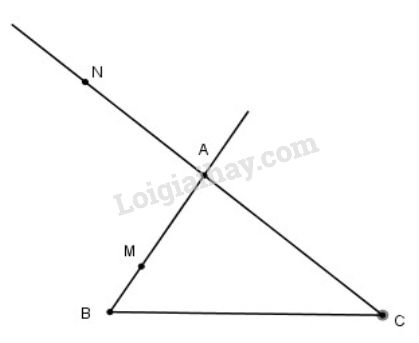
Ta có:
\(\eqalign{
& \overrightarrow {AM} = {2 \over 3}\overrightarrow {AB} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AM} \uparrow \uparrow \overrightarrow {AB} \hfill \cr
AM = {2 \over 3}AB \hfill \cr} \right. \cr
& \overrightarrow {AN} = - {2 \over 3}\overrightarrow {AC} \Leftrightarrow \left\{ \matrix{
\overrightarrow {AN} \uparrow \downarrow \overrightarrow {AC} \hfill \cr
AN = {2 \over 3}AC \hfill \cr} \right. \cr} \)
Vậy \(M\) thuộc đoạn \(AB\) sao cho \(AM = {2 \over 3}AB \) và \(N\) thuộc tia đối của tia \(AC\) sao cho \(AN = {2 \over 3}AC .\)
LG b
Hãy tìm mối liên hệ giữa \(α, β\) để \(MN//BC\)
Lời giải chi tiết:
Ta có:
\(\begin{array}{l}
\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \beta \overrightarrow {AC} - \alpha \overrightarrow {AB} \\
\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \\
MN//BC \Leftrightarrow \dfrac{\beta }{1} = \dfrac{{ - \alpha }}{{ - 1}} \Leftrightarrow \beta = \alpha
\end{array}\)
Vậy \(MN//BC \Leftrightarrow \beta = \alpha .\)
Loigiaihay.com













Danh sách bình luận