Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức:
\(C(v) = \frac{{16000}}{v} + \frac{5}{2}v\) \(\left( {0 < v \le 120} \right)\)
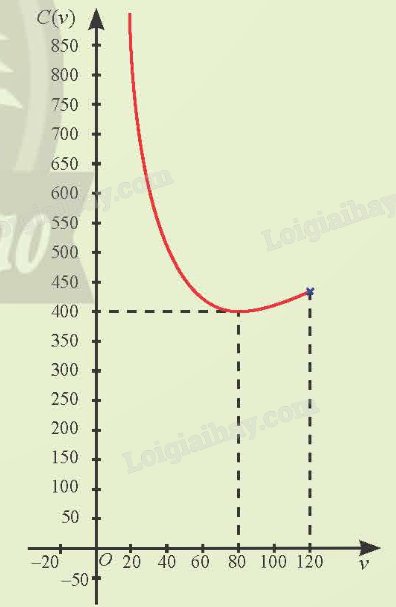
Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C = C(v) như hình bên. Làm thế nào để vẽ được đồ thị hàm số này?
Thực hiện từng bước khảo sát hàm số.
Khảo sát và vẽ đồ thị hàm số C = C(v):
– Tập xác định: D = (0; 120].
– Sự biến thiên:
+ Chiều biến thiên:
Đạo hàm \(C'(v) = - \frac{{16000}}{{{v^2}}} + \frac{5}{2} = \frac{{5(v - 80)(v + 80)}}{{2{v^2}}}\);
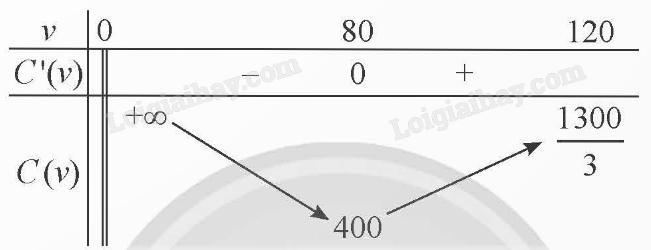
\(C'(v) = 0 \Leftrightarrow \) v = -80 (loại) hoặc v = 80.
Trên khoảng (0;80), C’(v) < 0 nên hàm số nghịch biến trên khoảng này.
Trên khoảng (80;120), C’(v) > 0 nên hàm số đồng biến trên khoảng này.
+ Cực trị: Hàm số đạt cực tiểu tại v = 80, \({C_{CT}} = C(80) = 400\).
+ Giới hạn vô cực và tiệm cận:\(\mathop {\lim }\limits_{x \to {0^ + }} C(v) = \mathop {\lim }\limits_{x \to {0^ + }} \left( {\frac{{16000}}{v} + \frac{5}{2}v} \right) = + \infty \) nên đường thẳng v = 0 là tiệm cận đứng của đồ thị hàm số.
+ Bảng biến thiên:
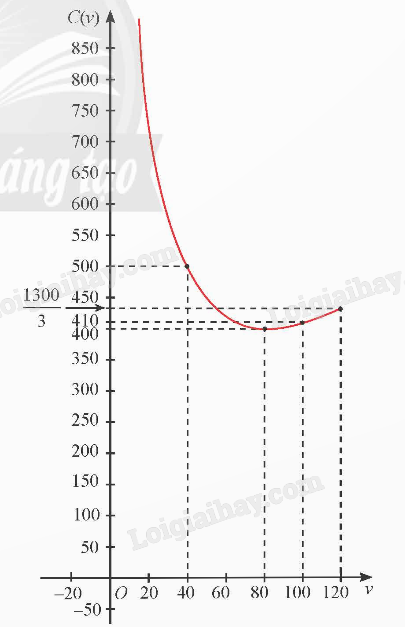
- Đồ thị: Đồ thị hàm số có điểm cực tiểu (80; 400) và đi qua các điểm (40; 500), (100; 410), \(\left( {120;\frac{{1300}}{3}} \right)\).
Các bài tập cùng chuyên đề
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\).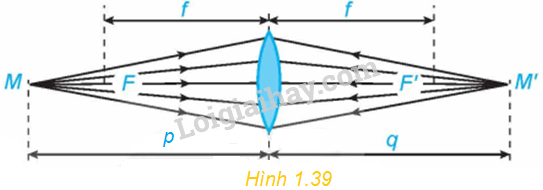
a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\).
b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này.
Lập bảng biến thiên của hàm số \(q = g\left( p \right)\) trên khoảng \(\left( {f; + \infty } \right)\).
Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x - 3\).
Cho hàm số \(y = - {x^2} + 4x - 3\)
a) Lập bảng biến thiên.
b) Vẽ đồ thị của hàm số.
Cho hàm số \(f(x) = 2\cos x + x\).
a) \(f(0) = 2;f\left( {\frac{\pi }{2}} \right) = \frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là\({f^\prime }(x) = 2\sin x + 1\).
c) Nghiệm của phương trình \({f^\prime }(x) = 0\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\) là \(\frac{\pi }{6}\).
d) Giá trị lớn nhất của \(f(x)\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\) là \(\sqrt 3 {\rm{\;}} + \frac{\pi }{6}\).
Cho hàm số \(f(x) = 5x - {\log _3}(x + 1)\).
a) Hàm số f(x) nghịch biến trên khoảng (1;0) .
b) Hàm số f(x) có một điểm cực đại.
c) Đạo hàm của hàm số f(x) là \(f'(x) = 5 - \frac{1}{{(x + 1)\ln 3}}\), \(\forall x \in ( - 1; + \infty )\).
d) Giá trị của hàm số f(x) tại điểm x = 2 là f(2) = 9.
Cho hàm số f(x) = 4sinx + 2x + 1.
a) \(f(0) = 1\); \(f\left( { - \frac{\pi }{2}} \right) = - \pi - 3\).
b) Đạo hàm của hàm số đã cho là f’(x) = -4cosx + 2.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \([0;\pi ]\) là \(\frac{{2\pi }}{3}\).
d) Giá trị lớn nhất của f(x) trên đoạn \([0;\pi ]\) là \(2\pi + 1\).
Cho hàm số \(f(x) = \ln x - \frac{x}{2}\).
a) Tập xác định của hàm số là \(D = (0; + \infty )\).
b) \(f(1) = - \frac{1}{2}\); \(f(e) = - \frac{e}{2}\).
c) Nghiệm của phương trình \(f'(x) = 0\) trên đoạn [1;e] là x = 2.
d) Giá trị lớn nhất của hàm số f(x) trên đoạn [1;e] bằng \( - \frac{1}{2}\).
Cho hàm số \(y = {x^3} - 3{x^2} + 4\).
a) Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số y = f(x). Khi đó độ dài AB bằng \(\sqrt 5 \).
d) Đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng.
Cho hàm số \(f\left( x \right) = {e^{2x}} - 2x\).
a) Hàm số có tập xác định là R.
b) Đạo hàm của hàm số đã cho là \(f'\left( x \right) = 2{e^{2x}} - 2\).
c) Tập nghiệm của bất phương trình \(f'\left( x \right) > 0\) là \(S = \left( {0; + \infty } \right)\).
d) Hàm số đã cho có giá trị cực tiểu bằng 0.
