Cho hàm số \(f\left( x \right) = {e^{2x}} - 2x\).
a) Hàm số có tập xác định là R.
b) Đạo hàm của hàm số đã cho là \(f'\left( x \right) = 2{e^{2x}} - 2\).
c) Tập nghiệm của bất phương trình \(f'\left( x \right) > 0\) là \(S = \left( {0; + \infty } \right)\).
d) Hàm số đã cho có giá trị cực tiểu bằng 0.
a) Hàm số có tập xác định là R.
b) Đạo hàm của hàm số đã cho là \(f'\left( x \right) = 2{e^{2x}} - 2\).
c) Tập nghiệm của bất phương trình \(f'\left( x \right) > 0\) là \(S = \left( {0; + \infty } \right)\).
d) Hàm số đã cho có giá trị cực tiểu bằng 0.
Tìm tập xác định của hàm số \(f(x)\).
Tính đạo hàm f’(x) của hàm số \(f(x)\).
Lập bảng biến thiên rồi kết luận giá trị cực tiểu của hàm số.
a) Đúng. Hàm số đã cho có tập xác định là \(\mathbb{R}\).
b) Đúng. \(f'(x) = \left( {2{e^{2x}} - 2x} \right)' = 2{e^{2x}} - 2\).
c) Đúng. \(f'(x) > 0 \Leftrightarrow 2{e^{2x}} - 2 > 0 \Leftrightarrow {e^{2x}} > 1 \Leftrightarrow 2x > 0 \Leftrightarrow x > 0\).
Vậy tập nghiệm của bất phương trình là \(S = \left( {0; + \infty } \right)\).
d) Sai. Ta có \(f'(x) = 0 \Leftrightarrow x > 0\).
Bảng biến thiên:
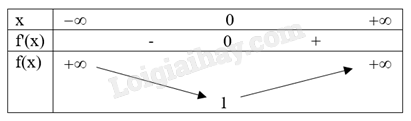
Hàm số đã cho có giá trị cực tiểu bằng 1.

Các bài tập cùng chuyên đề
Xét một thấu kính hội tụ có tiêu cự f (H.1.39). Khoảng cách p từ vật đến thấu kính liên hệ với khoảng cách q từ ảnh đến thấu kính bởi hệ thức: \(\frac{1}{p} + \frac{1}{q} = \frac{1}{f}\).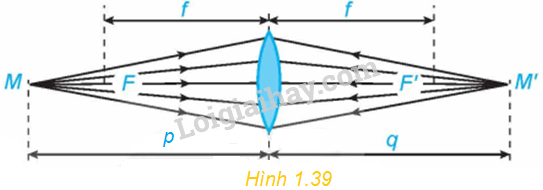
a) Viết công thức tính \(q = g\left( p \right)\) như một hàm số của biến \(p \in \left( {f; + \infty } \right)\).
b) Tính các giới hạn \(\mathop {\lim }\limits_{p \to + \infty } g\left( p \right),\mathop {\lim }\limits_{p \to {f^ + }} g\left( p \right)\) và giải thích ý nghĩa các kết quả này.
Lập bảng biến thiên của hàm số \(q = g\left( p \right)\) trên khoảng \(\left( {f; + \infty } \right)\).
Lập bảng biến thiên và vẽ đồ thị của hàm số \(y = {x^2} - 2x - 3\).
Cho hàm số \(y = - {x^2} + 4x - 3\)
a) Lập bảng biến thiên.
b) Vẽ đồ thị của hàm số.
Cho hàm số \(f(x) = 2\cos x + x\).
a) \(f(0) = 2;f\left( {\frac{\pi }{2}} \right) = \frac{\pi }{2}\).
b) Đạo hàm của hàm số đã cho là \({f^\prime }(x) = 2\sin x + 1\).
c) Nghiệm của phương trình \({f^\prime }(x) = 0\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\) là \(\frac{\pi }{6}\).
d) Giá trị lớn nhất của \(f(x)\) trên đoạn \(\left[ {0;\frac{\pi }{2}} \right]\) là \(\sqrt 3 {\rm{\;}} + \frac{\pi }{6}\).
Cho hàm số \(f(x) = 5x - {\log _3}(x + 1)\).
a) Hàm số f(x) nghịch biến trên khoảng (1;0) .
b) Hàm số f(x) có một điểm cực đại.
c) Đạo hàm của hàm số f(x) là \(f'(x) = 5 - \frac{1}{{(x + 1)\ln 3}}\), \(\forall x \in ( - 1; + \infty )\).
d) Giá trị của hàm số f(x) tại điểm x = 2 là f(2) = 9.
Cho hàm số f(x) = 4sinx + 2x + 1.
a) \(f(0) = 1\); \(f\left( { - \frac{\pi }{2}} \right) = - \pi - 3\).
b) Đạo hàm của hàm số đã cho là f’(x) = -4cosx + 2.
c) Nghiệm của phương trình f’(x) = 0 trên đoạn \([0;\pi ]\) là \(\frac{{2\pi }}{3}\).
d) Giá trị lớn nhất của f(x) trên đoạn \([0;\pi ]\) là \(2\pi + 1\).
Cho hàm số \(f(x) = \ln x - \frac{x}{2}\).
a) Tập xác định của hàm số là \(D = (0; + \infty )\).
b) \(f(1) = - \frac{1}{2}\); \(f(e) = - \frac{e}{2}\).
c) Nghiệm của phương trình \(f'(x) = 0\) trên đoạn [1;e] là x = 2.
d) Giá trị lớn nhất của hàm số f(x) trên đoạn [1;e] bằng \( - \frac{1}{2}\).
Cho hàm số \(y = {x^3} - 3{x^2} + 4\).
a) Hàm số y = f(x) nghịch biến trên khoảng (0;2).
b) Giới hạn \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty \).
c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số y = f(x). Khi đó độ dài AB bằng \(\sqrt 5 \).
d) Đồ thị hàm số \(y = \frac{{x + 1}}{{f(x)}}\) có đúng hai đường tiệm cận đứng.
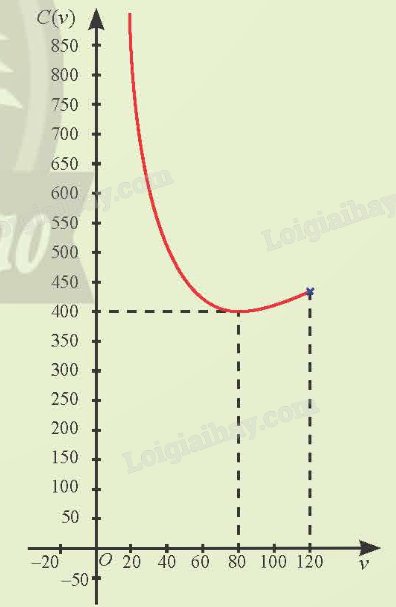
Giả sử chi phí tiền xăng C (đồng) phụ thuộc tốc độ trung bình v (km/h) theo công thức:
\(C(v) = \frac{{16000}}{v} + \frac{5}{2}v\) \(\left( {0 < v \le 120} \right)\)
Để biểu diễn trực quan sự thay đổi của C(v) theo v, người ta đã vẽ đồ thị hàm số C = C(v) như hình bên. Làm thế nào để vẽ được đồ thị hàm số này?
Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = ax + b theo sơ đồ trên.
Khảo sát sự biến thiên và vẽ đồ thị của hàm số \(y = ax^2 + bx + c\) theo sơ đồ trên.







Danh sách bình luận