Toán 11, giải toán lớp 11 cánh diều Bài tập cuối chương VIII Toán 11 Cánh Diều

Bài 6 trang 116 SGK Toán 11 tập 2 - Cánh Diều


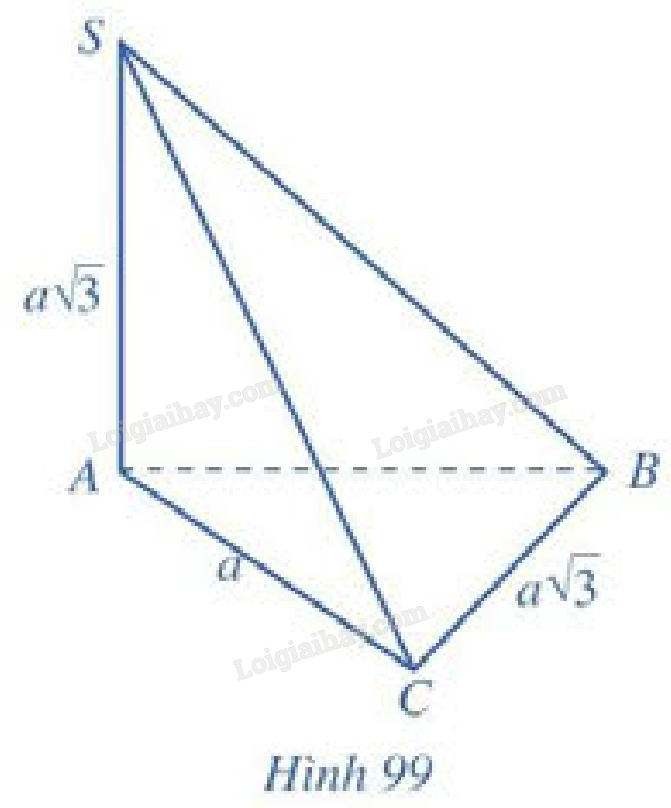
Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AC \bot BC,\)\(SA = BC = a\sqrt 3 ,AC = a\)(Hình 99).

Đề bài

Cho hình chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right),AC \bot BC,\)\(SA = BC = a\sqrt 3 ,AC = a\)(Hình 99).

a) Tính góc giữa hai đường thẳng \(SA\) và \(BC\).

b) Tính góc giữa đường thẳng \(SC\) và mặt phẳng \(\left( {ABC} \right)\).

c) Tính số đo của góc nhị diện \(\left[ {B,SA,C} \right]\).

d) Tính khoảng cách từ \(B\) đến mặt phẳng \(\left( {SAC} \right)\).

e) Tính khoảng cách giữa hai đường thẳng \(SA\) và \(BC\).

g) Tính thể tích của khối chóp \(S.ABC\).

Phương pháp giải - Xem chi tiết

a) Cách xác định góc giữa hai đường thẳng \(a\) và \(b\):

Bước 1: Lấy một điểm \(O\) bất kì.

Bước 2: Qua điểm \(O\) dựng đường thẳng \(a'\parallel a\) và đường thẳng \(b'\parallel b\).

Bước 3: Tính \(\left( {a,b} \right) = \left( {a',b'} \right)\).

b) Cách tính góc giữa đường thẳng và mặt phẳng: Tính góc giữa đường thẳng đó và hình chiếu của nó lên mặt phẳng.

c) Cách xác định góc nhị diện \(\left[ {{P_1},d,{Q_1}} \right]\)

Bước 1: Xác định \(c = \left( {{P_1}} \right) \cap \left( {{Q_1}} \right)\).

Bước 2: Tìm mặt phẳng \(\left( R \right) \bot c\).

Bước 3: Tìm \(p = \left( R \right) \cap \left( {{P_1}} \right),q = \left( R \right) \cap \left( {{Q_1}} \right),O = p \cap q,M \in p,N \in q\).

Khi đó \(\left[ {{P_1},d,{Q_1}} \right] = \widehat {MON}\).

d) Cách tính khoảng cách từ một điểm đến một mặt phẳng: Tính khoảng cách từ điểm đó đến hình chiếu của nó lên mặt phẳng.

e) Cách tính khoảng cách giữa hai đường thẳng chéo nhau:

Cách 1: Dựng đường vuông góc chung.

Cách 2: Tính khoảng cách từ đường thẳng này đến một mặt phẳng song song với đường thẳng đó và chứa đường thẳng còn lại.

g) Sử dụng công thức tính thể tích khối chóp: \(V = \frac{1}{3}Sh\).

Lời giải chi tiết

a) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC \Rightarrow \left( {SA,BC} \right) = {90^ \circ }\).

b) \(SA \bot \left( {ABC} \right) \Rightarrow \left( {SC,\left( {ABC} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)

\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3  \Rightarrow \widehat {SCA} = {60^ \circ }\)

Vậy \(\left( {SC,\left( {ABC} \right)} \right) = {60^ \circ }\).

c) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AB,SA \bot AC\)

Vậy \(\widehat {BAC}\) là góc nhị diện \(\left[ {B,SA,C} \right]\).

\(\Delta ABC\) vuông tại \(C \Rightarrow \tan \widehat {BAC} = \frac{{BC}}{{AC}} = \frac{{a\sqrt 3 }}{a} = \sqrt 3  \Rightarrow \widehat {BAC} = {60^ \circ }\).

d)

\(\begin{array}{l}\left. \begin{array}{l}SA \bot \left( {ABC} \right) \Rightarrow SA \bot BC\\AC \bot BC\end{array} \right\} \Rightarrow BC \bot \left( {SAC} \right)\\ \Rightarrow d\left( {B,\left( {SAC} \right)} \right) = BC = a\sqrt 3 \end{array}\)

e) \(SA \bot \left( {ABC} \right) \Rightarrow SA \bot AC,AC \bot BC\)

\( \Rightarrow d\left( {SA,BC} \right) = AC = a\)

g) \({S_{\Delta ABC}} = \frac{1}{2}AC.BC = \frac{1}{2}a.a\sqrt 3  = \frac{{{a^2}\sqrt 3 }}{2}\)

\(\begin{array}{l}h = SA = a\sqrt 3 \\ \Rightarrow {V_{S.ABC}} = \frac{1}{3}.{S_{\Delta ABC}}.SA = \frac{1}{3}.\frac{{{a^2}\sqrt 3 }}{2}.a\sqrt 3  = \frac{{{a^3}}}{2}\end{array}\)


Bình chọn:
4.9 trên 7 phiếu
Bài tiếp theo

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 11 - Cánh diều - Xem ngay

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K8 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store