 Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
Toán lớp 6 - Giải toán lớp 6 Kết nối tri thức, Cánh diều, Chân trời sáng tạo
 Bài 8. Tính chất cơ bản của phép cộng phân số
Bài 8. Tính chất cơ bản của phép cộng phân số
Bài 48 trang 28 SGK Toán 6 tập 2
Đố : Cắt một tấm bìa hình tròn bán kính 2,5cm thành 4 phần không bằng nhau như hình 8. Đố em đặt các miếng bìa đã cắt cạnh nhau để...
Đề bài
Đố : Cắt một tấm bìa hình tròn bán kính 2,5cm thành 4 phần không bằng nhau như hình 8.
Đố em đặt các miếng bìa đã cắt cạnh nhau để được:
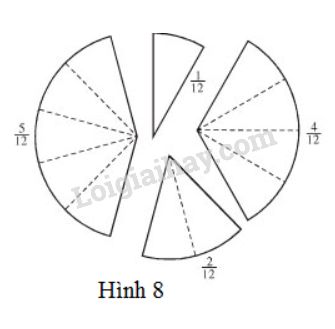
a) \(\dfrac{1}{4}\) hình tròn ;
b) \(\dfrac{1}{2}\) hình tròn ;
c) \(\dfrac{7}{12},\dfrac{2}{3},\dfrac{3}{4},\dfrac{5}{6},\dfrac{11}{12}\) và \(\dfrac{12}{12}\) hình tròn.
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Ghép các phần sao cho tổng của chúng bằng phân số cần tìm.
Lời giải chi tiết
Ghép các miếng bìa như sau:
a) Ta đặt hai miếng bìa \(\dfrac{1}{12}\) và \(\dfrac{2}{12}\) cạnh nhau để được \(\dfrac{1}{4}\) hình tròn.
Vì \(\dfrac{1}{12}+\dfrac{2}{12}=\dfrac{3}{12}=\dfrac{1}{4}.\)
b) Ta đặt hai miếng bìa \(\dfrac{1}{12}\) và \(\dfrac{5}{12}\) cạnh nhau để được \(\dfrac{1}{2}\) hình tròn.
Vì \(\dfrac{1}{12}+\dfrac{5}{12}=\dfrac{6}{12}=\dfrac{1}{2}.\)
Hoặc ta đặt hai miếng bìa \(\dfrac{4}{12}\) và \(\dfrac{2}{12}\) cạnh nhau để được \(\dfrac{1}{2}\) hình tròn.
Vì \(\dfrac{4}{12}+\dfrac{2}{12}=\dfrac{6}{12}=\dfrac{1}{2}.\)
c) Tương tự, từ các phép tính dưới đây ta sẽ suy ra các miếng bìa đặt cạnh nhau để thỏa mãn đề bài.
\(\dfrac{5}{12}+\dfrac{2}{12}=\dfrac{7}{12};\)
\(\dfrac{5}{12}+\dfrac{2}{12}+\dfrac{1}{12}=\dfrac{8}{12}=\dfrac{2}{3};\)
\(\dfrac{5}{12}+\dfrac{4}{12}=\dfrac{9}{12}=\dfrac{3}{4};\)
\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{1}{12}=\dfrac{10}{12}=\dfrac{5}{6};\)
\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{2}{12}=\dfrac{11}{12};\)
\(\dfrac{5}{12}+\dfrac{4}{12}+\dfrac{2}{12}+\dfrac{1}{12}=\dfrac{12}{12}.\)
Loigiaihay.com
Các bài khác cùng chuyên mục












Danh sách bình luận