 Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
Toán 11, giải toán lớp 11 kết nối tri thức với cuộc sống
 Bài 10. Đường thẳng và mặt phẳng trong không gian Toán ..
Bài 10. Đường thẳng và mặt phẳng trong không gian Toán ..
Bài 4.4 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
Đề bài
Cho hình chóp tứ giác S.ABCD và M là một điểm thuộc cạnh SC (M khác S, C). Giả sử hai đường thẳng AB và CD cắt nhau tại N. Chứng minh rằng đường thẳng MN là giao tuyến của hai mặt phẳng (ABM) và (SCD).
Video hướng dẫn giải
Phương pháp giải - Xem chi tiết
Để chứng minh giao tuyến của hai mặt phẳng, ta tìm hai điểm cùng thuộc cả hai mặt phẳng đó.
Lời giải chi tiết
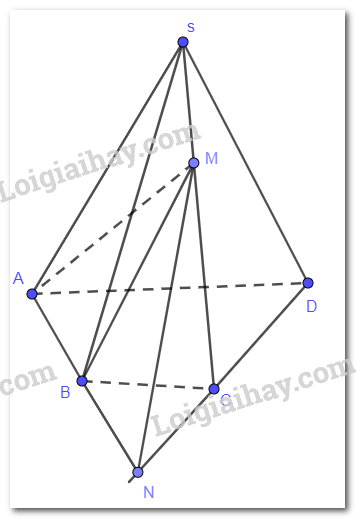
Ta có N thuộc đường thẳng AB , mà AB nằm trong mặt phẳng (ABM) nên N cũng nằm trong mp(ABM).
M và N đều nằm trong mặt phẳng (ABM) nên MN nằm trong mp(ABM) (1)
M thuộc SC suy ra M nằm trong mp(SCD), N thuộc đường thẳng CD nên N nằm trong mp(SCD).
Do đó, MN nằm trong mp(SCD) (2)
Từ (1) và (2) suy ra MN là giao tuyến của hai mp(ABM) và (SCD).
- Bài 4.5 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.6 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.7 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.8 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
- Bài 4.3 trang 77 SGK Toán 11 tập 1 - Kết nối tri thức
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 11 - Kết nối tri thức - Xem ngay
Các bài khác cùng chuyên mục
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 119 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 111 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 95 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 88 SGK Toán 11 tập 1 - Kết nối tri thức
- Giải câu hỏi mở đầu trang 84 SGK Toán 11 tập 1 - Kết nối tri thức












Danh sách bình luận