Giải toán 7, giải bài tập toán lớp 7 sgk đầy đủ đại số và hình học Bài 8. Cộng, trừ đa thức một biến

Bài 44 trang 45 SGK Toán 7 tập 2


Đề bài

Cho hai đa thức: \(P(x) =  - 5{x^3} - \dfrac{1}{3} + 8{x^4} + {x^2}\)
và \(Q(x) = {x^2} - 5x - 2{x^3} + {x^4} - \dfrac{2}{3}\).

Hãy tính \(P(x) + Q(x)\) và \(P(x) - Q(x)\).

Video hướng dẫn giải

Phương pháp giải - Xem chi tiết

Sắp xếp hai đa thức theo lũy thừa giảm dần của biến rồi sau đó thực hiện phép tính cộng hoặc phép tính trừ theo hàng dọc.

Lời giải chi tiết

Cách 1:

Ta sắp xếp hai đa thức theo lũy thừa giảm dần của biến như sau:

\(P(x) = 8{x^4} - 5{x^3} + {x^2} - \dfrac{1}{3}\) ; 

\(Q(x) = {x^4} - 2{x^3} + {x^2} - 5x - \dfrac{2}{3}\).

Thực hiện phép tính ta có:

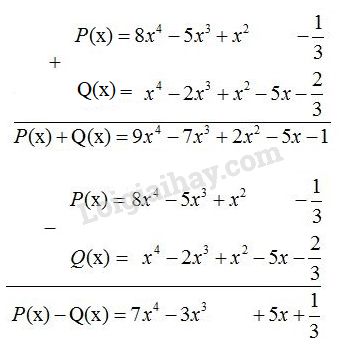
Cách 2:

\(P(x)+Q(x) = 8{x^4} - 5{x^3} + {x^2} - \dfrac{1}{3}+ {x^4} - 2{x^3} + {x^2} - 5x - \dfrac{2}{3}\\=( 8{x^4}+x^4) +[( - 5{x^3})+ (- 2{x^3})] + ( {x^2} + {x^2} )+[(- \dfrac{1}{3})+( - \dfrac{2}{3})]\\=9x^4 - 7x^3 + 2x^2-5x-1\)

\(P(x)-Q(x) = 8{x^4} - 5{x^3} + {x^2} - \dfrac{1}{3}-( {x^4} - 2{x^3} + {x^2} - 5x - \dfrac{2}{3})\\= 8{x^4} - 5{x^3} + {x^2} - \dfrac{1}{3}- {x^4} + 2{x^3} - {x^2} +5x + \dfrac{2}{3}\\=( 8{x^4}-x^4) +[( - 5{x^3})+ 2{x^3}]+ ( {x^2} - {x^2} )+[(- \dfrac{1}{3})+\dfrac{2}{3}]\\=7x^4 - 3x^3 +5x+\dfrac{1}{3}\)


Bình chọn:
4.3 trên 381 phiếu
Bài tiếp theo

>> Xem thêm

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K11 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 7 trên Tuyensinh247.com cam kết giúp học sinh lớp 7 học tốt, hoàn trả học phí nếu học không hiệu quả.

Các bài khác cùng chuyên mục


App Loigiaihay trên google play store App Loigiaihay trên apple store

Copyright © 2021 loigiaihay.com

DMCA.com Protection Status
App Loigiaihay trên apple store App Loigiaihay trên google play store

Đăng ký để nhận lời giải hay và tài liệu miễn phí

Cho phép loigiaihay.com gửi các thông báo đến bạn để nhận được các lời giải hay cũng như tài liệu miễn phí.

Đồng ý Bỏ qua